8.5. Связь между местной, средней и максимальной скоростями в трубах

Установим связи между местной, средней и максимальной осредненными скоростями при турбулентном режиме движения жидкости в трубе в виде безразмерных отношений ,,. Такие выражения называются относительными дефицитами скорости.

Относительный дефицит местной скорости от максимальной определим, найдя сначалаиз (8.23) при.

Тогда

. (8,24)

Перейдя к десятичным логарифмам, получим

или

,

где .

При , тогда

.

Относительный дефицит средней скорости от максимальной. Найдем расход в круглой трубе, записав его сначала в виде расхода через кольцо толщиной , отстоящее от оси на расстоянии,, а затем проинтегрировав по площади живого сечения:

.

Заменяя и интегрируя от 0 до, т.е. по всему сечению, подставив из (8.24)

,

получим

.

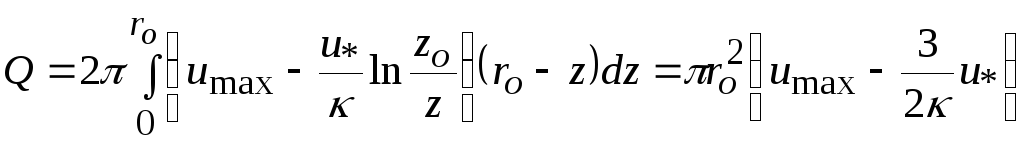Тогда

.

При постоянном значении величина 3/2также является постоянной и обозначается.

Относительный дефицит средней скорости от максимальной - постоянная величина, равная

. (8.25)

Относительная максимальная скорость определяется как

или с учетом (7.24), где ,

.

Относительный дефицит местной скорости от средней найдем, использовав полученное по (8.25) и подставив это выражение в .(8 24):

.

При = 0,4 имеем=3,75 и

.

Для того чтобы найти относительную местную скорость , преобразуем

и получим

.

Подставляя по (7 24) , получаем

.

Приняв, как и ранее, =0,4, получим

. (8.26)

На оси трубы

.

При (8.26) принимает вид

,

где - расстояние от стенки трубы до точки, в которой. Поскольку, то.

Опыты Ф. А. Шевелева показали, что в трубопроводах промышленного изготовления расстояние до точки, где местная скорость равна средней скорости, , в трубах из гидрофобного материала расстояние до точки, где, меньше.

Коэффициенты кинетической энергии (коэффициент Кориолиса) и количества движения (коэффициент Буссинеска)для турбулентного движения. Из выражений соответственно (5 16) и (5 28)

;

с учетом (8.26) при =0,4 и3,75 были получены уравнения

;

.

Для , найденного из(=9,81 м/с²), эти уравнения имеют вид

;

.

8.6. Гидравлически гладкие и шероховатые трубы (русла). Толщина вязкого подслоя

Шероховатость поверхности водотоков (труб, каналов и т. д.) может быть различной. Если поверхность труб и открытых лотков покрывается специально отсортированными зернами песка одной фракции, то получается равнозернистая шероховатость (рис. 8.4, а). Она используется только в лабораторных исследованиях.

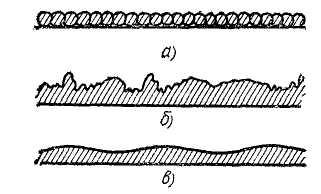
Рис.8.4

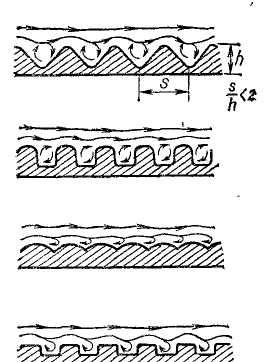
Рис.8.5

Поверхность труб и открытых водотоков обычно неравнозернистая, она может быть волнистой с различными высотами и длинами волн (или микроволн) (рис. 8.4, б, в).

В трубах помимо выступов с неодинаковыми размерами и формой может быть и регулярная шероховатость, обусловленная технологией изготовления и назначением труб (например, гофрированные трубы, рис. 8.5).

Рис.8.6

Синтетические гофрированные дренажные трубы различаются по очертаниям гофров и относительному расстоянию между вершинами гофров (рис. 8.5). В синтетических негофрированных трубах отношение длины микроволн к их высоте составляет от 15 до 35.

В водотоках, проходящих в песчаных несвязных грунтах, на дне (иногда и на откосах) образуются различные формы рельефа (гряды - более крупные образования, рифели - более мелкие, рис. 8.6). Поверхность этих форм покрыта зернами песка.

Могут быть и другие виды шероховатости с выступами различных размеров по всем трем координатам. Взаимное расположение элементов шероховатости также может быть различным.

Учет конкретных особенностей шероховатости необходим в гидравлических исследованиях и расчетах.

Наиболее полные сведения о шероховатости, о размерах выступов и их взаимном расположении дает статистическое описание.

Понятие о гидравлически гладких и гидравлически шероховатых трубах (руслах). В качестве характеристики шероховатости выбирают некоторую среднюю высоту выступов шероховатости .

Соотношение между высотой выступов идеализированной шероховатости и толщиной вязкого подслояопределяет структуру потока.

Если высота выступов шероховатости меньше, чем толщина вязкого подслоя, то все неровности полностью погружены в этот подслой и жидкость в пределах этого подслоя плавно обтекает выступы шероховатости. В этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости. Такие стенки и трубы (или русла) условно называются гидравлически гладкими (рис. 8.7, с). Если высота выступов шероховатостипревышает толщину вязкого подслоя, то неровности стенок входят в пределы турбулентного ядра, поток обтекает выступы с отрывом, сопровождающимся интенсивным перемешиванием частиц. В этом случае потери напора зависят от шероховатости, и такие трубы (или русла) называются гидравлически шероховатыми (рис. 8.7,б). В третьем случае, являющемся промежуточным между двумя вышеуказанными, абсолютная высота выступов шероховатости примерно равна толщине вязкого подслоя.

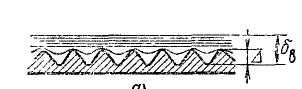
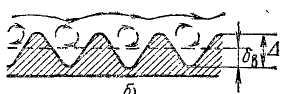
Рис.8.7

Толщина вязкого подслоя. Так как толщина вязкого подслоя мала, то градиент скорости в этом подслое можно принять равным(-осредненная продольная составляющая скорости на внешней границе вязкого подслоя). Тогда касательное напряжение на стенке трубы равно

или

. (8.27)

Так как по (7.30) , то из (8.27) найдем

.

Отсюда

. (8.28)

В (8.28) обе части - безразмерные. В левой части - безразмерный комплекс , аналогичный по структуре числу Рейнольдса и обычно обозначаемый символом. Приближенно можно считать, чтовеличина постоянная. Тогда из (8.28) имеем

(8.29)

Из (8.29) получим значение скорости на внешней границе вязкого подслоя

(8.30)

и толщину вязкого подслоя

. (8.31)

Экспериментально найдено, что .

Найдем расчетную формулу для толщины вязкого подслоя . Для этого обе части (8.31) разделим на диаметр трубыи преобразуем:

(8.32)

Подставив в (8.32) выражение относительной средней скорости (7.24) , получим

.

Окончательно толщину вязкого подслоя найдем в виде

. (8.33)

Таким образом, с ростом числа Re, а также коэффициента Дарси толщина вязкого подслояуменьшается.

Исследования структуры потока вблизи стенки трубы, выполнявшиеся с помощью совершенной аппаратуры, показали, что толщина вязкого подслоя является пульсирующей величиной: значениеизменяется во времени от 2,3 до 18 (среднее значение). Таким образом,изменяется во времени отдо. В практических расчетах это обстоятельство можно не учитывать и приниматьпо (8 33).

Разделение стенок (трубы, русла) на гидравлически гладкие и шероховатые является условным, поскольку, как следует из формулы (8.33), толщина обратно пропорциональна числуRe. Таким образом, при движении жидкости вдоль одной и той же поверхности с неизменной высотой выступа шероховатости в зависимости от числа Рейнольдса толщина вязкого подслоя может изменяться. При увеличении числа Re толщина уменьшается и стенка, бывшая гидравлически гладкой, может стать шероховатой, так как высота выступов шероховатости окажется больше толщины вязкого подслоя и шероховатость станет влиять на характер движения, и следовательно, на потери напора.