1. Порядок выполнения курсовой работы

   1. Общие положения

Курсовая работа «Исследование систем управления методами теории массового обслуживания» является самостоятельной исследовательской работой студента и выполняется под руководством преподавателя.

Выполнение курсовой работы производится на основе индивидуально задания, выдаваемого студенту преподавателем. Пояснительная записка должна включать следующие разделы:

1. Построение статистических распределений;

2. Определение числовых характеристик статистического распределения;

3. Выбор теоретических распределений;

4. Определение необходимого количества управленческого персонала по данным критериям качества.

Графическая часть курсовой работы должна быть выполнена в виде приложений и должна включать эмпирические и теоретические распределения ежесуточного поступления заявок в систему и времени их обслуживания.

1. Последовательность выполнения курсовой работы

1. Для данных вариационных рядов строится многоугольник(полигон) распределения для дискретных случайных величин или гистограмма для непрерывных случайных величин;

2. Определяются числовые характеристики статистических распределений;

3. Решается задача соответствия эмпирических распределений одному из следующих теоретических:

   1. Пуассона ( 1-ая часть индивидуального задания);

   2. Нормальному или показательному (2-ая часть индивидуального задания).

При наличии стандартных программных средств данные 2-ой части задания можно проверить на соответствие логарифмически-нормальному распределению, Вейбулла, Эрланге и другим распределениям.

Задача проверки правдоподобия гипотез решается по критерию Х² . При желании можно решить её по другому критерию, например критерию Колмогорова.

4. Решение задачи синтеза СМО типа М/М/М по заданным критериям качества.

Методологические рекомендации по выполнению курсовой работы

Работа выполняется в следующей последовательности:

1. По статистическим данным строится гистограмма. Следует обратить особое внимание на группировку статистического материала. Число разрядов, на которые следует группировать статистические данные, не должно быть слишком большим, в этом случает ряд становится невыразительным, и в нем обнаруживаются незакономерные колебания. С другой стороны, при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо.

Практика показывает, что число разрядов в большинстве случаев рационально выбирать 10-20, чем однородней статистический материал, тем большее число разрядов следует выбирать. Длины разрядов могут быть как одинаковыми, так и различными. проще, разумеется, их брать одинаковыми, однако статистические данные распределены неравномерно, можно брать интервалы различными. В области большой плотности статистических данных разряды выбираются более узкими. Существует зависимость для определения оптимальной величины интервала, при которой вариационный ряд не будет очень громоздким, и в нем не исчезнут особенности явлений:

где h – величина интервала

xmax и xmin –соответственно максимальное и минимальное значения случайной величины в выборке

n- объем выборки.

В первой части индивидуально задания количество разрядов определяется максимальным значение случайной величины, во второй части достаточно выбрать 6-8 разрядов группировки.

При группировке значений случайной величины по разрядам возникает вопрос, к какому разряду отнести значение, находящееся на границе двух разрядов. В этом случае данное значение можно считать принадлежащим в равной мере к обоим разрядам и прибавлять к количеству значений того т другого разряда 0,5.

При построении гистограммы необходимо частоту каждого разряда разделить на длину интервала и полученное число взять в качестве высоты прямоугольник для данного разряда группировки.

2. .Подбор теоретических распределений по статическим данным.

По внешнему виду гистограммы выбирается ближайшее стандартное теоретическое распределение. Заданное функцией распределение F(x) или вероятностью f(х),выдвигается гипотеза Но о соответствии выбранного теоретического распределения заданному эмпирическому (Эр).

Межу заданными распределениями неизбежны расхождения, которые могут быть вызваны двумя причинами .

2.1 Расхождения случайны, несущественны, вызваны недостаточным количеством данных неудачно выбранным интервалом группировки. В этом случае гипотеза Но принимается.

2.2 Расхождения между теоретическим и эмпирическим распределением существенны ,значимы. Объяснить случайность их нельзя. В этом случае гипотеза не принимается.

Ответ на поставленный вопрос дают критерии согласия, построенные на анализе мер расхождения между теоретическим и эмпирическим распределениями.

В качестве меры расхождения выберем величину w :

W= (1)

Где Pi*-статическая вероятность (частота) I-го разряда;

Pi-теоретическая вероятность ,подсчитанное для i-го разряда по выбранному теоретическому закону распределения ;

Сi-коэффициент ,учитывающий вес для i-го разряда ;

К-число интервалов группировки.

Очевидно, что это есть некоторая случайная величина, закон распределения которого зависит от выбранного теоретического распределения F(х) и числа данных n. Допустим, что этот закон распределения нам известен. В результате эксперимента установлено, что выбранная нами случайная величина w , рассчитанное по выражению (1), получило значение ω.

Спрашивается, можно ли объяснить случайными принципами или же это расхождение слишком велико и указывает на наличие существенной разницы между Тр и Эр распределениями и следовательно на пригодность теории Но ?

Для ответа на этот вопрос предположим, что гипотеза Но верна и вычислим в этом предположении вероятность того, что за счет случайных причин, связанные с недостаточным объемом опытного материала, мера расхождения w не меньше, чем наблюдаемое нами в опыте значение ω , то есть вычислим вероятность события

Р(w≥ ω)

Если это вероятность весьма мала, гипотезу Но следует отвергнуть. Как малоправдоподобную; если не это вероятность значительна, следует признать, что экспериментальные данные не противоречат гипотезе Но.

Осталось ответить на два вопроса:

1. Как выбрать граничное значение вероятности Р(w≥ ω),отделяющее область значений w принятия гипотезы Но от области его опровержения ?

2. Как выбрать закон распределения меры расхождения w?

Очевидно, что если значение ω меры расхождения w , полученное в эксперименте слишком велико , то вероятно , чтобы гипотеза Но подтвердилась .

В качестве маловероятного события выбираем вероятность практически невозможного события , определяемого уровнем значимости.

Наибольшее отличие вероятности события – значение от нуля (единицы), при котором событие можно считать практически невозможным, называется уровнем значимости и обозначается ɑ (альфа) Уровень значимости задается в зависимости от последней ошибки. В экономике чаще всего принимают значение 0,01 и 0,05, если, конечно , ошибки не очень серьезны.

Задавшись значением уровня значимости ɑ, например 0,05,по известному закону w можно найти соответствующее ему значение меры расхождения ω, которое обозначим ω кр.(критическое).

ω кр разделяет область возможных значений меры расхождения w на две части: область принятия гипотезы и критическую область. Для принятия гипотезы полученное в эксперименте значение ω, обозначим его ωр . Допустимо быть ωр< ω кр.

Как выбрать закон распределения меры расхождения W

Оказывается, что при некоторых способах её выбора закон распределения величины W обладает весьма простыми свойствами и при достаточно большом n практически не зависит от выбранного теоретического закона распределения F(x) именно такими методами расхождения и пользуются в качестве критериев согласия.

Одним из часто применяемых критериев согласия является «критерий X²» (читается хи-квадрат) Пирсона.

В выражении 1 коэффициенты С_i («веса разрезов») вводятся потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение P_i * - P_i может быть мало значительным, если сама вероятность P_i велика, и очень заметным, если она мала. Поэтому естественно «веса» С_i взять обратно пропорциональным вероятностям разрезов P_i.

К. Пирсон показал, что если положить

C_i = n/P_i (2)

то при больших n закон распределения величины W обладает весьма простыми свойствами: он практически не зависит от функции распределения F(x) и от числа открытых данных n, а зависит только от числа разрядов группировки k, а именно, этот закон при увеличении n приближается к распределению Х² .

При таком выборе коэффициента С_i мера расхождения обычно обозначается Х²:

Х² = n (3)

Для удобства вычислений (чтобы не иметь дело с дробными величинами, с большим числом нулей) можно ввести nпод знак суммы и учитывая, что

(4)

Где m_i – число значений в i-том разряде. Привести формулу 3 к виду:

W = Х² = (5)

Указанную величину принимаем в качестве критерия проверки гипотезы Но. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия.

Распределение Х² зависит от параметра r, независимого числом степеней свободы распределения. Число степеней связи r разно:

r = k – s – 1

s – число параметров выбранного теоретического распределения F(x).

Для стандартных распределений Пуассона s = 1, для нормального s = 2, для показательного s = 1.

Распределение Х² протабулировано. По таблице для выбранного α и k можно найти х²_кр (α;r),.

Критическая точка выбрана исходя из требования при справедливости нулевой гипотезы вероятность того, что критерий Х² примет значение больше х²_крдолжна быть равна принятому уровню значимости α.

PζX² > х²_кр (α;r)

Таким образом, критическая область критерия определяется неравенством Х²_набл > х²_кр (α;r),а область принятия гипотезы – неравенством Х²_набл < х²_кр (α;r),

Затем по статистическим данным вычисляем наблюдаемое значение критерия Х²_набл.

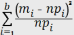
Х²_набл = (6)

Если окажется, что Х²_набл > х²_кр , то нулевую гипотезу Но отвергают, если же Х²_набл < х²_кр , то нулевую гипотезу принимают.

Таким образом, алгоритм подбора теоретических распределений по статистическим данным следующий:

1. По статистическим данным строится полигон или гистограмма и рассчитываются соответствующие числовые характеристики.

2. По виду гистограммы выбирается линейное стандартное теоретическое распределение.

3. Для выражения теоретического закона рассчитывается теоретические вероятности p_i или теоретические частоты np_i.

4. По таблицам распределения Х² для выбранного α рассчитанного значения числа степени свободы выбирается х²_кр.

5. По выражению 6 рассчитывается Х²_набл

6. Если Х²_набл < х²_кр , гипотеза принимается, если Х²_набл > х²_кр , гипотеза отвергается.

Примечание:

Проверку соответствия эмпирического распределения выбранному теоретическому распределению можно выполнить по упрощенной схеме:

1. Вычисляем Х²_набл и обращаемся к таблицам Х² распределения. Пользуясь этими таблицами, можно для каждого значения Х² и числа степеней свободы r найти вероятность P того, что величина, распределённая по Х², превзойдёт его значение. (Х²_набл).

2. Распределение Х²даёт возможность оценить степень согласованности теоретического и статистического распределений. Будем исходить из того, что исследуемая случайная величина Х действительно распределена по выбранному теоретическому распределению. Тогда вероятность Р, определяется по таблице, есть вероятность того, что за счёт чисто случайных причин мера расхождения теоретического и статистического распределения будет не меньше, чем фактически наблюдаемое значение Х²_набл. Если эта вероятность мала, то нулевую гипотезу следует отвергнуть.

Напротив если Р сравнительно велика, можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счёт чисто случайных причин. Нулевую гипотезу можно считать правдоподобной или по крайней мере, не противоречащей. На практике, если Р окажется меньше 0,1, то гипотезу отвергают.

3. Синтез системы массового обслуживания типа М|M|M по заданным критериям качества.

Синтез системы М|M|M заданного качества выполняется на основании характеристик полученных в разделах I и II . По приведённым ниже математическим моделям введём следующие обозначения:

n – число сообщений, поступающих в СМО в единицу времени;

ω – число заявок, ожидающих обслуживания, единицы;

q – число заявок, находящихся в системе

t_а – временной интервал между поступающими сообщениями (время или период поступления);

t_s – время обслуживания заявки;

t_ω - время ожидания обслуживания;

t_q – время пребывания заявки в системе;

Е(n) – среднее число заявок, поступающих в систему в единицу времени;

Е(ω) – среднее число заявок, ожидающих обслуживания;

Е(q) – среднее число заявок, пребывающих в системе;

Е(ts) – среднее время обслуживания заявки;

Е(tω) – среднее время ожидания;

Р(n=N) – вероятность наличия N заявок в системе в данный момент времени;

{P(nN) – вероятность наличия N или более заявок в системе в данный момент времени;

E(t_a) – среднее время поступления;

E(t_a) =

P – коэффициент использования системы;

М – число приборов, работающих параллельно в системе со многими приборами;

P(q=N) – вероятность того, что в системе находится N заявок;

P(qN) – вероятность того, что q равно или больше N;

P(t_q>T) – вероятность того, что t_q больше заданного времени Т;

В – вероятность того, что в системе с многими приборами все приборы заняты при наличии очередей;

Р_в – вероятность того, что в системе со многими приборами все приборы заняты при отсутствии очередей (системы без очередей – заявки, обнаружив все приборы занятыми, покидают систему). Тогда коэффициент использования системы:

P =

Время пребывания в системе:

t_q = t_ω + t_s

Среднее время пребывания в системе:

E(t_q) = E(t_ω) + E(t_s)

Среднее число заявок ожидающих обслуживания:

E(ω) = E(n)E(t_ω)

Среднее число заявок в системе:

E(q) = E(n)E(t_q)

E(q) = E(ω) + PM

Вероятность того, что все приборы заняты при наличии очередей:

Среднее число заявок, ожидающих обслуживания:

E(ω) = B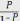

Среднее число заявок в системе:

Е(q) = B +MP

Среднее время ожидания обслуживания:

E(t_ω) =

Среднее время пребывания заявки в системе:

E (t_q) = +E(t_s)

Стандартное отклонение времени ожидания обслуживания:

δ t_ω = Стандартное отклонение времени пребывания в системе:

δ t_q = Вероятность того, что время ожиданияt_ω превысит заданное время T:

P (t_ω > T) = B e ^{–M(1-P)T/E(ts)}

Вероятность того ,что число заявок в системе равно или больше k:

P (q k) = , где

при N < M

при N M

Вероятность того, что все приборы заняты при очередей:

Внимание:

Если время обслуживания не является экспонентным, то

E (t_ω) =

E (ω) =