Лабораторная работа №1 Приближенное вычисление уравнения методом деления пополам (методом бисекций)

Пусть задана непрерывная функция и требуется найти корень уравнения . Предположим, что найден отрезок , такой, что. Тогда согласно теореме Больцано-Коши внутри отрезкасуществует точка, в которой значение функции равно нулю, т.е.,. Итерационный метод бисекций состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции(корень уравнения) с любой заданной точностью.

Опишем один шаг итераций. Пусть на -м шаге найден отрезок, такой, что. Делим его пополам точкойи вычисляем. Если, то корень уравнения. Если , то из двух половин отрезка выберем ту, на концах которой функция имеет противоположные знаки, так как один из корней лежит на этой половине. Таким образом,

, , если,

, , если.

Если требуется найти корень с точностью , то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше. Тогда координата середины отрезка и есть значение корня с требуемой точностью.

Метод бисекций – простой и надежный метод поиска простого корня^* уравнения . Он сходится для любых непрерывных функций, в том числе недифференцируемых. Скорость сходимости невелика. Для достижения точностинеобходимо совершитьитераций, где

.

Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.

Если на отрезке находится несколько корней уравнения, то процесс сходится к одному из них. Метод неприменим для отыскания кратных корней четного порядка. В случае кратных корней нечетного порядка он менее точен.

Лабораторная работа №2 Решение системы нелинейных уравнений методом Ньютона

Рассмотрим систему нелинейных уравнений снеизвестными

,

, (1)

……………….

или в векторной форме

, (1’)

где

, .

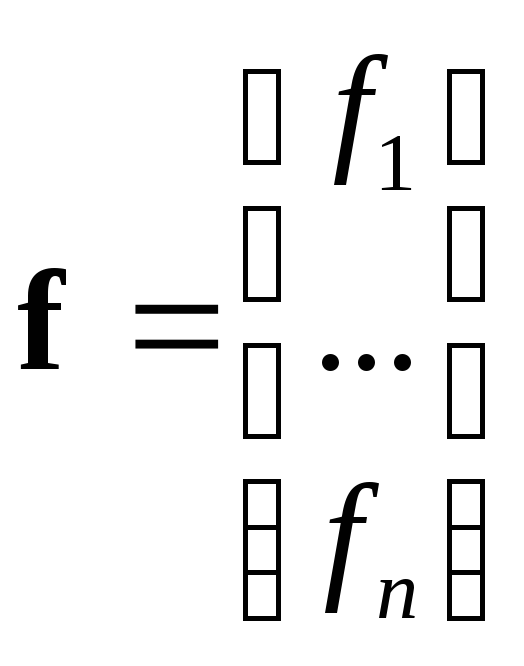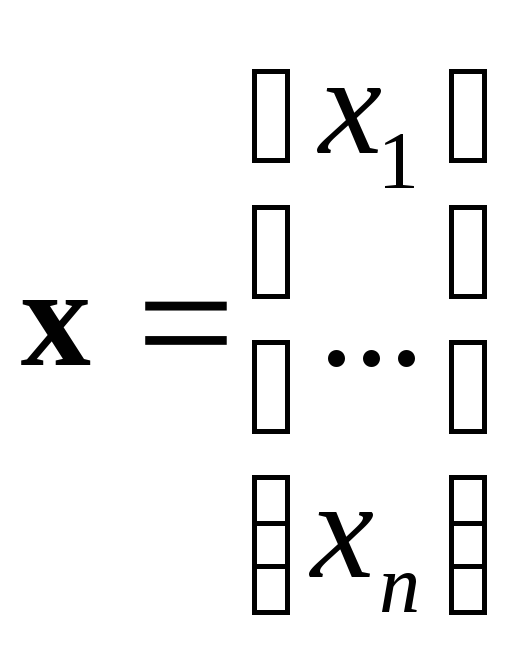Основная идея метода Ньютона состоит в выделении из уравнений системы линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем.

Пусть известно некоторое приближение корня. Тогда поправкуможно найти, решая систему

.

Для определения разложим векторную функциюв ряд по. Сохранив только линейные почасти, получим

.

Здесь через обозначена матрица производных.

Если , то, где– матрица, обратная матрице производных.

Таким образом, последовательные приближения корня можно вычислять по формуле

.

Отсюда видно, что метод Ньютона решения системы (1) состоит в построении итерационной последовательности:

. (2)

Если , то в достаточно малой окрестности корняитерационный процесс (2) сходится, причем с квадратичной скоростью, т.е. если, то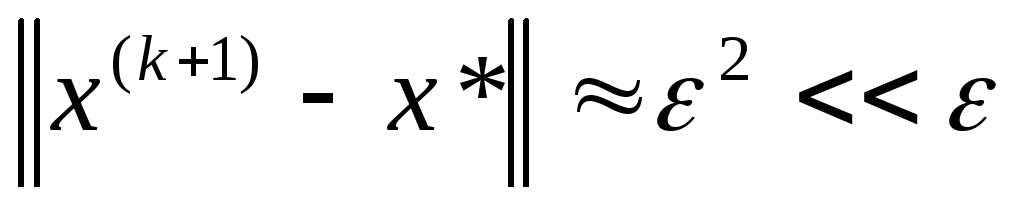. Поэтому в качестве критерия окончания итерационного процесса можно использовать условие. Если начальное приближение выбрано удачно, то метод Ньютона сходится очень быстро.

Лабораторная работа №3 Решение системы линейных уравнений методом Гаусса

Методом Гаусса называют точный^*) метод решения невырожденной системы линейных уравнений, состоящий в том, что последовательным исключением неизвестных систему

, ,

приводят к эквивалентной системе с треугольной матрицей

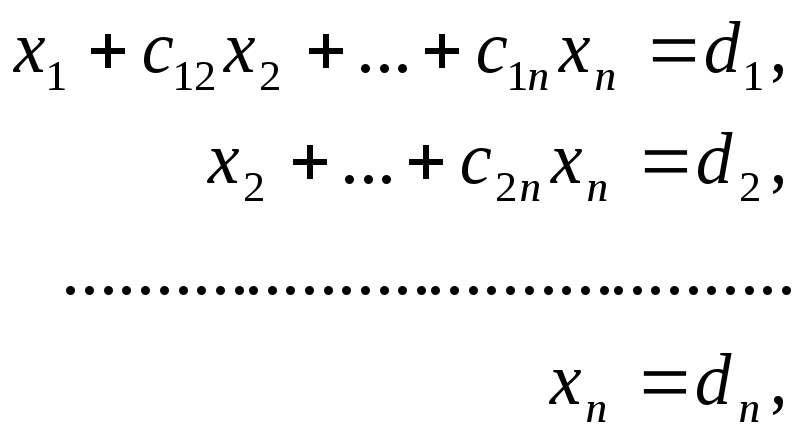
решение которой находят по рекуррентным формулам

, ,.

Существует много вариантов этого метода. Рассмотрим схему с выбором главного элемента. Пусть исходная система имеет вид

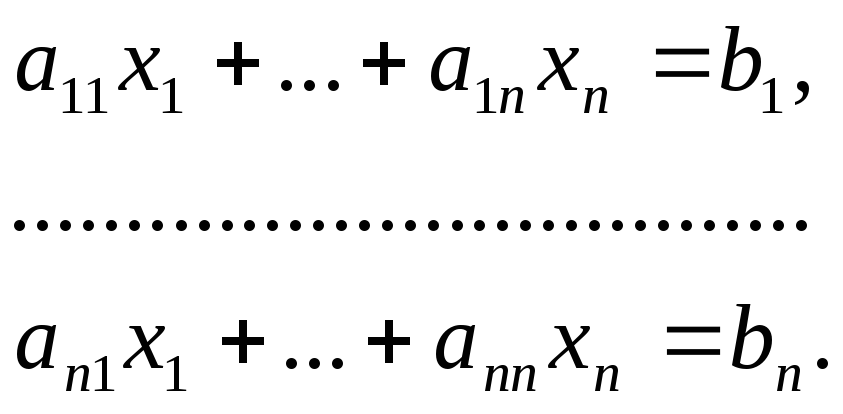(1)

Предположим, что , и разделим обе части первого уравнения системы на. В результате получим

, (2)

где ,,. С помощью уравнения (2) исключим во всех уравнениях системы (1), начиная со второго, слагаемые, содержащие. Для этого умножаем обе части уравнения (2) последовательно наи вычитаем соответственно из второго, третьего, …,n–го уравнения системы (1). В результате получаем систему, порядок которой на единицу меньше порядка исходной системы:

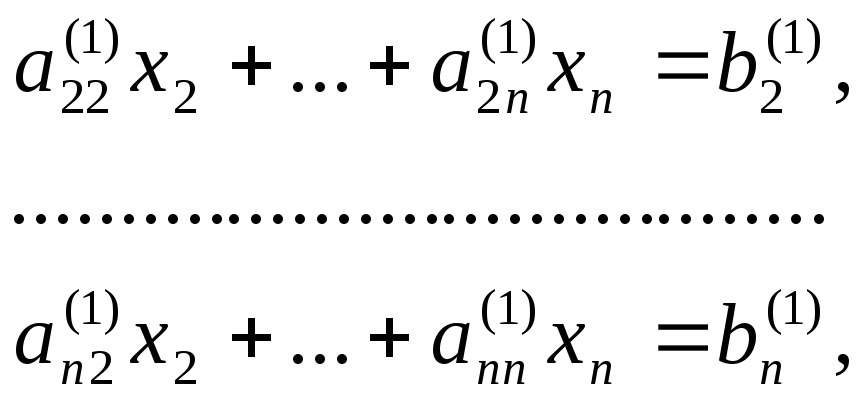
где ,,,.

Аналогично преобразуем полученную систему. В результате кратного повторения этого преобразования получим систему с треугольной матрицей

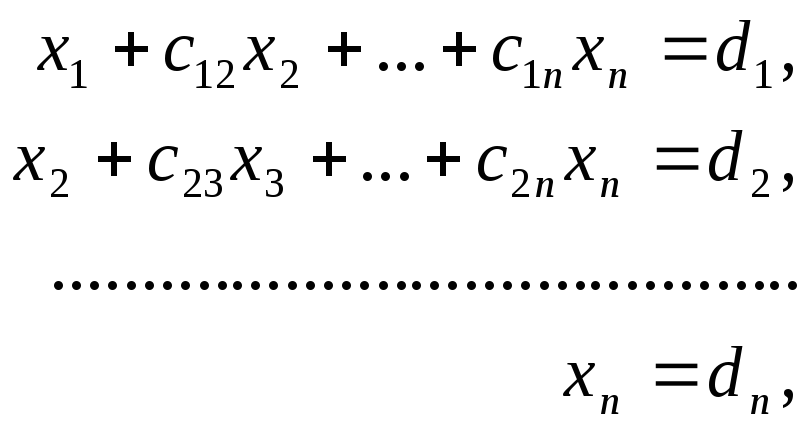(3)

которая эквивалентна системе (1) и легко решается. В самом деле, из последнего уравнения находим , подставляяв предпоследнее уравнение, найдем, затеми т.д. до, которое находим из первого уравнения системы, когда уже известны.

Таким образом, вычисления по методу Гаусса распадаются на два этапа: на первом этапе, называемом прямым ходом метода, исходную систему преобразуют к треугольному виду. На втором этапе, который называют обратным ходом, решают треугольную систему (3), эквивалентную исходной.

Коэффициенты называют ведущими элементами метода Гаусса. На каждом шаге предполагалось, что. Если окажется, что это не так, то в качестве ведущего элемента можно использовать любой другой ненулевой коэффициент системы. Однако если коэффициентмал, то после деления на этот элемент и вычитания-го уравнения из последующий возникают большие погрешности округления. Чтобы избежать этого, на каждом этапе уравнения переставляют так, чтобы на главной диагонали оказался наибольший по модулю элемент-го столбца. Если матрица системы хорошо обусловлена^*), то в методе Гаусса с выбором главного элемента погрешности округления невелики. Одновременно с решением системы можно найти определитель матрицы системы. Нетрудно убедиться, что определитель матрицы системы равен произведению ведущих элементов, т.е. .