Matematika / Модуль 2 / Лекция 5

Лекция 5.

Задача нелинейного программирования.

Метод множителей Лагранжа

Вопросы:

1. Постановка задачи и ее особенности

2. Функция Лагранжа

3. Метод множителей Лагранжа

4. Экономический смысл множителей Лагранжа

1. Постановка задачи и ее особенности

Задача математического программирования

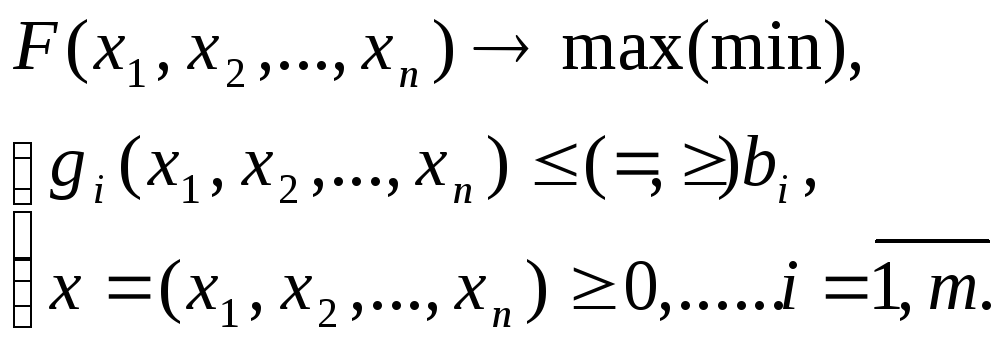
в которой либо целевая функция, либо ограничения, либо и то и другое нелинейны, называется задачей нелинейного программирования.

Нелинейные задачи составляют широкий класс настолько сложных задач, что до сих пор невозможно разработать общие методы, подобные симплекс-методу в линейном программировании, которые позволяли бы решить любые нелинейные задачи. Все возможные методы решения задач нелинейного программирования можно разделить на два больших класса: точные и приближенные методы решения. Точные методы позволяют определить решение для некоторых более узких задач, прежде всего задач с выпуклыми (вогнутыми) функциями F(x) и g_i(x). Приближенные (итерационные) методы позволяют решить практически любую задачу нелинейного программирования, однако, имеют свои недостатки: скорость сходимости (число шагов), точность и др.

Рассмотрим некоторые особенности задач нелинейного программирования на примере задач с двумя неизвестными. Так же, как и в линейном программировании, они допускают графическое решение.

Пример 1.

Решение

1. Построим допустимую область.

2. Построим линию уровня F(x) = Const.

Это окружность с центром в т. О₁(4; 6) и радиусом R = 2.

3. Увеличивая R (следовательно, и F), можно получить точки min F и max F. Это будут

т. А – т. минимума и т. В, т.С – точки локальных максимумов.

4. Координаты т. А находят из условия перпендикулярности (АО₁) и 2-й границы:

А(24/13; 36/13) F_min = 196/13.

B(1; 0) F_B = 45

C(6; 0) F_C = 40 т. В – точка максимума и F_max = 45.

Точка минимума не является вершиной допустимой области, а лежит на границе.

Пример 2. Та же допустимая область, а

Минимум F = 0 достигается в т. О₁(4; 1)

Точка минимума лежит внутри

допустимой области.

Минимум F = 25 достигается в т. А(0; 4)

Пример 3. .

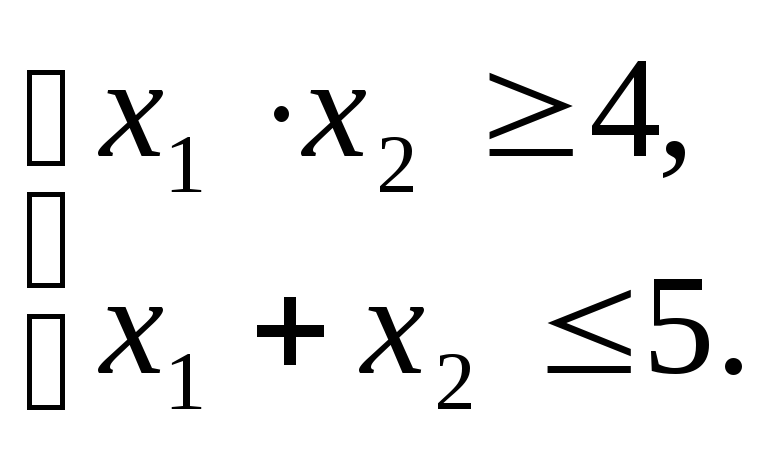
Решение

1. Допустимая область.

(1) гипербола х₂ = 4/х₁

(2)

2. Линия уровня F(x) = Const = 0

- парабола, …

3. т. А – т. max: А(4; 1), .

т. В – т. min – определяется приближенно , В(1,5; 2,67).

Точка минимума является точкой касания границы и линии уровня.

2. Функция Лагранжа

Пусть дана задача математического программирования

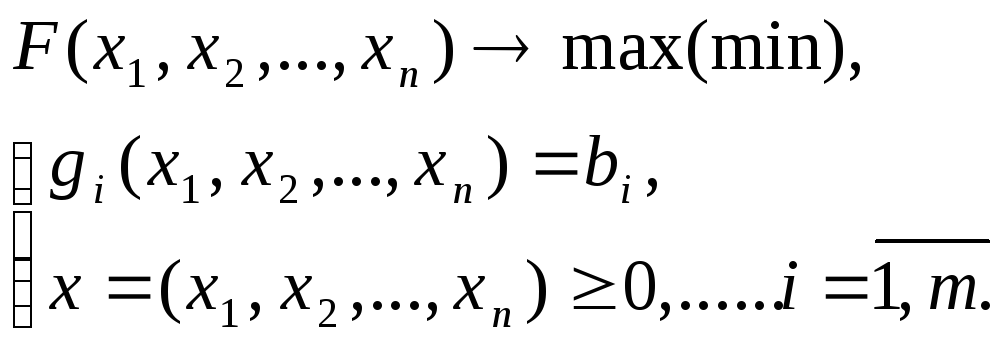
где функции F(x) и g(x) непрерывные вместе со своими частными производными. Эта задача является классической задачей на условный экстремум. Чтобы ее решить используют функцию Лагранжа.

Функцией Лагранжа называют функцию

,

где - множители Лагранжа.

Определим стационарные точки функции Лагранжа. Необходимые условия:

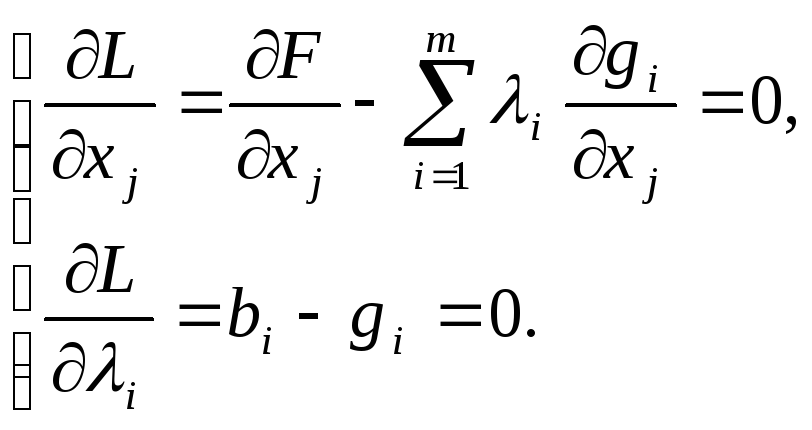
. (1)

Заметим, что вторая группа уравнений совпадает с ограничениями задачи. А если эти условия выполняются, то L(x, ) = F(x). Таким образом, решение системы (1) является не только стационарной точкой L(x,), но и стационарной точкой F(x), удовлетворяющей ограничениям задачи. Следовательно, решив систему (1), находят все точки, в которых целевая функция может иметь экстремум.

Существуют и достаточные условия, определяющие точки максимума или минимума или отсутствие экстремума. Эти условия определяются знаком второго дифференциала.

3. Метод множителей Лагранжа

1. Составить функцию Лагранжа.

2. Найти и приравнять нулю.

3. Решая систему (1), находят точки, в которых F(x) может иметь экстремум.

4. Среди точек, подозрительных на экстремум, находят такие, в которых

достигается экстремум, и вычисляют значения F(x) в этих точках.

5. Определяют точки максимума и минимума.

Пример. На двух предприятиях отрасли необходимо изготовить 200 изделий некоторой продукции. Затраты, связанные с производством х₁ изделий на первом предприятии, равны 4х₁² руб., а затраты, обусловленные изготовлением х₂ изделий на втором предприятии, составляют 20х₂ + 6х₂² руб. Определить, сколько изделий на каждом из предприятий следует произвести, чтобы общие затраты, обусловленные изготовлением необходимой продукции, были минимальны.

Решение

1. Составим математическую модель.

.

2. Составим функцию Лагранжа

3. ; ; .

4. , , .

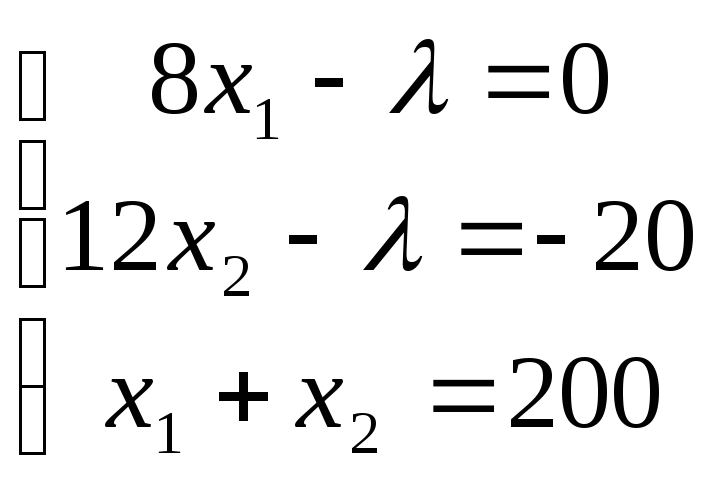
Замечание. Метод множителей Лагранжа можно применять и в случае, когда ограничения заданы в виде неравенств. При этом следует сначала найти точки безусловного экстремума и среди них выбрать те, которые удовлетворяют ограничениям задачи, затем определить точки, удовлетворяющие системе (1).

4. Экономический смысл множителей Лагранжа

Пусть дана задача

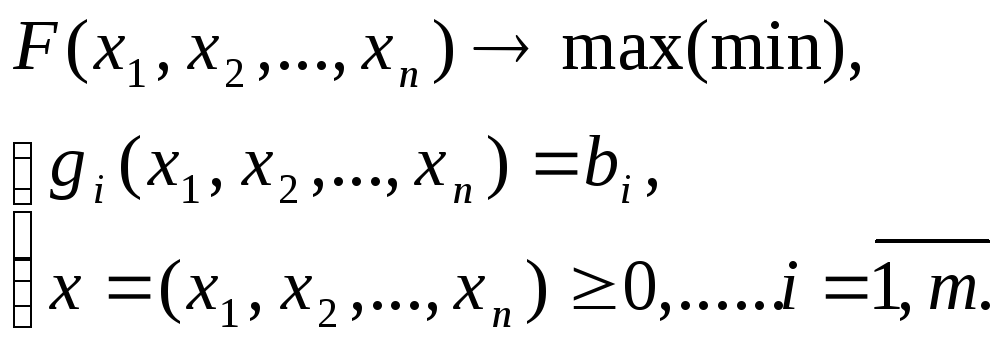
Точка экстремума х*, F(x*) = F*. Если значения b_i могут изменяться, то х* зависит от b_i: х*_j = x_j(b) и

(2)

С другой стороны, из ограничений следует

(3)

(Если k-е ограничение дифференцируется по b_i, то = 0)

Кроме того, в точке экстремума выполняются условия (1). Откуда

.

Подставив это выражение и (3) в (2), получим

.

Если интерпретировать F доход или стоимость, b_i – как затраты некоторых ресурсов, то множители Лагранжа будут показывать, как изменится максимальный доход (или минимальная стоимость), если количество ресурса i-го вида увеличится на единицу.