4. Задача коммивояжера

Пусть имеется граф и заданы длины его дуг. Требуется среди всех контуров (контуром называют путь, который начинается и заканчивается в одной и той же вершине), проходящих точно по одному разу через каждую из вершин графа, найти контур наименьшей длины. Контуры такого вида называют маршрутами. Свое название задача получила от одной из возможных конкретизаций: коммивояжер (бродячий торговец) должен объехать nгородов, побывав в каждом из них по одному разу, и вернуться в исходный город. Ясно, что здесь разумно использовать маршрут кратчайшей длины. Условия задачи обычно задаются в виде так называемой матрицы расстояний, то есть таблицы следующего вида

J I	1	2	…	n
1	a11	a12	…	a1n
2	a21	a22	…	a2n
…	…	…	…	…
n	an1	an2	…	ann

Здесь i,j– номера вершин графа,a_ij– длина дугиx_ix_j, выходящей из вершиныx_iи входящей в вершинуx_j. Если дугиx_ix_jв графе нет, то вместо числаa_ijставится «-». Длины дугx_ix_j иx_jx_iмогут быть различными, то есть не обязательноa_ij=a_ji.

Задача коммивояжера является задачей дискретного программирования. Решение задачи коммивояжера рассмотрим на конкретном примере.

Схема решения:

1. Начальный шаг – применяется однократно.

Определяется нижняя граница множества всех маршрутов, заданных матрицей . Нижняя граница вычисляется с помощью операции приведения, основанной на следующем факте: при уменьшении всех чисел какой-либо строки (столбца) на одно и то же число, длины всех маршрутов уменьшаются на это же число, так как в длину каждого маршрута входит в качестве слагаемого только по одному числу из каждой строки (столбца) матрицы. Кратчайший маршрут при этом остается прежним, но его длина уменьшается на указанное число.

Операция приведения:

1. приведение по строкам: определяется minчисло в каждой строке, записывается справа в каждой строке;

2. это число вычитается из всех элементов этой строки;

3. приведение по столбцам: определяется minчисло в каждом столбце, записывается внизу в каждом столбце;

4. это число вычитается из всех элементов этого столбца;

5. новая приведенная матрица обозначается .

Каждая строка и каждый столбец приведенной матрицы содержит хотя бы один нулевой элемент. Числа, которые вычитались, называются постоянными приведения. Так как каждая постоянная приведения входит как слагаемое в длину любого маршрута, то длина любого маршрута не меньше суммы всех постоянных приведения. Следовательно, за нижнюю границу на множествеможно принять сумму всех постоянных приведения. Этим способом вычисляют нижнюю границуи в дальнейшем.

Замечание. Если для любого маршрута вычислить его длинуLпо матрицеи его длинуL⁰матрице, то они связаны соотношениемL=L⁰+.

2. Общий шаг – повторяется многократно.

Операция ветвления:

Выбирается некоторая дуга , и все множестворазбивается на два непересекающихся подмножества: и. Исключение дуги эквивалентно замене соответствующего ей расстояния в матрице прочерком «-».

1. дуга для ветвления выбирается так, чтобы нижняя граница множества 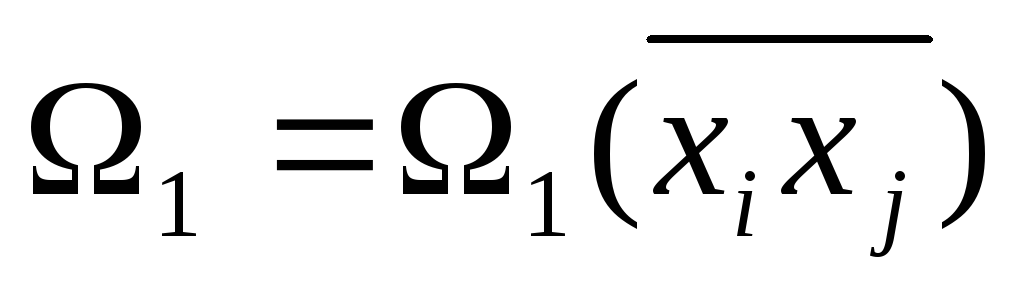была, по возможности, большей, то есть, чтобы при исключении этой дуги была большей сумма возникающих при этом постоянных приведения. Ясно, что положительные постоянные при ведения появятся лишь в случае, когда после исключения дуги в одном из соответствующих ей рядов (строк или столбцов) матрицы расстояний нет нулевых элементов. Поэтому в исходной приведенной матрице ей должен соответствовать нулевой элемент, а в соответствующих ей строке и столбце (хотя бы в одном из них) не должно быть, по возможности, нулевых элементов.

Описанный способ выбора дуги основывается на следующих соображениях: а) большее значение нижней границы для позволяет надеяться, что в дальнейшем это множество будет отсечено; б) включение дуги нулевой длины во все маршрутыделает их в какой-то степени «более перспективными». Поэтому в первую очередь рассматривают множество.

2. Все маршруты матрицы содержат выбранную дугу, которой отвечает клетка, расположенная на пересеченииi-той строки иj-того столбца матрицы. Следовательно, дуги, отвечающие остальным клеткамi-той строки иj-того столбца, не войдут ни в один из маршрутов, а тогда эти ряды необходимо удалить из матрицы. Кроме того, так как все маршруты матрицысодержат дугу, то они не могут содержать дуги. В противном случае получился бы контур, который не содержит всех вершин. 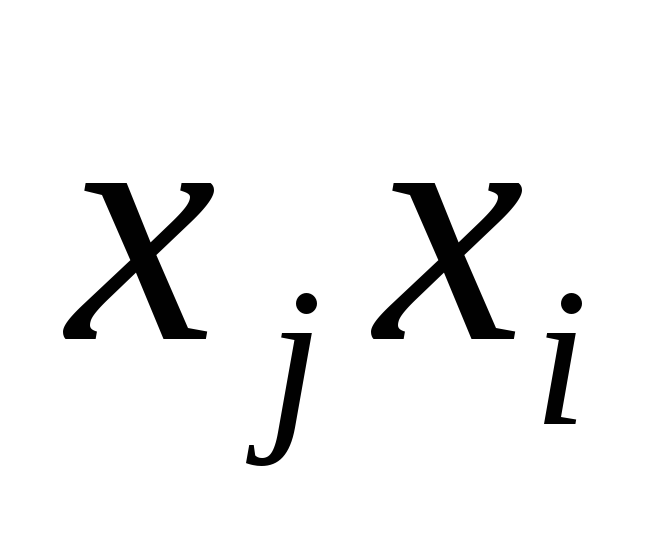Поэтому дугавдолжна быть исключена.

Окончательно следует: а) исключить из матрицы строкуiи столбецj; б) заменить противоположную дугупрочерком «-».

Замечания.

1. При повторном применении операции ветвления для образования множества маршрутов, содержащих дугу , необходимо следить за тем, чтобы из ранее включенных в маршрут дуг и этой дуги не могли образоваться замкнутые контуры, не содержащие всех пунктов.

2. Операция ветвления повторяется до тех пор, пока не будет получен замкнутый маршрут.

3. Проверка оптимальности решения.

Для этого сравнивают длину полученного замкнутого маршрута с нижними границами концевых множеств. При этом отсекаются все концевые множества, имеющие нижнюю границу, большую чем найденная.

Замечание.После операции отсечения могут возникнуть два случая: 1) все концевые множества оказались отсеченными. Это означает, что найденный маршрут является искомым, то есть имеет наименьшую длину; 2) есть концевые множества, нижние границы которых меньше длины найденного маршрута. В этом случае выбирается неотсеченное множество с наименьшей нижней границей и к нему применяется общий шаг. После каждого применения общего шага следует сравнивать нижние границы вновь полученных множеств.