2. Правила построения двойственной задачи.

Исходя из общего вида прямой и двойственной задач можно установить связь между этими задачами, позволяющую для любой ЗЛП строить двойственную ей задачу.

Свойства двойственных задач (правила).

1. Число неизвестных двойственной задачи равно числу ограничений прямой задачи. Число ограничений двойственной задачи равно числу неизвестных прямой задачи.

2. Матрица коэффициентов двойственной задачи является транспонированной матрицей коэффициентов прямой задачи.

3. Коэффициенты целевой функции двойственной задачи являются свободными членами ограничений прямой задачи.

4. Свободные члены ограничений двойственной задачи являются коэффициентами целевой функции прямой задачи.

5. Если ограничения прямой задачи записаны со знаком меньше или равно (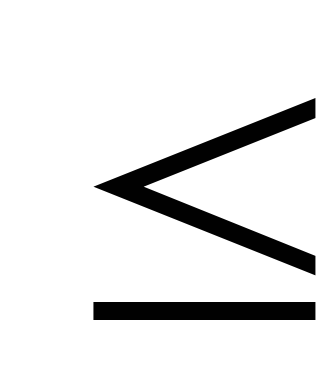), то ограничения двойственной задачи записываются со знаком больше или равно ( ).

6. Если ограничение прямой задачи задано в виде уравнения, то соответствующее неизвестное двойственной задачи не ограничено знаком.

7. Если какое-либо неизвестное прямой задачи не ограничено знаком, то соответствующее ограничение двойственной задачи будет задано в виде равенства.

8. Если целевая функция прямой задачи сформулирована на максимум, то целевая функция двойственной задачи будет сформулирована на минимум.

Существует много различных комбинаций ограничений и целевой функции для записи исходной задачи. Для упрощения задачи построения двойственной задачи запишем прямую задачу в некотором стандартном виде прямой задачи. Этот вид предполагает, что:

1. все ограничения имеют знак ;

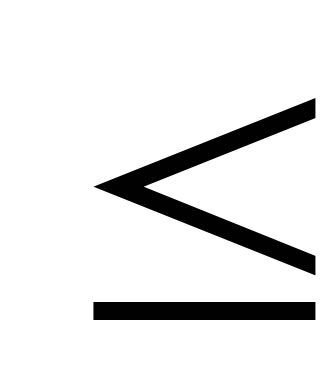2. целевая функция сформулирована на максимум;

3. все неизвестные неотрицательны.

Чтобы записать прямую задачу в стандартном виде, необходимо:

1. неравенство со знаком умножить на (-1);

2. равенство заменить на два неравенства противоположных знаков, одно из которых следует умножить на (-1);

3. формулировку целевой функции меняют заменой знаков коэффициентов на противоположные;

4. если переменное x_j не ограничено знаком, его можно представить в виде разности двух неотрицательных переменных.

Пример. Составить двойственную задачу к исходной.

.

Решение. 1) Стандартный вид прямой задачи.

2) Двойственная задача:

Задачу можно записать в виде, соответствующем исходной прямой задаче, если заменить:

а) - не ограничена знаком,

б) два последних ограничения соответствуют равенству.

.

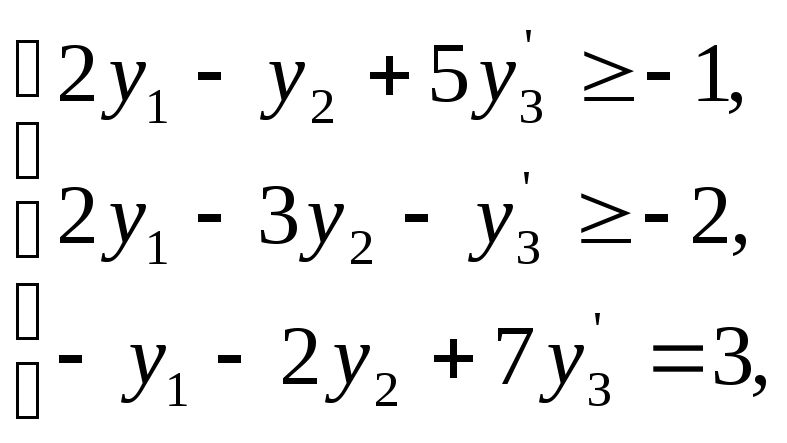
3. Основные теоремы двойственности и их экономическое содержание.

Теорема 1. Двойственная задача к двойственной есть прямая задача.

Доказательство:

Пусть имеем пару двойственных задач в матричном виде.

Ах А^Тy C

F = C^Tx Z =

x 0 y 0

Построим к двойственной задаче двойственную:

1) запишем в стандартном виде -А^Тy -C

Z = -

2) -Ах Ах

F = - C^Tx F = C^Tx

Что и требовалось доказать.

Теорема 2. Значение функции F, соответствующее любому допустимо-

му решению прямой задачи, не больше значения функции Z,

соответствующего любому допустимому решению

двойственной задачи.

Доказательство: Пусть X и Y соответственно произвольные допустимые решения прямой и двойственной задач. Следовательно,

1) Ах и Y Y^Т , Y^TAX Y^Tb = b^TY = Z.

2) A^TY C и X 0 X^Т , X^TA^TY X^TC = C^TX = F.

3) выражение X^TA^TY – скалярная величина (число) она равна

своей транспозиции, т.е. X^TA^TY = Y^TAX. Итак, имеем,

F X^TA^TY = Y^TAX Z F Z.

Что и требовалось доказать.

Следствия: 1) если в прямой задаче допустимая область не пуста, а целевая функция не ограничена сверху, то у двойственной задачи допустимая область пуста;

2) если в двойственной задаче допустимая область не пуста, а целевая функция не ограничена снизу, то у прямой задачи допустимая область пуста.

Теорема 3. Если прямая задача имеет конечное оптимальное решение F = F_max, то двойственная задача имеет конечное оптимальное решение Z = Z_min. При этом F_max = Z_min, а симплекс-множители оптимального решения прямой задачи являются значениями переменных в оптимальном решении двойственной задачи.

Доказательство:

Запишем прямую задачу Ах , x 0 , b , F = C^Tx .

Запишем задачу в стандартном виде Ах + х^Р = b, где

х^Р = (х₁,…,х_n+m)- дополнительные, уравновешивающие переменные, ^Т- симплекс-множители оптимального решения. Известно, что прямая задача разрешима, следовательно, можно определить значения симплекс-множителей оптимального решения. Получим оптимальное выражение целевой функции, то есть

+

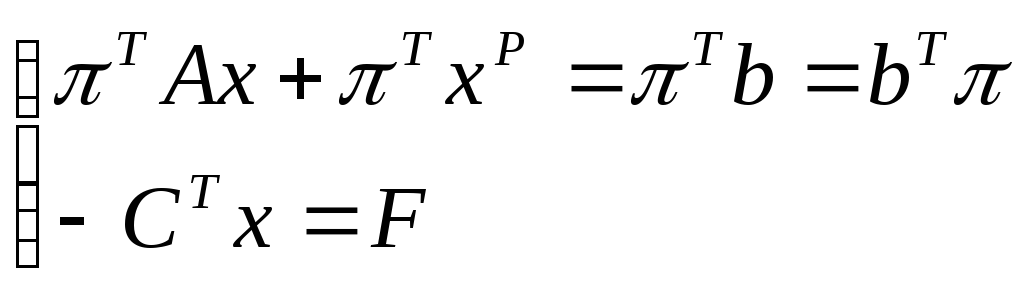
(-С^T+)x+= F + b^T. (*)

Так как это оптимальный вид целевой функции, то все коэффициенты неотрицательны.

или .

Т.о., если y = , то ограничения двойственной задачи выполняются.

Так как (*) – оптимальный вид целевой функции, то коэффициенты перед базисными переменными равны нулю, а свободные переменные сами равны нулю F_min = -b^T или F_max = b^T. Если y = , то это и есть целевая функция двойственной задачи, то есть Z = F_max = Z_min. Что и требовалось доказать.

Теорема 4. Если двойственная задача имеет конечное оптимальное решение Z = Z_min, то прямая задача имеет конечное оптимальное решение F = F_max. При этом Z_min = F_max , а значения симплекс-множителей оптимального решения двойственной задачи являются значениями переменных в оптимальном решении прямой задачи с противоположными знаками (если обе задачи решаются прямым симплекс-методом).

Доказательство: В матричной форме двойственная задача имеет вид.

А^Тy C , y 0, С 0, Z =

1) Запишем в стандартном виде A^Ty – y^S = C, где y^S= (y_m+1,…,y_m+n)^T 0 – дополнительные, уравновешивающие переменные, - симплекс-множители оптимального решения двойственной задачи. Для двойственной задачи имеют то же значение, то есть

+

(b^T + = Z + . (**)

Так как это оптимальный вид целевой функции Z, то все коэффициенты неотрицательны.

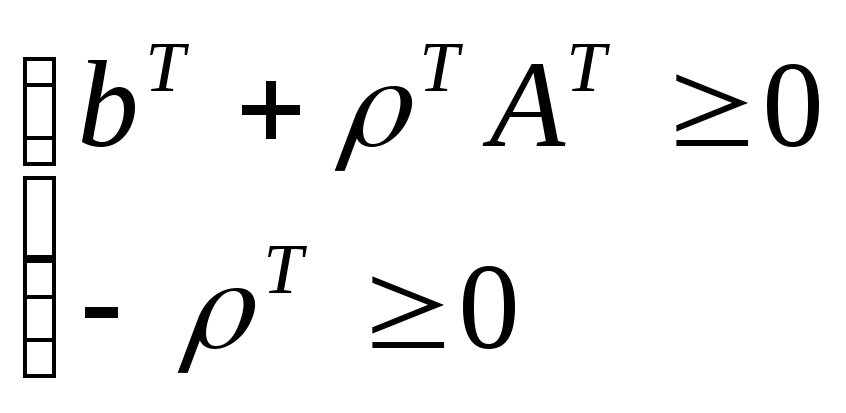или .

Таким образом, если , то ограничения прямой задачи

удовлетворяются, значит, это решение.

2) Так как (**) – оптимальное решение для целевой функции, то коэффициенты перед базисными переменными равны нулю, а свободные переменные сами равны нулю. Следовательно,

Z_min = -, а это есть целевая функция прямой задачи, если . Что и требовалось доказать.

Экономическое содержание теорем состоит в следующем: если задача оптимизации плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. План производства и оценки ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Так как F Z, Z – F = - издержки производства, которые равны нулю когда F^* = Z^*.

Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенство общей оценки продукции и ресурсов, и обуславливают убыточность всякого другого плана, отличного от оптимального. Кроме того, если y_i > 0, то при оптимальной производственной программе этот ресурс используется полностью; если y_i = 0, то ресурс используется не полностью.