Литература / Конспект лекций по МО ЦОС (факультет ВМиК МГУ) / LSSDIG23 / LSSDIG23

2

Лекция 23. Метод главных компонентов в задаче сжатия

Идея сжатия сигнала на основе разложения по ортогональному базису была изложена выше. Рассмотренные базисы являются универсальными и не учитывают особенность сигнала. Когда имеется набор сигналов одной природы, возникает вопрос о выборе оптимального базиса, пригодного для сжатия всего семейства. Эта задача решается с помощью метода главных компонентов. Сначала нам понадобится вспомогательное утверждение из линейной алгебры.

Предложение 1. Пусть имеется вещественная симметрическая матрица и натуральное , меньше чем размер матрицы. Среди матриц вида , где - ортогональная матрица, выбирается такая, в которой сумма первых диагональный элементов максимальна. Тогда эта сумма совпадает с суммой наибольших корней .

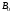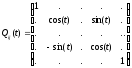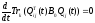Доказательство. Очевидно, что максимум достигается на некоторой матрице . Положим - элементарный поворот, затрагивающий строки и столбцы с номерами . Обозначим через сумму первых диагональных элементов матрицы . По определению при . Очевидно, что при . В этих обозначениях производная в нуле принимает вид . Взяв индексы , получим, что . Это означает, что искомая матрица 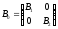. Поскольку набор корней матриц исчерпывает множество корней , отсюда следует утверждение.

Постановка задачи

Перейдем к постановке задачи о выборе оптимального базиса. Имеются векторов . Требуется найти систему из ортонормированных векторов таких, что выполнено условие

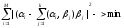(1)

Его содержательный смысл - сумма квадратов отклонений от проекций на плоскость, порожденную векторами минимальна. Перепишем (1) в виде

. Поскольку первое слагаемое от векторов не зависит, последнее заменяется условием , (2)

где . Условие (2) сводится к ситуации, описанной Предложением 1. В частности, в качестве векторов можно выбирать собственные векторы, отвечающие наибольшим собственным значениям матрицы . Следует отметить, что любой ортонормированный базис в пространстве, порожденном этими собственными векторами, обладает нужными свойствами.

Отметим, что сумма квадратов отклонений совпадает с суммой оставшихся собственных значений матрицы , которая в нашем случае является неотрицательно определенной.