- •Теплофизические параметры газов
- •Основные уравнения газодинамики
- •Газодинамические функции потока
- •Общее условие перехода от дозвукового течения к сверхзвуковому и обратно
- •Геометрическое сопло (сопло Лаваля)
- •Расходное сопло
- •Механическое сопло
- •Тепловое сопло
- •3. Косые скачки уплотнения
- •3.3 Определение параметров потока в косом скачке
- •3.4 Кинематические соотношения для косого скачка
- •3.5 Волновое сопротивление косого скачка
3. Косые скачки уплотнения
3.1 Образование косого скачка уплотнения
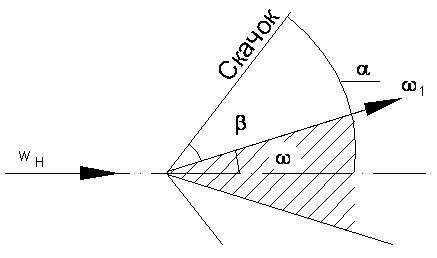
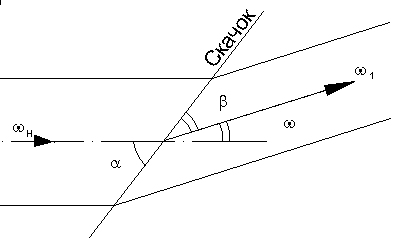
В косом скачке уплотнения фронт ударной волны располагается наклонно к направлению потока. Возникает он тогда, когда пересекая фронт скачка газовый поток должен изменить направление, например, при сверхзвуковом обтекании газом клиновидного тела.
 =
=
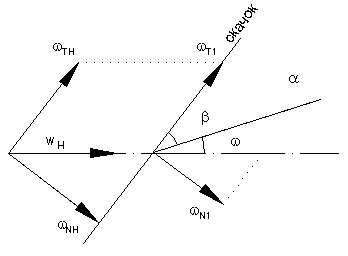
Разложим векторы скорости до скачка Н и после скачка 1 на составляющие параллельно фронту и нормально фронту ударной волны (скачка). При этом тангенциальная составляющая остаётся постоянной t=const, а нормальная составляющая уменьшается NH > N1.
.2 Температуры частичного торможения
В косом скачке уравнение теплосодержания для теплоизолированного потока
![]() .
.
Из треугольника скоростей
![]() ,
но
,
но
![]() .
.
Откуда
![]() .
.
Выведем понятие температуры частичного торможения, понимая под ним температуру, которую будет иметь поток не при полном торможении, а лишь при погашении нормальных к фронту скачка составляющих скорости
![]()
3.3 Определение параметров потока в косом скачке
Если учесть уравнение состояния в виде
![]() ,
,
то можно показать, что косой скачек уплотнения описывается такими же уравнениями, что и прямой скачек, с той лишь разницей, что в первом случае вместо полной скорости присутствуют нормальные к фронту скачка компоненты, а вместо температуры полного торможения Т0 - температура частичного торможения Т.
![]() ,
,
![]() ,
,
здесь
![]() -
частичная критическая сокость, которая
соответсвует температуре частичного
торможения Т.
-
частичная критическая сокость, которая
соответсвует температуре частичного
торможения Т.
3.4 Кинематические соотношения для косого скачка
![]() ,
,
а связь между полной и частичной критическими скоростями определяется уравнением:
![]() ,
т.к.
,
т.к.
![]() и
и
![]() .
.
Переходя к коэффициентам скорости
![]() ;
;
![]() или
или![]() .
.
3.5 Волновое сопротивление косого скачка
Изменение полного и статического давлений в косом скачке определяется соответсвенными для прямого скачка уравнениями, если вместо H вставить величину NH:
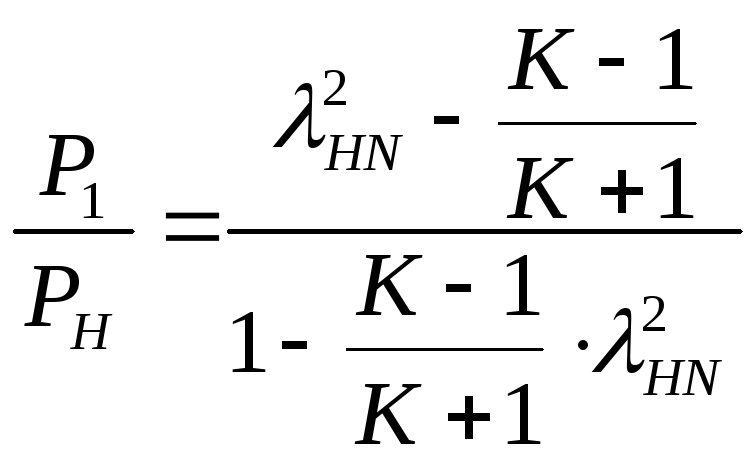
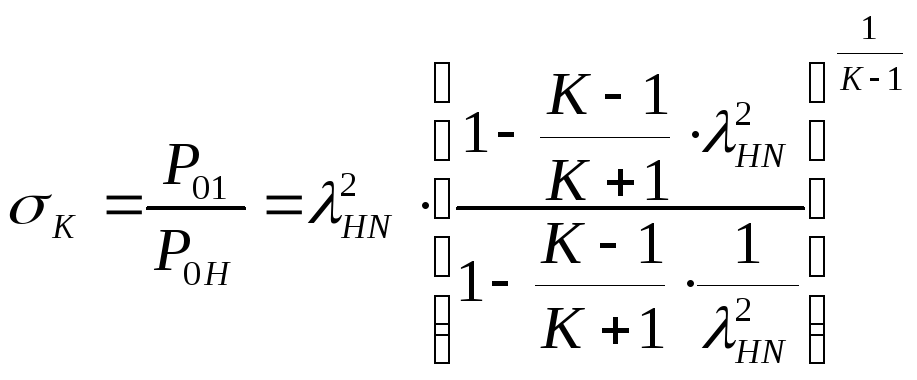
3.5 Интенсивность косого скачка. Угол отклонения потока в косом скачке.
Если связать эти изменения с абсолютной скоростью набегающего потока, то получим следующие уравнения.
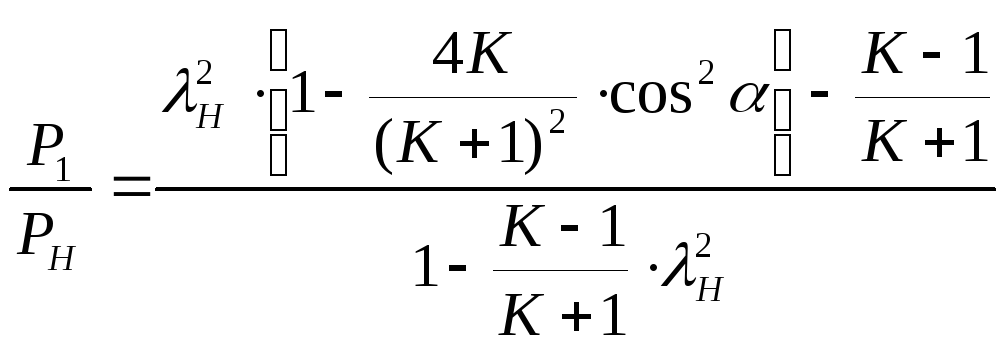
![]() ,
где
,
где
![]()
![]()
где
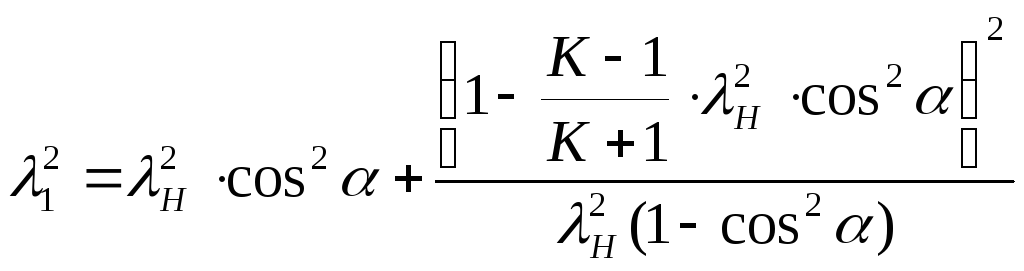
Если вывести эти зависимости в функции от числа М:
![]()
откуда видно, что при одной и той же скорости набегающего потока (MH=const) косой скачек всегда бывает слабее прямого и интенсивность его изменяется с изменением угла наклона фронта скачка к направлению набегающего потока.
Уравнение, связывающее отношение с числом М и углом наклона скачка
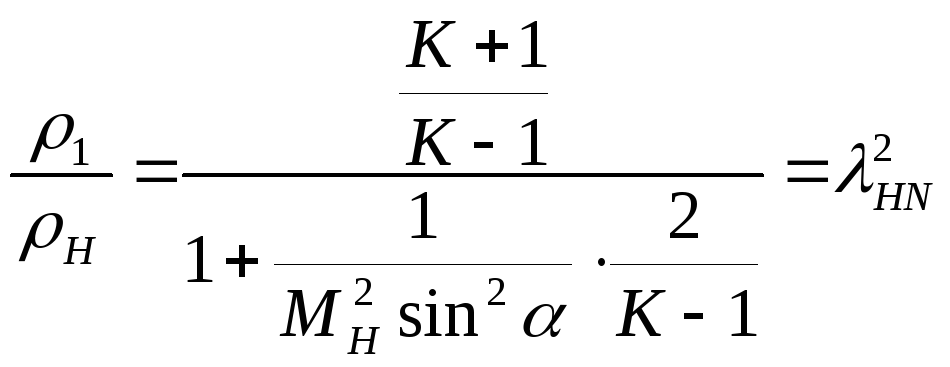
Зная соотношение плоскостей, можно вычислить угол ω, на который отклоняется поток в скачке:
![]()
с учетом уравнения неразрывности
![]()
![]() или
или