5. Геометрическое сопло (сопло Лаваля)

Отсутствуют все прочие воздействия, кроме геометрического . Уравнение газового потока имеет вид:

Для ускорения дозвукового потока необходимо сужение канала и при достижения критической скорости (M=1) необходимо расширение канала .

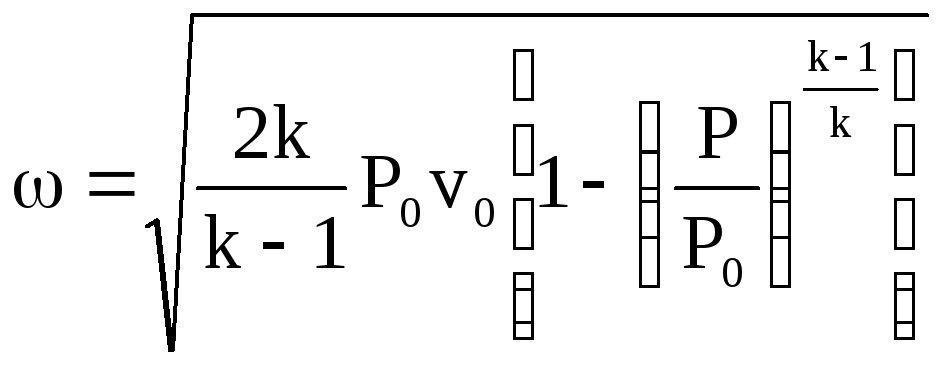
Параметры:

;

;

Связь между скоростью потока и сечением сопла устанавливается уравнением неразрывности:

Учитывая, что и:

После подстановки:

Из формулы видно, что безразмерное значение площади является функцией только числа Маха. Эта функция имеет вид:

Если задается конфигурация сопла, то можно указать, какое число Маха получится в любом сечении. Для одного и того же значения имеется два значения числа Маха: одно в дозвуковой, другое в сверхзвуковой области. А так как параметры потока однозначно зависят от числа Маха, то выбрав определенное произвольное сечение сопла () получим определенное значение числа Маха, которому соответствуют определенные значения температуры, давления, плотности:

;

;

.

Во многих случаях расчетные формулы упрощаются, если параметры состояния газа определяются в функции не от числа Маха, а от коэффициента скорости :

6. Расходное сопло

В расходном сопле переход через скорость звука осуществляется за счёт изменения расхода газа в трубе постоянного сечения (dF=0) при отсутствии теплообмена с окружающей средой (), без совершения внешней работы () и без трения ().

Уравнение потока принимает вид:

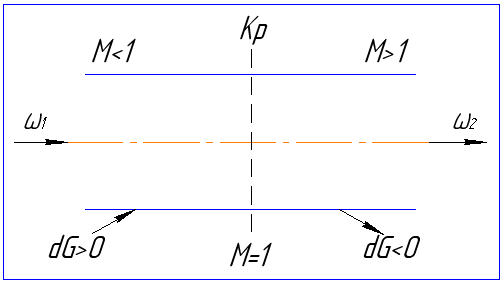
Ускорение газового потока в дозвуковой части канала достигается путём подвода дополнительной массы газа (dG0) и отвода газа (dG0) в сверхзвуковой части канала.

7. Механическое сопло

В механическом сопле перевод потока из дозвукового в сверхзвуковой осуществляется за счёт изменения технической работы () при отсутствии других воздействий (т.е.dF=0, dG=0, ,).

Уравнение потока принимает вид:

Если газ совершает работу (), например на колесе турбины, то в дозвуковом режиме (М он ускоряется(d, а в сверхзвуковом (М замедляется (d. Непрерывный переход через скорость звука можно обеспечить, если после критического сечения к газу подвести энергию, например в нагнетателе. Таким образом сверхзвуковое механическое сопло должно состоять из последовательно расположенных турбины (в области М) и компрессора (в области М) между которыми располагается критическое сечение.

8. Тепловое сопло

Переход газового потока через скорость звука осуществляется за счет теплового воздействия при отсутствии всех прочих (dF=0, , , dG=0, dQ≠0).

Уравнение движения потока принимает вид:

Из уравнения следует, что ускорение газового потока (d в дозвуковой части (М) можно обеспечить подводом теплоты (dQ0), а в сверхзвуковой – отводом теплоты (dQ0).

Скачки уплотнения

1. Механизм образования скачков.

При движении тела с большой скоростью впереди него образуется пространство с повышенным давлением среды, которое вызывает сопротивление движению тела.

Повышенное давление в этой области газовой среды распространяется с большой скоростью во все стороны в виде волн давления. Основная особенность волн давления заключается в том, что фронт волн очень узок, и поэтому состояние газа изменяется скачком. В связи с этим ударные волны называются скачками уплотнения.

Рассмотрим механизм образования скачков.

Под влиянием резкого смешения поршня в трубе перед поршнем возникает и распространяется волна сжатия. За бесконечно малый промежуток времени d фронт волны переместится на расстояние dx. При этом в области H-1 за время d произошло повышение давления от P_н (давление невозмущенного потока) до P₁ (давление за фронтом волны). В соответствии с повышением давления произошло и повышение плотности на величину

Повышение плотности означает, что из объема 0-H в объем перетечет элементарное количество газа:

Из уравнения неразрывности можно определить скорость газового потока за фронтом волны:

или

но производная dx/d - это скорость распространения волны _В; тогда

Из уравнения количества движения

; _Н=0

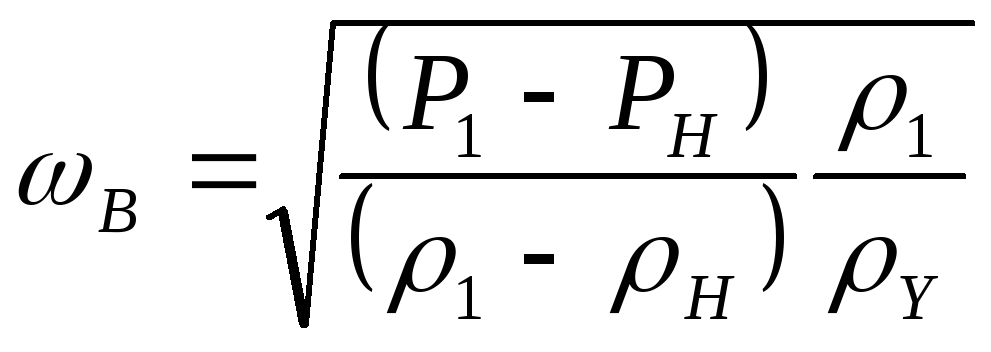
тогда скорость потока за фронтом волны

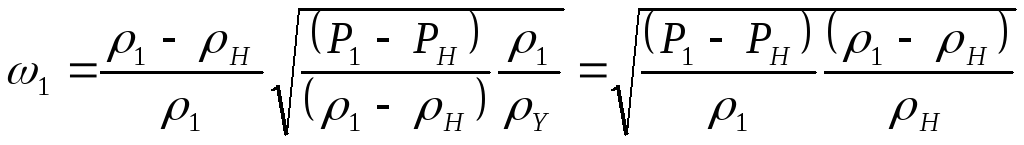
2. Прямой скачок уплотнения. Параметры потока в скачке.

Если фронт ударной волны составляет прямой угол с направлением движения потока, то такая волна называется прямой ударной волной или прямым скачком уплотнения. Такой скачек называется косым скачком уплотнения.

1. Из уравнения неразрывности

2. Из уравнения количества движения

с учётом (1) имеем

т.е.

Для энергетически изолированного потока, когда dQ=0 и l₀=const из

для температуры потока перед скачком имеем

из уравнения состояния газа

и , тогда

, но ,

или

аналогично

.

Вычтем P₁-P_H,

.

Из уравнения количества движения

,

тогда

или

.

Принимая во внимание, что

запишем

.

Отношение изменения давления к изменению плотности в скачке пропорционально этому отношению до скачка.

3. Основное кинематическое соотношение.

Критическая скорость

,

но

, тогда

.

Для скачка имеем

, тогда

,

.

В прямом скачке уплотнения всегда сверхзвуковая скорость газового потока переходит в дозвуковую. При этом чем больше значение коэффициента скорости перед скачком (_Н), тем меньше его значение после скачка (₁), т.е. чем выше начальная скорость газа (_Н), тем сильнее получается скачок уплотнения.

4. Уравнение ударной адиабаты.

Используя

,

, получим

.

Значение скобки

,

тогда

.

, но , а

, тогда

, или

.

Запишем так

.

Левую часть разделим на _Н, правую часть на Р₁:

;

При неограниченном возрастании давления в скачке (Р) увеличение плотности в скачке имеет предел

, для воздуха