
- •Теплофизические параметры газов
- •Основные уравнения газодинамики
- •Газодинамические функции потока
- •Общее условие перехода от дозвукового течения к сверхзвуковому и обратно
- •Геометрическое сопло (сопло Лаваля)
- •Расходное сопло
- •Механическое сопло
- •Тепловое сопло
- •3. Косые скачки уплотнения
- •3.3 Определение параметров потока в косом скачке
- •3.4 Кинематические соотношения для косого скачка
- •3.5 Волновое сопротивление косого скачка
Теплофизические параметры газов
Температура:
![]() (Реомюра);
(Реомюра);
![]()
![]()
![]()
Давление, Р:
![]() –нормальная
атмосфера;
–нормальная
атмосфера;
![]() –техническая
атмосфера;
–техническая
атмосфера;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Плотность:
![]()
Сжимаемость – свойство газа изменять свой объем при изменении давления. Характеризуется коэффициентом сжимаемости: отношение изменения объема газа
 при
изменении давления
при
изменении давления на
на к первоначальному объему газаV.
к первоначальному объему газаV.
![]()
Величина
обратная
![]() – модуль упругости Е:
– модуль упругости Е:
![]()
Изменение объема газа в зависимости от изменения температуры характеризуется коэффициентом температурного расширения:
![]()
Вязкость – свойство газа оказывать сопротивление относительному сдвигу частиц. Ньютон установил что сила сдвига
 пропорциональна вязкости, плотности
и градиенту скорости:
пропорциональна вязкости, плотности
и градиенту скорости:
![]() ,
,
где:
![]() – коэффициент кинематической вязкости,
– коэффициент кинематической вязкости,![]() (
(![]() (Стока);
(Стока);
![]() –коэффициент
динамической вязкости,
–коэффициент
динамической вязкости,
![]() .
.
Теплоемкость:

![]()
![]() ,
,
где: К – показатель адиабаты;
R – газовая постоянная.
![]() ;
;
![]() .
.
Основные уравнения газодинамики
Уравнение состояния для идеального газа (Уравнение Менделеева - Клайперона):
![]()
![]()
Уравнение Ван-дер-Ваальса для реального газа:
![]()
Значения коэффициентов «а» и «в» можно найти в литературе
Мягков М.П. «Справочник по физико-техническим основам глубокого охлаждения».
|
|
a,
|
b,
|
|
Аммиак |
|
|
|
Кислород |
|
|
|
Воздух |
|
|
|
Фреон 12 |
|
|
Уравнение неразрывности
Рассмотрим стационарное течение элементарной струи газа, поперечные размеры которой настолько малы ,что в каждом ее сечении постоянными являются все основные параметры потока: скорость, давление, температура и плотность. Выделим участок струйки между сечениями 1 и 2. За бесконечно малый промежуток времени d эта часть струйки переместится в положение 1-2. Перемещение струйки можно рассматривать как перемещение газа из объёма 1-1 в объём 2-2.
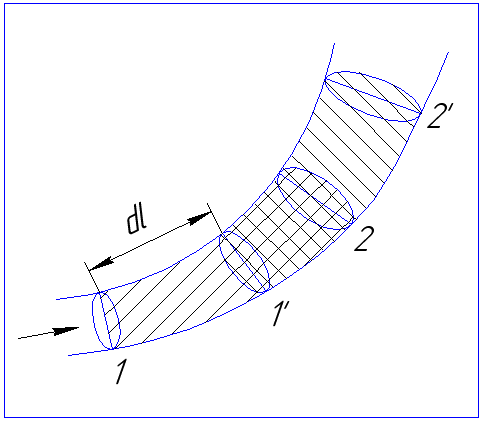
Количество газа, перетекающего из объёма 1-1 ,составляет:
![]() (кг),
(кг),
где
![]() .
.
Тогда
![]() , кг.
, кг.
Приток газа в объём 2-2 составляет:
![]() ,
(кг).
,
(кг).
В соответствии с законом сохранения массы:
![]() ,
или
,
или
![]() и
из этого следует, что:
и
из этого следует, что:
![]()
Уравнение неразрывности потока газа.
Для
несжимаемой жидкости, когда
![]() :
:
![]()
В дифференциальной форме уравнение неразрывности:
![]() имеет
вид:
имеет
вид:
![]()
или
поделив на
![]() имеем:
имеем:
![]()
Уравнение количества движения.
В
соответствии с законом Ньютона
элементарное изменение количества
движения
![]() равно элементарному импульсу силы
равно элементарному импульсу силы![]() :
:
![]() ,
,
где: P – сумма проекций всех сил на ось;
-проекция скорости на ту же ось;
d – время действия силы P.
В гидродинамической форме уравнение количества движения выведено Эйлером и применительно к элементарной струйке потока газа имеем:
![]()
![]()
![]()
Рассмотрим
изменение суммарного количества движения
![]() за время
за время![]() .
Изменение суммарного количества движения
элементарной струйки можно рассматривать
как изменение количеств движения для
масс 1-1
и 2-2,
так как масса 1-2
остается общей для обоих положений
струйки.
.
Изменение суммарного количества движения
элементарной струйки можно рассматривать
как изменение количеств движения для
масс 1-1
и 2-2,
так как масса 1-2
остается общей для обоих положений
струйки.

Прирост суммарного количества движения равен разности количеств движения масс 2-2 и 1-1.
![]() ,
,
где:
![]() – масса газа в элементе 1-1
или 2-2,
кг;
– масса газа в элементе 1-1
или 2-2,
кг;
![]() и
и
![]() – проекции скоростей в сечениях 1 и 2 на
осьx.
– проекции скоростей в сечениях 1 и 2 на
осьx.
![]() ,
,
где G – секундный весовой расход газа, кг/с.
Тогда:
![]()
Откуда:
![]() ,
или
,
или
![]() -
уравнение Эйлера
-
уравнение Эйлера
Аналогичные уравнения можно составить для других осей.
Рассмотрим элементарную струйку , расположенную параллельно оси х.

![]()
![]()
Проекция
силы, действия машины на газ –
![]() .
Тогда сумма проекций всех сил на ось х
равна:
.
Тогда сумма проекций всех сил на ось х
равна:
![]()
Тогда уравнение Эйлера имеет вид:
![]()
Если расстояние между сечениями 1 и 2 бесконечно мало (dl), то уравнение количества движения записывается в дифференциальной форме:
![]()
![]()
Используя
уравнение неразрывности
![]() и разделив все наF
имеем:
и разделив все наF
имеем:
![]() ,
или
,
или
![]()
Если отсутствуют силы трения и силовое воздействие на газ имеем:
![]() ,
или
,
или
![]()
Это уравнение выражает важное свойство газового потока: при отсутствии сил трения и внешних сил увеличение скорости потока (d>) может быть вызвано только уменьшением статистического давления (dP<0) и наоборот, торможение потока всегда связано с увеличением давления в нем.
В интегральной форме уравнение количества движения:
![]()
Если
![]() и
и![]() ,
то:
,
то:
![]() ,
или
,
или
![]()
Из уравнения неразрывности:
![]() .
.
И
для цилиндрической струйки когда
![]() :
:
![]() ,
и тогда:
,
и тогда:
![]() ,
откуда:
,
откуда:
![]()
В цилиндрической струйке давление может измениться в случае изменения скорости, что может быть достигнуто подводом или отводом теплоты.
Уравнение энергии.
Составим баланс энергии для элементарной струйки при перетекании из объёма 1-2 в объём 1'-2' за бесконечно малый промежуток d. Так как объём 1'-2 является общим, то приращение энергии измеряется разностью количеств энергии в бесконечно малых объемах 2 - 2 и 1-1.

Приращения кинетической энергии
![]()
Приращение потенциальной энергии:
![]()
Приращение внутренней энергии:
![]()
Используя,
что
![]() ,
а
,
а![]() можно записать:
можно записать:
![]()
Работа сил давления:
![]()
![]()
![]()
На
участке 1-2 за время d
может быть подведена теплота dQ
и струйка может совершать техническую
работу
![]() и на преодоление сил трения
и на преодоление сил трения![]() .
.
Согласно первому закону термодинамики подведённая к газу тепловая энергия и работа сил давления расходуются на совершение технической работы, работы сил трения, а также на повышение запасов потенциальной, внутренней и кинетической энергии.

Или для единицы веса газа:
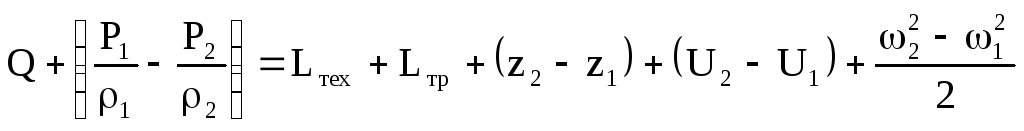
Уравнение Бернулли.
Уравнение энергии для 1кг газа:
![]()
В дифференциальной форме:
![]() (1)
(1)
В соответствие с первым законом термодинамики тепло, подведённое к газу, может расходоваться только на повышение внутренней энергии и работы расширения (деформации):
![]() (2)
(2)
Вычитая из (1) уравнения (2) получим:
![]() ,
или:
,
или:
![]() –уравнение
Бернулли в дифференциальной форме, так
как
–уравнение
Бернулли в дифференциальной форме, так
как
![]()
После интегрирования:
![]() –обобщенное
уравнение Бернулли.
–обобщенное
уравнение Бернулли.
Сила
изохорического процесса при v=const
(![]() ):
):
![]()
В изобарическом процессе (Р=const):
![]()
В изотермическом процессе при P=RT:
![]()
В
адиабатическом процессе при
![]() :
:

При
отсутствии технической работы и
гидравлических потерь
![]() и
и![]() ,
а запас потенциальной энергии не
изменяется
,
а запас потенциальной энергии не
изменяется![]() ,
уравнение имеет вид:
,
уравнение имеет вид:
![]()
В случае, когда =const (для идеальной несжимаемой жидкости):
![]() ,
и уравнение приобретет вид:
,
и уравнение приобретет вид:
![]() ,
или:
,
или:
![]() ,
или:
,
или:
![]() –полное
давление потока.
–полное
давление потока.
Величина
![]() – скоростной напор или динамическое
давление потока.
– скоростной напор или динамическое
давление потока.
