12.6. Характеристики заторможенного потока. Газодинамические функции

Параметры газа, соответствующие нулевой скорости потока, называются параметрами торможения. Давление, плотность, температура и энтальпия, соответствующие этому состоянию называются давлением, плотностью, температурой и энтальпией торможения и обозначаются p_o, r_o, T_o, i_o. Соотношение между местными параметрами потока и параметрами торможения определяются с помощью газодинамических функций t, p, e.

Аргументом газодинамических функций является число Маха

или коэффициент скорости . ГдеV - местная скорость потока, а - скорость звука в газе, - критическая скорость звука. Установим связь между числом Маха и коэффициентом скорости. Запишем уравнение энергии в виде

.

Разделим уравнение на , получим

.

Отсюда

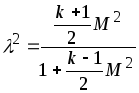
или разрешив относительно числа Маха, имеем

.

Для вывода газодинамических функций запишем уравнение энергии

.

Умножим уравнение на и учтем, что. В результате имеем

.

Уравнение состояния газа , записанное для параметров торможения, позволяет получить соотношение

.

Из уравнения адиабаты по аналогии для параметров торможения имеем

.

Из последних трех равенств имеем

, .

Воспользуемся теперь выражением для газодинамической функции t, запишем

,

.

Газодинамические функции широко используются для расчета изэнтропических течений газа. Во многих учебниках по газовой динамике они представлены в виде таблиц. Из выражений для газодинамических функций при М = l = 1 критические параметры газа могут быть найдены через параметры торможения p_o, r_o, T_o

, ,.

При практических расчетах используют еще одну газодинамическую функцию, называемую удельным секундным расходом q :

.

Воспользовавшись выражением для газодинамической функции e а также связью между критическими параметрами и параметрами торможению, учитывая , имеем

.

Нетрудно заметить, что при l = 0 и получимq=0. В первом случае расход равен нулю, так как газ неподвижен. Во втором случае p = r = T = 0.

12.7. Волна разрежения

Слабые возмущения в газе распространяются со скоростью звука, влияние слабого изменения давления, вызываемого помещенным в равномерный сверхзвуковой поток источником возмущений ( например, телом ) не может распространятся вверх по потоку, а сносится вниз по потоку со скоростью большей скорости звука, оставаясь внутри так называемого конуса возмущений.

Рис. 59

При установившемся сверхзвуковом течении вдоль стенки с изломом ( рис. 59 ) возмущения, идущие от всех точек линий излома, ограничены огибающей конусов возмущений - плоскостью, наклоненной к направлению потока под углом m, таким, что .

Далее за этой плоскостью поток поворачивается, расширяясь внутри угловой области, образованной пучком плоских фронтов возмущений ( характеристик ), до тех пор, пока не станет параллельным направлению стенки после излома. Если стенка между двумя прямолинейными участками искривляется непрерывно, то поворот потока происходит постепенно в последовательности прямых характеристик, исходящих из каждой точки искривленного участка стенки. Параметры газа постоянны вдоль прямых характеристик. Такие течения называются течениями Прадтля-Майера ( рис. 60, 61 ). Рассматриваемое течение имеет свойства конических, так как физические величины на любом из лучей не зависят от расстояния до центра разворота.

Рис. 60

Рис. 61

Будем считать течение потенциальным. Скорость в произвольной точке D в пределах сектора разворота удобно разложить на компоненты V_s и V_r , направленные вдоль луча и по нормали к нему. При этом V_s нормальная к линии возмущения компонента скорости всегда звуковая V_s = a . Параметры газа на линиях возмущения не зависят от угла e ( e отсчитывается от нормали к передней линии угла разворота, поэтому потенциал течения в секторе АОВ можно представить в виде :

.

Найдем компоненты скорости

,

.

Решение задачи обтекания выпуклого угла состоит в нахождении зависимости газодинамических характеристик потока от их значений в набегающем потоке и угла поворота потока q .

Рассмотрим в начале случай М = 1. Воспользуемся уравнением энергии

,

где 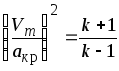. Учитывая, что, получим

.

С учетом связи компонент скорости, имеем

.

Разделяя переменные, получим

.

Здесь . Проинтегрируем предыдущее уравнение

.

Так как приe=0, то с=0.

.

Найдем зависимость . Представимчерез компоненты скорости :

.

Откуда получаем

Из рис. 61 видно, что

.

Так как , то. Приравнивая соотношения дляe, получим искомую зависимость :

. (*)

Рис. 62

Обращенная зависимость может быть получена только для некоторых значенийk. Чтобы обобщить полученное соотношение на случай когда М1 > 1, вводят понятие фиктивного угла qф . qф - это тот угол, на который следует повернуть звуковой поток, чтобы получить М1 > 1 ( рис. 62 ). Угол qф находят по формуле (*), подставляя туда М=М1 .

Затем определяют суммарный угол поворота :

.

Пользуясь той же формулой, по известному q_с определяют М₂. Из выражения (*) следует, что по мере увеличения q число Маха растет. Можно получить предельный угол поворота звукового потока, при котором он ускоряется до М=¥ . Подставляя М=¥ в (*), имеем

.

При k = 1.4 q_m= 129^o30`.

На практике такой разворот реализовать невозможно. В результате действия сил вязкости при определенных значениях q наступает отрыв потока.