Выводы из графиков Никурадзе

• При ламинарном течении шероховатость практически не влияет на сопротивление. Эксперимент практически полностью подтверждает с теоретические формулы.

• Критическое число Рейнольдса от шероховатости не зависит (штриховые кривые отклоняются от прямой A в одной точке).

• В области турбулентных течений при небольших числах Рейнольдса и малой шероховатости сопротивление от шероховатости не зависит (штриховая линия совпадает с прямой B), а с увеличением Re сопротивление возрастает.

• При больших значениях чисел Рейнольдса перестаёт зависеть отRe и становится постоянным для определённой относительной шероховатости.

Местные гидравлические сопротивления

Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения. В этих местах интенсивно теряется напор. Примерами местных сопротивлений могут быть искривления оси трубопровода, изменения проходных сечений любых гидравлических аппаратов, стыки трубопроводов и т.п. Потери напора на местных сопротивлениях определяются по формуле Вейсбаха:

;

где -коэффициент местного сопротивления.

Коэффициент местного сопротивления зависит от конкретных геометрических размеров местного сопротивления и его формы. В связи со сложностью процессов, которые происходят при движении жидкости через местные сопротивления, в большинстве случаев его приходится определять на основании экспериментальных данных.

Однако в некоторых случаях величины коэффициентов местных сопротивлений можно определить аналитически.

Из определения коэффициента видно, что он учитывает все виды потерь энергии потока жидкости на участке местного сопротивления. Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления.

Коэффициенты различных сопротивлений можно найти в гидравлических справочниках. В том случае, если местные сопротивления находятся на расстоянии меньше (25÷50)d друг от друга (- диаметр трубопровода, соединяющего местные сопротивления), весьма вероятно их взаимное влияние друг на друга, а их действительные коэффициенты местных сопротивлений будут отличаться от табличных. Такие сопротивления нужно рассматривать как единое сложное сопротивление, коэффициенткоторого определяется только экспериментально. Нужно отметить, что из-за взаимного влияния местных сопротивлений, расположенных вблизи друг друга в потоке, во многих случаях суммарная потеря напора не равна простой сумме потерь напора на каждом из этих сопротивлений.

Виды местных сопротивлений Внезапное расширение.

В этом случае, одном из немногих, выражение для потери напора можно найти теоретическим путем.

При внезапном расширении потока в трубке от сечения1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот. На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Тогда появляется вопрос, о каких потерях идёт речь? Дело в том, что показания пьезометра зависят не только от потерь энергии, но и от величины давления. А давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае надо учитывать, что если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше.

Назвав разность потерянной скоростью, можно сказать, чтопотеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.

Последнюю формулу можно переписать в виде:

или .

С учетом того, что на основании уравнения неразрывности потока , те же потери напора можно представить в виде:

или .

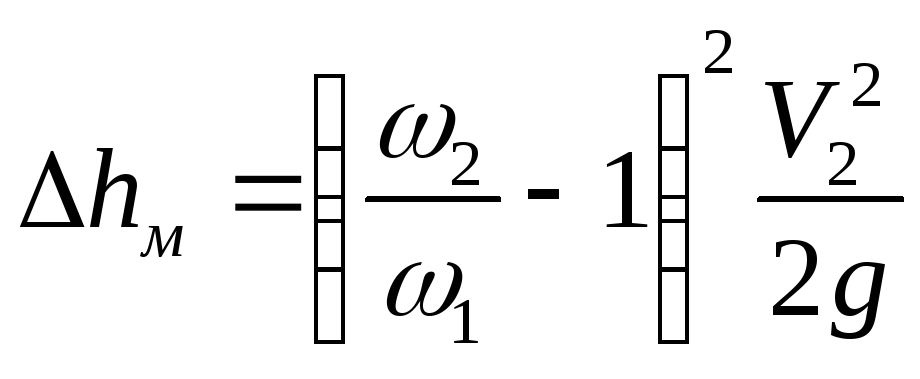Сравнивая последние выражения с формулой Вейсбаха , можно выделить выражения длякоэффициента местного сопротивления при внезапном расширении потока:

, если определять по скорости;

, если определять по скорости.