Гидравлические потери по длине

Потери напора по длине, иначе их называют потерями напора на трение , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью

,

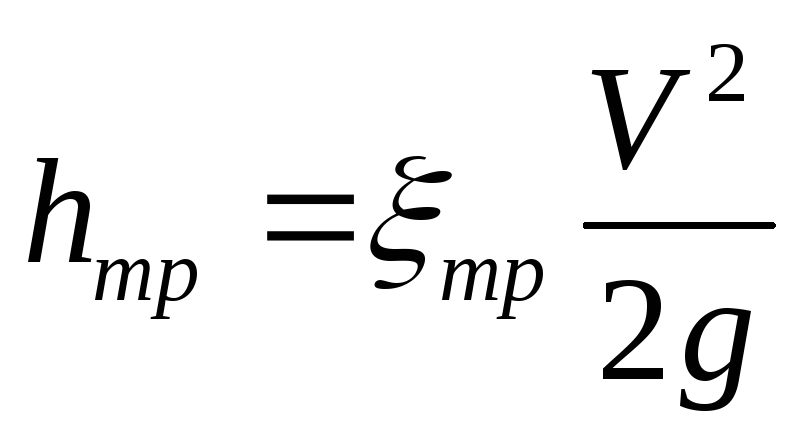где - коэффициент сопротивления, обусловленный трением по длине.

При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы

,

где – коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).

Из этого выражения нетрудно видеть, что значение  - коэффициент трения участка круглой трубы, длина которого равна её диаметру.

С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси

.

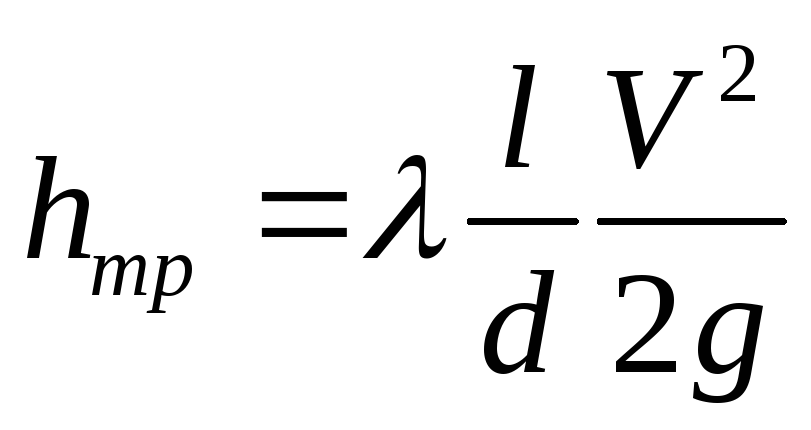Эту формулу можно применять не только для цилиндрических трубопроводов, но тогда надо выразить диаметр трубопровода d через гидравлический радиус потока

или

где, напомним, ω – площадь живого сечения потока,

χ - смоченный периметр.

Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид

.

Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине λ не является величиной постоянной.

Для определения физического смысла коэффициентаλ рассмотрим объём жидкости длиной l, который равномерно движется в трубе диаметром d со скоростью V. На этот объём действуют силы давления P₁ и P₂, причём P₁ > P₂, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы τ₀. Условием равномерного движения под действием сказанных сил будет следующее равенство:

.

Если учесть, что

, ^то ,

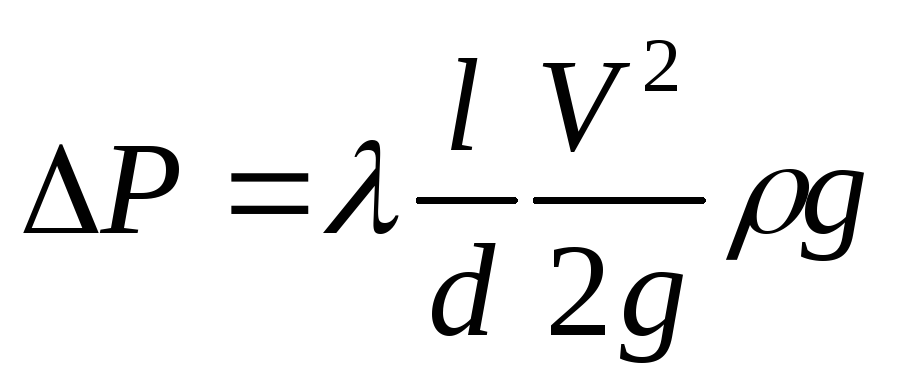и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:

.

Сократив последнее выражение, получим . Выразив из негоλ, окончательно будем иметь

.

Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков. Однако коэффициент λ не является величиной постоянной и зависит от многих факторов. Для выяснения его величины, и связанных с ним потерь энергии необходимо подробно проанализировать режимы движения жидкости.

Ламинарное течение жидкости

Используя значение скорости u, определим величину расхода через кольцевую площадь dω_c шириной dr, находящуюся на расстоянии r от центра трубы. Выше было отмечено, что скорость в любой точке этого кольца одинакова, и тогда

.

Проинтегрировав dQ по всей площади трубы (т.е. от r = 0 до r = r₀), получим

Средняя скорость в таком потоке будет

Заметим, что средняя скорость потока с параболическим распределением скоростей вдвое меньше максимальной.

Из последнего выражения легко получить закон сопротивления потоку, т.е. зависимость потерь энергии от размеров и параметров движения жидкости:

Заменив в этом выражении динамический коэффициент вязкостикинематическим и выразив радиус трубыr₀ через диаметр d, получим

Полученное выражение носит название закона Пуазейля и применяется для расчета потерь энергии с ламинарным течением.

Эту же величину потерь на трение ранее мы выразили формулой Дарси. Если приравнять правые части формулы Дарси и закона Пуазейля, получится:

Заменим расход произведением и подставим в последнее равенство

.

Искусственно умножим и разделим числитель и знаменатель на V:

Очевидно, что в этом случае

.

Это выражение для коэффициента гидравлического трения при ламинарном движении жидкости хорошо подтверждается экспериментом и используется на практике для определения потерь энергии в потоке при ламинарном течении. Иногда этот коэффициент обозначается .