6. Статические и динамические характеристики пневматическо­го привода

6.1. Исполнительные устройства

Пневматические исполнительные механизмы - устройства, преобразующие энергию сжатого газа в энергию перемещения вы­ходного механического звена привода. В пневматических робото-технических устройствах в подавляющем большинстве использу­ют поршневые исполнительные механизмы в силу простоты их конструкции, надежности и обеспечения значительного рабочего усилия.

Поршневой привод конструктивно может быть выполнен в виде привода одностороннего действия или двухстороннего дей­ствия.

Подача воздуха в рабочие полости цилиндра выполняется с помощью распределителя. В качестве распределителя использу­ются конструкции в виде цилиндрического золотника, плоского золотника, струйной трубки.

Усилие трогания поршня из положения покоя определяется зависимостью

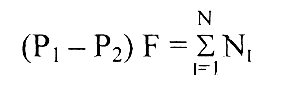
Р₁ - давление в полости нагнетания,

Р₂ - давление в полости опорожнения,

F - площадь поршня,

- сумма сил, действующих на поршень.

Для определения уравнений динамики газа в полостях при­вода принимаются следующие допущения:

• проходные сечения цилиндра выполнены в виде дросселей с турбулентным режимом течения;

• процесс наполнения и опорожнения газа происходит в ади­абатическом режиме;

- режим течения через дроссели - квазистационарный. Масса газа в рабочей полости цилиндра М =(6.1)

Дифференцируя данную зависимость по времени и использую уравнения для идеального газа Р =, получим

(6.2)

Данное изменение массы представляет, собой массовый рас­ход газа G. Величина расхода G определяется по известным зави­симостям для докритического и надкритического режимов истече­ния для воздуха. После подстановки зависимостей в выражение (6.2) и интегрирования можно получить следующие зависимости для времени заполнения рабочей камеры:

- для режима докритического истечения:

Под конечным значением P_КОН понимается давление, при котором начинается движение поршня.

V₀ - начальный объем подпоршневой полости,

P_НАЧ - начальное давление в рабочей полости, обычно

P_НАЧ =P_АТ

Характер изменения давления в рабочей полости в период наполнения до начала движения определяется зависимостью (6.2), где расход G должен соответствовать режиму истечения.

При движении поршня во время рабочего цикла объем рабо­чей полости меняется от V_МIN до V_МAX при прямом ходе, от V_МAX до V_МIN при обратном ходе.

Рассмотрим уравнение состояния воздуха в рабочей полости при прямом ходе поршня.

Масса воздуха в рабочей камере при движении поршня бу­дет изменяться: М = (V₀ + V)

V₀ - начальный объем рабочей полости,

V - увеличение объема полости за счет движения поршня:

Как известно, = Р / RТ. Используя данные значения V и , выражение для массы примет вид

Рассмотрим изменение массы по времени:

(6.6)

Но изменение массы по времени представляет собой массо­вый расход, поэтому выражение (6.6) может быть представлено в виде

- величина, постоянная для рассматриваемой конструкции привода, G - расход воздуха в рабочую полость; определяется согласно режимам истечения.

Данное уравнение (6.7) определяет процесс изменения дав­ления в рабочей полости при выполнении прямого хода поршня. Решение уравнения возможно при знании зависимости для пере­менной dX/dt.

6.2 Пневматический следящий привод.

Использование контурного управления для пневматического привода позволило бы решить многие проблемы и прежде всего проблему позиционирования. Однако следящий пневматический привод до настоящего времени не нашел широкого применения в практике промышленных роботов. Это определяется целым рядом обстоятельств.

Рассмотрим особенности конструкции и основные законо­мерности динамики пневматического следящего привода. На рис. 6.1 представлена принципиальная схема такого привода. В качест­ве исполнительного двигателя рассматривается цилиндр с воз­вратно - поступательным движением поршня 1. Распределителем сжатого воздуха питания является струйный механизм 2. При от­клонении струйника 2 вправо или влево пропорционально меняет­ся расход воздуха в левую или правую полость цилиндра через со­пла приемника 3. На оси струйника расположен якорь электромаг­нитного преобразователя (ЭМП). При равенстве токов управления в обмотках управления 4 имеет место равновесие сил, действую­щих на якорь; якорь и струйник находятся в среднем положении. При наличии разности токов управления равновесие сил наруша­ется, якорь и струйник поворачиваются на угол а, пропорциональ­ный разности токов. Датчиком положения штока цилиндра являет­ся потенциометр обратной связи, где напряжение между средней точкой и одной из клемм питания определяет напряжение обрат­ной связи U_ОC, пропорциональное положению штока.

Рис. 6.1

На рис. 6.2 представлена структурная схема привода. Следя­щие пневмоприводы относятся к системам дроссельного управле­ния, поскольку изменять расход на привод за счет изменения про­изводительности компрессора нецелесообразно из-за высокой сжимаемости газа.

Эквивалентная схема проточных каналов и полостей привода представлена на рис. 6.3

Расход воздуха через струйную трубку зависит от режима ис­течения и определяется следующими формулами:

- для докритического режима истечения (0,5):

- давление в полости цилиндра;

- для надкритического режима истечения при 0,5 :

Эффективные площадки наполнения и опорожнения прием­ных окон рассчитываются по формулам:

Рассмотрим вывод уравнения движения и передаточные функции пневматического привода со струйным управлением.

За неизвестную переменную примем линейное перемещение выходного звена двигателя - штока у(t), входной сигнал - пере­мещение струйной трубки h(t); t - время. При выводе линеаризо­ванного уравнения движения штока принимаются следующие до­пущения:

• динамический процесс рассматривается в окрестности уста­новившегося движения относительно среднего положения порш­ня;

• сухое трение при движении поршня пренебрежимо мало.

Движение привода оценивается двумя уравнениями: уравнением динамики выходного звена и уравнением расхода сжатого воздуха через двигатель.

Уравнение динамики:

m - масса движущихся частей (шток с поршнем +нагрузка)

F_Д - движущее усилие, приложенное к штоку;

F_Н - сила сопротивления от нагрузки;

F* - установившееся значение силы;

F- приращение силы. В этом случае

F_Д = F + F_Д;

F_н = F + F_Н;

Уравнение статики: F = F

Уравнение динамики (6.8) в приращениях будет иметь вид