
ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Задачи по комбинаторике
1.Расписание одного учебного дня состоит из шести различных дисциплин. Найти число способов составления расписания при выборе из десяти дисциплин.
2.Порядок выступления семи участников соревнований определяется жребием. Каково число различных вариантов жеребьевки?
3.В пяти номинациях кинофестиваля участвуют 10 кинофильмов. Сколько существует вариантов распределения призов?
4.В студенческой группе 25 студентов. Необходимо избрать старосту группы, ответственного за посещение занятий и организатора культурного досуга. Сколькими способами можно образовать указанную тройку, если каждый студент может занимать только один пост?
5.Четыре студента сдают экзамен. Сколько существует вариантов распределения оценок, если известно, что все студенты сдали экзамен?
6.Сколько слов длины k можно образовать, используя алфавит из n букв?
7.Сколькими способами можно обозначить треугольник, отмечая его вершины прописными латинскими буквами?
8.Сколькими способами можно расставить на шахматной доске 8 одинаковых ладей так, чтобы никакие две из них не стояли на одной горизонтали или вертикали?
9.Найти число различных (m ×n)-матриц с элементами из множества {0, 1}.
10.Найти число всех таких (m ×n)-матриц с элементами из множества {0, 1}, строки
которых попарно различны (m ≤ 2n ).
11.На книжной полке стоит собрание сочинений в двадцати томах. Сколькими способами их можно переставить так, чтобы тома 3 и 4 не стояли рядом?
12.Сколькими способами можно упорядочить числовое множество {1, 2, K, n} так,
чтобы числа 1, |
2, 3 стояли рядом и шли в порядке возрастания? |
||
13. Доказать следующие свойства биномиальных коэффициентов: |
|||
1) |
Cn0 = Cnn =1; |
3) |
Cnr =Cnn−r ; |
2) |
Cn1 = Cnn−1 = n ; |
4) |
Cnr−1 +Cnr−−11 =Cnr . |
14.Сколько разных стартовых пятерок можно образовать из двенадцати баскетболи-
стов?
15.Сколькими способами колоду из 52 карт можно разделить на две равные части?
16.При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколькими способами это можно сделать?
17.В скольких случаях при выборе из колоды в 52 листа десяти карт среди них окажутся все 4 туза?
18.Сколькими способами можно составить комиссию из трех человек, выбирая их из четырех супружеских пар так, чтобы в комиссию не входили члены одной семьи?
19.Сколько прямых линий можно провести через 8 данных точек, из которых ровно 3 лежат на одной прямой?
20.Сколько различных наборов по 8 пирожных в каждом можно составить, используя 4 различных вида пирожных?
21.Сколькими способами 10 одинаковых шаров можно разложить по четырем различным урнам, если а) ни одна из урн не должна быть пустой; б) некоторые урны могут быть пустыми?
22.Сколько существует пятизначных чисел, у которых сумма цифр равна 9 (первая цифра числа должна быть отличной от нуля)?
23. Сколько различных слов можно образовать из букв слова а) «КОЛОКОЛ»; б) «ВОДОРОД»; в) «МАТЕМАТИКА»?
24. Имеется колода из тридцати шести карт. Сколькими способами можно выбрать из этой колоды пять карт так, что среди них окажутся а) пять последовательных карт одной масти; б) четыре карты одного достоинства; в) пять карт одной масти; г) пять последовательных карт; д) три карты одного достоинства; е) две карты одного достоинства и три – других различных между собой достоинств.
Задачи на действия с событиями
25. Двое играют в шахматы. Событие A означает, что выиграл первый игрок, событие
B– выиграл второй игрок. Что означают события: а) A ; б) A + B ; в) A + B ; г) A − B ?
26.Событие A состоит в том, что хотя бы одно из имеющихся четырех изделий является бракованным; событие B – в том, что бракованных среди них не менее двух. Что оз-
начают события A − B и A B ?
27.Когда возможны равенства: а) A + B = A ; б) AB = A; в) A + B = AB ?
28.Совместны ли события A и A + B ?
29.Бросают две игральные кости. Пусть событие A состоит в том, что сумма выпавших на них очков равна 5; событие B – в том, что хотя бы на одной из костей выпала еди-
ница. Описать события AB и A B .
30. Одновременно прыгают в длину юноша и девушка. Событие A состоит в том, что юноша прыгнул дальше чем на 6 метров; событие B – в том, что юноша прыгнул дальше девушки; событие C – в том, что девушка прыгнула дальше чем на 6 метров. Что означа-
ют события ABC , A − AB ; A B C ?
31.Пусть A , B , C – произвольные события, которые могут наступить или не наступить в одном и том же эксперименте. Записать событие, состоящее в том, что:
а) произошло только событие A ;
б) произошли только события A и B ; в) произошли все три события;
г) произошло по крайней мере одно из данных событий; д) произошли по крайней мере два из данных событий; е) произошло только одно из данных событий; ж) произошло ровно два из данных событий; з) не произошло ни одно из событий; и) произошло не более двух из данных событий.
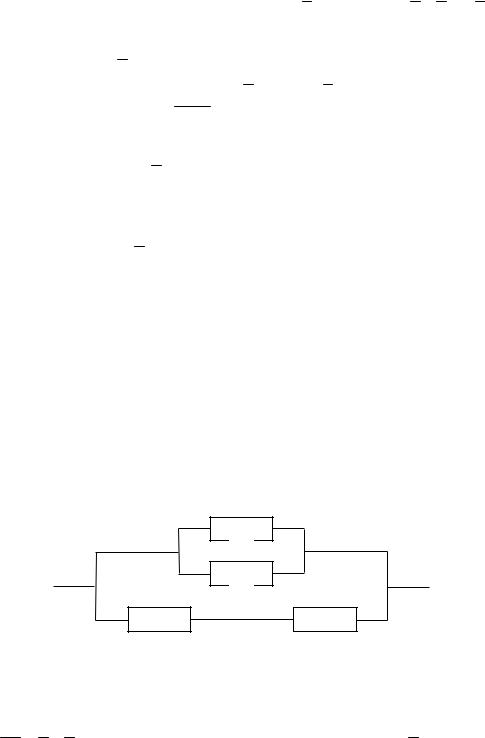
32.Имеется электрическая цепь, состоящая из четырех элементов, соединенных так, как показано на рис.1.
1 |
2 |
3 |
4 |
Рис. 1
Пусть событие Ai состоит в том, что i -ый элемент выходит из строя ( i =1, 2, 3, 4 ). За-
писать событие, состоящее в том, что цепь выйдет из строя, т.е. через нее ток не пойдет. 33. Показать справедливость следующих соотношений:
а) AB = A + B ; б) A − B = A B ;
2
в) (A − AB)+ B = A + B ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
г) (A + B)− AB = AB |
+ AB ; |
|||||||||||||||||||||||||||
д) |
|
= |
|
|
|
|
|
|
; |
е) ( |
|
|
|
)C = |
|
|
|
|
|
|
C ; |
|||||||
A + B + C |
A |
|
B |
|
C |
A + B |
A |
B |
||||||||||||||||||||
ж) ABC AB + BC + AC ; |
з) A |
|
C A + B . |
|||||||||||||||||||||||||
B |
||||||||||||||||||||||||||||
34. Упростить выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
а) (A + B)(A + |
|
); |
б) (A + B)(A + |
|
)( |
|
+ |
|
); |
|||||||||||||||||||
B |
B |
A |
B |
|||||||||||||||||||||||||
в) (A + B)(B +C); |
г) A +(B − AB)+(C − AC). |
|||||||||||||||||||||||||||
Классическое определение вероятности
35.В выпуклом двадцатиугольнике случайным образом берут 2 вершины и соединяют их отрезком. Какова вероятность того, что этот отрезок является диагональю двадцатиугольника?
36.В урне находятся 4 белых и 3 черных шара. Одновременно или последовательно, друг за другом, из урны вынимают 2 шара. Найти вероятность того, что оба шара будут белыми.
37.Участник игры «Спортлото» наудачу зачеркивает 6 клеток из 49. Найти вероятность того, что из 6 выигравших номеров он угадает: а) 3 номера; б) 4 номера; в) 5 номеров; в) все 6 номеров.
38.Из колоды, содержащей 52 листа, наудачу вынимают 10 карт. Какова вероятность того, что среди них будет хотя бы один туз?
39.Наудачу взят телефонный номер, состоящий из 6 цифр. Какова вероятность того, что все цифры номера различны?
40.Найти вероятность того, в четырехзначном числе цифра 1 содержится ровно 1 раз.
41.На полке стоят 15 книг, 5 из которых в переплете, а остальные – в мягкой обложке. Наудачу берут 3 книги. Найти вероятность того, что среди взятых книг будут: а) все 3 в переплете; б) все 3 в мягкой обложке; в) хотя бы 1 в переплете.
42.В ящике находятся 2 белых и 4 черных шара. Один за другим вынимают все имеющиеся в нем шары. Найти вероятность того, что шар, вынутый последним, будет черным.
43.На полке стоят 20 книг. Три из них убрали. Какова вероятность того, что из убранных книг никакие две не стояли рядом?
44.В ящике находятся 20 шаров с номерами 1, 2, …, 20. Наудачу берут 6 шаров. Найти вероятность того, что среди них есть шары с номерами 1 и 2.
45.Из 12 лотерейных билетов, 4 из которых выигрышные, наудачу берут 6 билетов. Какова вероятность того, что среди взятых билетов: а) хотя бы один будет выигрышным; б) ни один не будет выигрышным; в) будет ровно один выигрышный билет?
46.В течение 5 дней случайным образом поступают сообщения о банкротстве одного из 5 банков A , B , C , D , E . Чему равна вероятность того, что сообщения о банкротстве банков A и B не следуют друг за другом?
47.При наборе телефонного номера абонент забыл 2 последние цифры и набрал их наугад, помня только, что они нечетные и различные. Найти вероятность того, что номер набран правильно.
48.Найти вероятность того, что дни рождения 12 человек приходятся на разные месяцы года.
49.Бросают 4 игральные кости. Найти вероятность того, что на них выпадет одинаковое число очков.
50.Найти вероятность того, что при бросании трех игральных костей 6 очков выпадет только на одной из них, а на двух других выпадут различные между собой числа очков.
51.На шахматную доску наудачу ставят 2 ладьи: одну белого и одну черного цвета. С какой вероятностью они будут бить друг друга?
3

52.На 6 карточках написаны буквы, составляющие слово АНАНАС. Карточки перемешивают и вынимают без возврата по одной. Найти вероятность того, что карточки вынимаются в порядке следования букв данного слова.
53.На 10 карточках написаны буквы, из которых состоит слово СТАТИСТИКА. Карточки перемешивают и последовательно вынимают без возврата 4 карточки, выкладывая их в ряд. Найти вероятность того, что получится слово АИСТ.
54.В доме 9 этажей. В лифт садятся 4 пассажира, каждый из которых с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Определить вероятность того, что все пассажиры выйдут на разных этажах.
55.Из последовательности 1, 2, K, n наудачу выбирают 2 числа. Какова вероятность
того, что одно из них меньше заданного числа k , а другое – больше k (1 < k < n )?
56. Сколько раз нужно бросить игральную кость, чтобы вероятность того, что хотя бы один раз выпадет 6 очков, была не меньше: а) 0,5; б) 0,9?
Геометрическое определение вероятности
57.На плоскость с нанесенной квадратной сеткой со стороной 4 см бросают монету радиуса 1 см. Найти вероятность того, что монета не пересечет линий сетки.
58.Из отрезка [0; 1] выбрали наугад 2 числа. Какова вероятность того, что их сумма не
меньше 1, а их разность не больше 0?
59.В круг вписан квадрат. Какова вероятность того, что точка, наудачу брошенная в круг, окажется внутри квадрата?
60.На отрезке AB длины l наугад поставили 2 точки – K и M . Найти вероятность того, что точка K будет ближе к точке M , чем к точке A .
61.В течение 20 минут ученик A в случайный момент времени звонит ученику B и ждет 2 минуты, после чего кладет трубку. В течение тех же 20 минут в случайный момент времени ученик B приходит домой, где остается в течение 5 минут, после чего уходит. Какова вероятность того, что разговор состоится?
62. Наудачу выбираются 2 действительных числа x и y , причем 0 ≤x ≤1, 0 ≤ y ≤1. Найти вероятность того, что y 2 ≤ x .
63.На единичный отрезок оси абсцисс наудачу бросают точки B и C . Найти вероятность того, что длина отрезка, ограниченного этими точками, будет меньше, чем расстояние от начала координат до ближайшей точки.
64.Какова вероятность того, что сумма двух наугад взятых положительных чисел, ка-
ждое из которых меньше 1, будет не больше 1, а их произведение – не больше 92 ?
Основные теоремы теории вероятностей
65. Из генеральной совокупности, содержащей n элементов 1, 2, K, n , извлекается упорядоченная выборка объема 2 . Найти вероятность того, что вторым извлеченным элементом будет j , если первым извлеченным элементом был i (i, j {1, 2, K, n}, i ≠ j).
66.Четыре шара последовательно размещаются в четырех ячейках. Какова вероятность того, что одна из ячеек будет содержать ровно три шара, если известно, что первые два шара оказались в разных ячейках?
67.Известно, что при бросании пяти игральных костей выпала по крайней мере одна единица. Найти вероятность того, что число выпавших единиц не менее двух.
68.Буквы, составляющие слово « ПЛОТНОСТЬ», выписаны на девяти отдельных кар-
точках. Наудачу вынимают одну за другой и укладывают в ряд 4 карточки. Найти вероятность того, что получится слово « ТОСТ».
4
69.События A и B1 независимы, события A и B2 также независимы. Доказать, что если события B1 и B2 несовместны, то события A и B1 + B2 независимы.
70.Последовательно брошены три монеты. Определить, зависимы ли события:
{на первой монете выпал "герб"},
B ={хотя бы на одной монете выпала " решка"}.
71. |
Доказать, что из независимости в совокупности событий A , B и C вытекает неза- |
|||||||||||||
висимость в совокупности событий |
A |
, |
B и C ; |
A |
, |
B |
и C ; |
A |
, |
B |
и |
C |
. |
|
72. |
Доказать, что если события A , |
B и C независимы в совокупности, то события |
||||||||||||
A + B и C независимы. |
|
|
|
|
|
|
|
|
|
|
|
|||
73.Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос выдержит гарантийный срок, равна 0,95, а для полотера эта вероятность равна 0,9. Найти вероятность того, что гарантийный срок выдержат: а) оба прибора; б) только один из приборов; в) хотя бы один из приборов.
74.Устройство состоит из трех элементов, работающих независимо друг от друга. Вероятности безотказной работы за время t этих элементов соответственно равны 0,6; 0,7 и 0,8. Найти вероятность того, что в течение времени t безотказно будут работать: а) только один элемент; б) ни один из элементов; в) не менее двух элементов.
75.В пруду находятся 15 карасей и 20 карпов. Разрешается выловить 3 рыбы. Найти вероятность того, что: а) все выловленные рыбы – караси; б) все выловленные рыбы – карпы; в) все рыбы – одного вида; г) хотя бы одна из рыб – карась.
76.Какова вероятность того, что при многократном бросании игральной кости 6 очков впервые выпадет на четвертом броске?
77.Какова вероятность того, что при многократном бросании симметричной монеты «герб» впервые выпадет: а) на пятом броске; б) на нечетном броске; в) на четном броске?
78.Для того чтобы разрушить мост, требуется попадание не менее двух бомб. Независимо друг от друга сбросили 3 бомбы с вероятностями попадания соответственно 0,1; 0,3
и0,4. Найти вероятность того, что мост будет разрушен.
79.Для того чтобы сбить самолет достаточно одного попадания. Было сделано 3 независимых выстрела с вероятностями попадания соответственно 0,1; 0,2 и 0,4. Какова вероятность того, что самолет сбит?
80.Студент разыскивает нужную ему формулу в четырех справочниках. Вероятности того, что формула содержится в этих справочниках, соответственно равны 0,6; 0,7; 0,8 и 0,9. Найти вероятность того, что формула содержится: а) только в одном справочнике; б) во всех справочниках; в) только в трех справочниках.
81.Два человека поочередно бросают монету. Выигрывает тот, у кого первого выпадет «герб». Найти вероятность выигрыша для каждого игрока.
82.Вероятность попадания при каждом из трех выстрелов одинакова. Известно, что вероятность хотя бы одного попадания при трех выстрелах равна 0,875. Найти вероятность попадания при каждом отдельном выстреле.
83.Прибор содержит 4 узла: A1 , A2 , A3 и A4 . Узел A2 дублирует узел A1 , а узел A4
дублирует узел A3 . При отказе узла автоматически происходит переключение на дублирующий узел. Надежность переключающего устройства равна 0,9. Вероятности безотказной работы в течение заданного времени узлов A1 , A2 , A3 и A4 соответственно равны 0,3; 0,4; 0,5 и 0,6. Определить надежность прибора.
84.Производится несколько независимых выстрелов по мишени. Для каждого из выстрелов вероятность попадания равна 0,8. Сколько выстрелов должно быть произведено для того, чтобы вероятность хотя бы одного попадания в мишень была равна 0,99968?
85.Рассчитать вероятность отказа электрической цепи, изображенной на рис. 1, если все элементы выходят из строя независимо друг от друга и вероятность выхода из строя
элемента i равна pi ( i =1, 2, 3, 4 ).
5
