
- •Министерство образования и науки РФ ФГБОУ ВПО «Уральский государственный педагогический университет»
- •Рекомендуемая литература
- •Содержание лекции
- •§1. Введение в анализ (основные понятия)
- •§2. Числовые множества
- •§2. Числовые множества (продолжение)
- •§2. Числовые множества (продолжение)
- •§2. Числовые множества (продолжение)
- •§2. Числовые множества (продолжение)
- •§2. Числовые множества (продолжение)
- •§3. Функции 3.1. Понятие функции
- •3.1.Понятие функции (продолжение)
- •3.2. Числовые функции
- •3.2. Числовые функции (продолжение)
- •3.2.Числовые функции (продолжение)
- •3.2.Числовые функции (продолжение)
- •3.2.Числовые функции (продолжение)
- •3.2. Числовые функции (продолжение)
- •3.2. Числовые функции (продолжение)
- •3.3.Основные характеристики функций
- •3.3. Основные характеристики функций (продолжение)
- •3.3. Основные характеристики функций (продолжение)
- •3.3. Основные характеристики функций (продолжение)
- •3.4. Обратная функция
- •3.4.Обратная функция (продолжение)
- •3.4. Обратная функция (продолжение)
- •3.5. Сложная функция
- •3.6. Основные элементарные функции
- •3.6. Основные элементарные функции
- •3.6. Основные элементарные функции
- •3.6. Основные элементарные функции
- •3.6. Основные элементарные функции (продолжение)
- •3.6. Основные элементарные функции (продолжение)
- •3.6. Основные элементарные функции (продолжение)
- •3.6. Основные элементарные функции (продолжение)
- •3.6. Основные элементарные функции (продолжение)
- •3.6. Основные элементарные функции (продолжение)
- •3.6. Основные элементарные функции (продолжение)
- •3.5.Сложная функция
- •Спасибо за внимание!

3.3. Основные характеристики функций (продолжение)
Пусть функция y = f(x) определена на множестве D и пусть область D1 D.
Df: Если для любых значений аргументов x1 < x2, где x1, x2 D1, выполняется неравенство f(x1) < f(x2), то функция f(x) называется (строго) возрастающей на множестве D1; если f(x1) f(x2),
то функция f(x) называется неубывающей (нестрого возрастающей) на множестве D1.
Df: Если для любых значений аргументов x1 < x2, где x1, x2 D1, выполняется неравенство f(x1) > f(x2), то функция f(x) называется (строго) убывающей на множестве D1; если f(x1) f(x2), то
функция f(x) называется невозрастающей (нестрого убывающей) на множестве D1.

3.3. Основные характеристики функций (продолжение)
Df: Возрастающей, невозрастающие, убывающие и неубывающие функции на множестве D1 называются
монотонными на этом множестве, а возрастающие (убывающие) – строго монотонными. Интервалы, в которых функция монотонна, называются
интервалами монотонности функции.
Df: Функцию y = f(x), определенную на множестве D, называют ограниченной на этом множестве, существует такое (конечное) число M > 0, что x D выполнено неравенство |f(x)| M. Иными словами, функция y = f(x) ограничена, если ограничено множество ее значений: E(f) [ M; M].
Так, функция y = f(x) = строго монотонна на интервале ( 1; 0), где она возрастает, и на интервале (0; 1), где она убывает; функция ограничена, ибо E = [0; 1] [ 1; 1].

3.3. Основные характеристики функций (продолжение)
Df: Функция y = f(x), определенная на множестве D, называются периодической на этом множестве, если существует такое число T > 0, что x D выполняется
равенство f(x + T) = f(x) (подразумевается, что и x + T D). При этом число T называется периодом функции y
= f(x). Если T – период функции, то ее периодами будут также и числа вида nT, где n Z. Наименьшее число T, для которого выполняется равенство f(x + T) = f(x)
называется основным периодом (или просто периодом).
Так, для тригонометрической функции y = f(x) = sin x периодом являются числа вида 2 n, где n Z, ибо f(x + 2 n) = sin(x + 2 n) = sin x cos 2 n + cos x sin 2 n = sin x = f(x). Основной (наименьший положительный)
период: T = 2 .
З а д а ч а. Установить периодичность следующих функций: а) y = sin x + cos x; б) y = sin2 x; в) y = |sin x|.
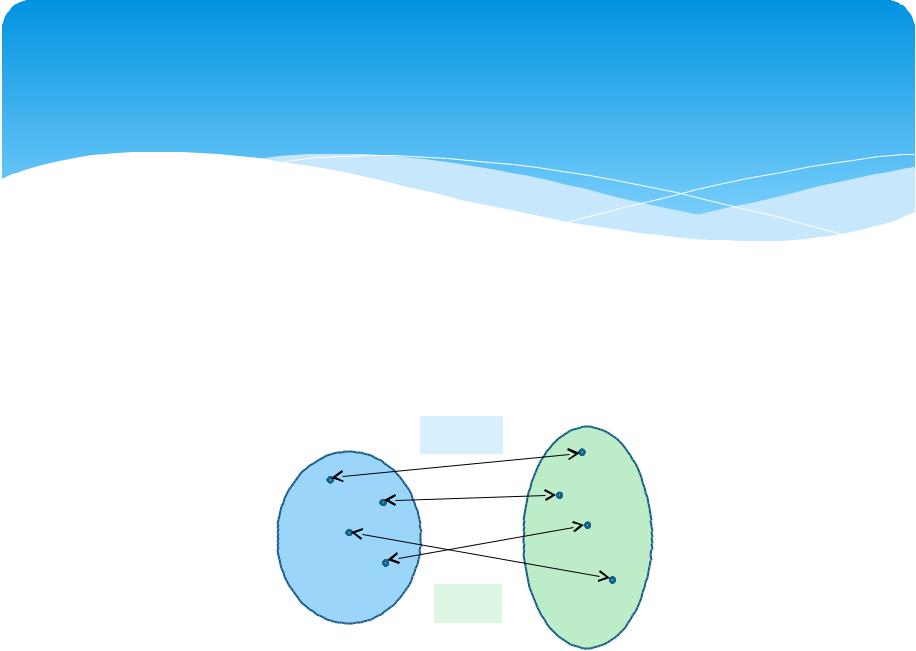
3.4. Обратная функция
Df: Пусть дана функция y = f(x) с областью определения D = D(f) и множеством значений E = E(f). Если каждому значению y E соответствует единственное значение x D, то определена функция x = (y) с областью определения D. Такая функция называется обратной к функции y = f(x). Функции f(x) и (y) являются взаимно обратными по отношению
друг к другу. Функции f(x) и (y) задают взаимно |
|
f |
множествами |
однозначное соответствие |
|
D и E.
D |
|
|
E |
|

3.4.Обратная функция (продолжение)
Чтобы найти функцию x = (y), обратную к функции y = f(x), достаточно решить уравнение f(x) = y относительно x (если это возможно), после чего
можно сделать привычное переобозначение: x y. Например, для функции y = 2x обратной является
функция x = ½ y или, после переобозначения x y, y = ½ x.
Еще. Для функции y = x2, D = [0; 1] обратной является функция x = или, после переобозначения x y, y = .
При построении обратной функции область D(f) определения исходной («прямой») функции y = f(x) для обратной функции x = (y) становится множеством значений E( ) и, наоборот, множество E(f) значений исходной («прямой») функции y = f(x) для обратной функции x = (y) становится областью определения D( ).

3.4. Обратная функция (продолжение) |
|||
Сказанное означает, что точка M1(x0; y0) |
|||
кривой прямой функции y = f(x) становится |
|||
точкой M2(y0; x0) кривой обратной функции y = |
|||
(x). Но точки M1 и M2 симметричны |
|||
относительно прямой у = x (см. рис.). |
|||
У т в е р ж д е н и е: графики взаимно |
|||
обратных функций y = f(x) и y = (x) |
|||
|
4 |
|
|
симметричны относительно биссектрисы |
|||
первого и третьегоy |
|
M1(x0; |
xy = углов. |
|
2 |
y0) |
|
|
|
|
|
f(x |
|
|
M2(y0; |
) |
00 |
|
x0) |
-2 |
2 |
4 |
|
|
|
(x |
x |
|
-2 |
) |
|
|
|
|
|

3.5. Сложная функция
Df: Пусть функция y = f(u) определена на множестве D = D(f), а функция u = (x) определена на множестве D1, причем x D1
соответствующее значение u = (x) D.
Тогда на множестве D1 определена функция y =
f( (x)) , которая называется сложной функцией
от x (или функцией f от функции или суперпозицией функций f и ).
Переменную u = (x) называют промежуточным аргументом сложной функции.
Так, функция y = sin 2x является суперпозицией двух простых (элементарных функций): y = sin u и u = 2x. Сложная функция может иметь несколько промежуточных аргументов.
3.6. Основные элементарные функции |
|||||||||
Основными элементарными функциями |
|||||||||
называют нижеследующие функции y = f(x). |
|||||||||
1. Степенная функция y = x , R. Среди |
|||||||||
степенных функций выделяется класс функций |
|||||||||
с целочисленным показателем степени: y = xn, n |
|||||||||
N. |
|
|
|
|
|
|
|
|
|
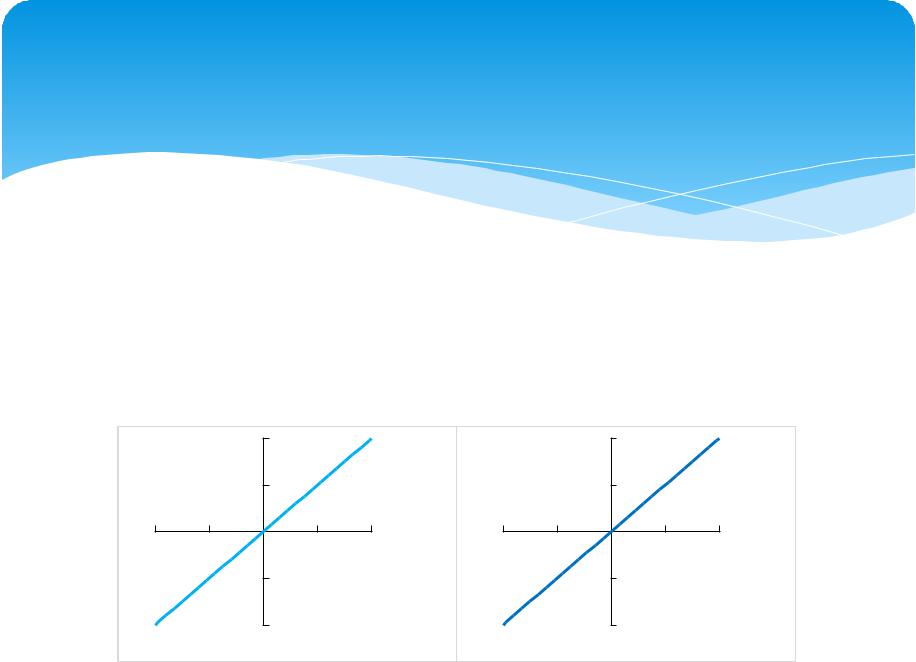
1.1. Линейная функция: y = x (см. рис., а)). |
|||||||||
Область определения D = R; множество |
|||||||||
значений: E = R; функция нечетна и монотонно |
|||||||||
а) |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
возрастаетy |
1 |
|
|
б) |
y |
1 |
|
|
|
-2 |
-1 |
00 |
1 |
2 |
-2 |
-1 |
00 |
1 |
2 |
|
|
-1 |
|
x |
|
|
-1 |
|
x |
|
|
-2 |
|
|
|
|
-2 |
|
|
3.6. Основные элементарные функции |
|||||||||||
(продолжение) |
|
|
|
|
|
|
|
|
|||
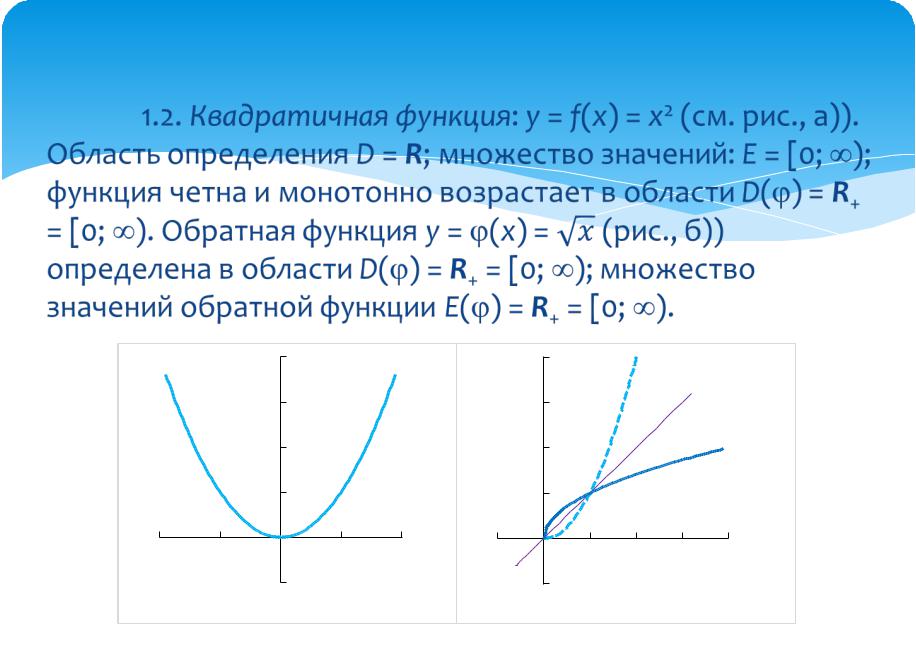
1.2. Квадратичная функция: y = f(x) = x2 (см. |
|||||||||||
рис., а)). Область определения D = R; множество |
|||||||||||
значений: E = [0; ); функция четна и монотонно |
|||||||||||
возрастает в области D( ) = R+ = [0; ). |
|
||||||||||
Обратная функция y = (x) = (рис., б)) |
|
||||||||||
определена в области D( ) = R+ = [0; ); |
|||||||||||
|
а) |
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
обратной |
|
|
б) |
= |
|||
множество |
|
|
|
|
|||||||
R+ = |
|
y |
3 |
|
|
y |
3 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
-2 |
-1 |
00 |
1 |
2 |
-1 |
00 |
1 |
2 |
3 |
4 |
|
|
|
-1 |
x |
|
|
-1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
3.6. Основные элементарные функции |
|
|
|
|||||||||
(продолжение) |
|
|
|
|
|
|
|
|
|
|||
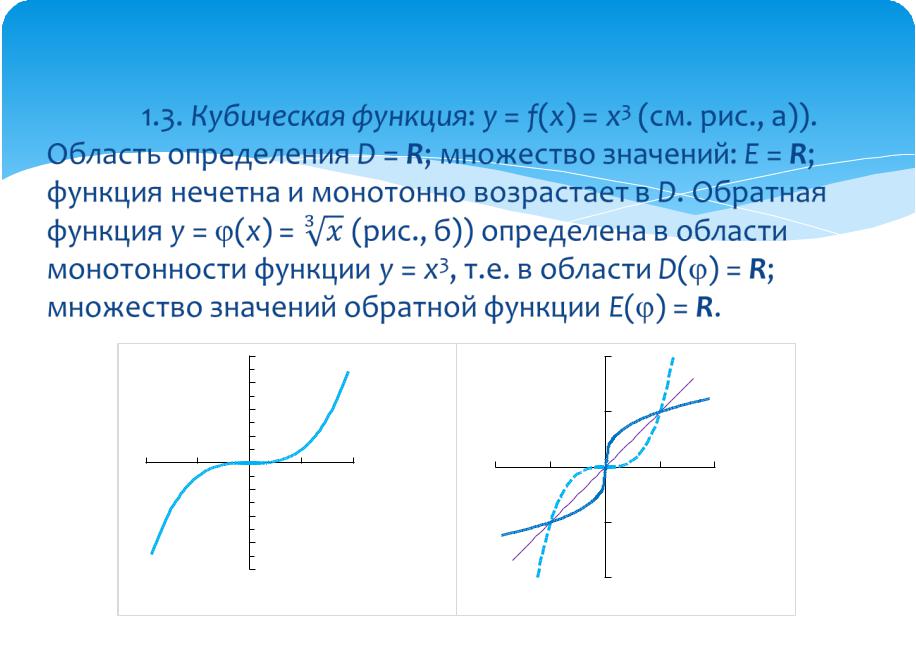
1.3. Кубическая функция: y = f(x) = x3 (см. |
|
|
||||||||||
рис., а)). Область определения D = R; множество |
||||||||||||
значений: E = R; функция нечетна и монотонно |
|
|||||||||||
возрастает в D. Обратная функция y = (x) = |
|
|
||||||||||
(рис., б)) определена в области монотонности |
|
|
||||||||||
функции y = x3, т.е. в области D( ) = R; |
E |
R |
. |
|||||||||
|
|
8 |
|
|
|
|
2 |
|
|
|||
множество значений обратной функции |
( ) = |
|
||||||||||
а) |
y |
6 |
|
|
б) |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
00 |
|
|
|
|
|
-2 |
-1 |
-20 |
1 |
2 |
-2 |
-1 |
1 |
2 |
|
|
|
|
|
|
-4 |
|
x |
|
|
-1 |
|
x |
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
