
- •Министерство образования и науки РФ ФГБОУ ВПО «Уральский государственный педагогический университет»
- •Рекомендуемая литература
- •Содержание лекции
- •§1. Исследование функций при помощи производных. Возрастание и убывание функции
- •§1. … Возрастание и убывание функции (продолжение)
- •§1. … Возрастание и убывание функции (продолжение)
- •§1. … Возрастание и убывание функции (продолжение)
- •§2. Максимум и минимум функции. Наибольшее и наименьшее значения функции на отрезке
- •§2. Максимум и минимум функции … (продолжение)
- •§2. Максимум и минимум функции … (продолжение)
- •§2. Максимум и минимум функции … (продолжение)
- •§2. Максимум и минимум функции … (продолжение)
- •§2. Максимум и минимум функции … (продолжение)
- •§2. Максимум и минимум функции … (продолжение)
- •§2. Максимум и минимум функции … (продолжение)
- •§2. … Наибольшее и наименьшее значения функции на отрезке (продолжение)
- •§2. … Наибольшее и наименьшее значения функции на отрезке (продолжение)
- •§2. … Наибольшее и наименьшее значения функции на отрезке (продолжение)
- •§2. … Наибольшее и наименьшее значения функции на отрезке (продолжение)
- •§2. … Наибольшее и наименьшее значения функции на отрезке (продолжение)
- •§3. Выпуклость графика функции. Точки перегиба
- •§3. Выпуклость графика функции. Точки перегиба
- •§3. Выпуклость графика функции. Точки перегиба (продолжение)
- •§3. Выпуклость графика функции. Точки перегиба (продолжение)
- •§4. Асимптоты графика функции
- •§4. Асимптоты графика функции (продолжение)
- •§4. Асимптоты графика функции (продолжение)
- •§4. Асимптоты графика функции (продолжение)
- •§4. Асимптоты графика функции (продолжение)
- •§4. Асимптоты графика функции (продолжение)
- •§5. Общая схема исследования функции и построения графика
- •§5. Общая схема исследования функции … (продолжение)
- •§5. Общая схема исследования функции … (продолжение)
- •§5. Общая схема исследования функции … (продолжение)
- •§5. Общая схема исследования функции … (продолжение)
- •§5. Общая схема исследования функции … (продолжение)
- •Спасибо за внимание!
§3. Выпуклость графика функции. Точки перегиба
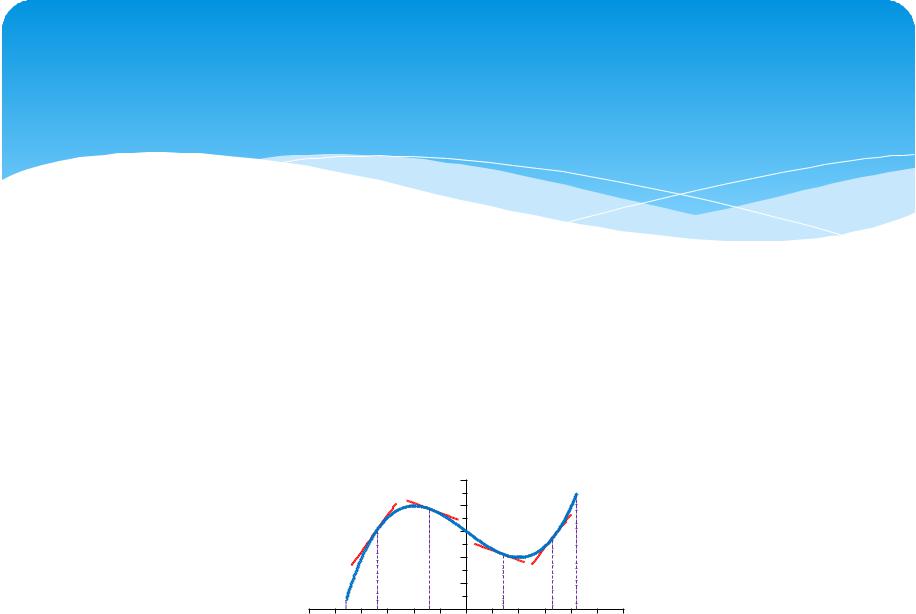
Df: График функции y = f(x) называется
выпуклым вниз (выпуклым книзу) на интервале (a; b), если он расположен выше любой ее касательной на этом интервале (см. рис.). Наоборот, график функции y = f(x) называется выпуклым вверх (выпуклым кверху) на интервале (a; b), если он расположен ниже любой ее касательной на этом интервале.
Df: Точка графика непрерывной функции y =
f(x), отделяющая |
y |
y = f(x) |
выпуклости, |
8 |
|
||
называется |
6 |
|
|
функции. |
4 |
|
|
2 |
|
|
|
|
0 |
|
|
-3 -2 |
-1 0 |
1 2 x 3 |
|

§3. Выпуклость графика функции. Точки перегиба
Интервалы выпуклости вниз и вверх находят
спомощью следующей теоремы.
Те о р е м а 6. Если дважды дифференцируемая функция y = f(x) во всех точках интервала (a; b) имеет отрицательную
вторую производную, т.е. f (x0) < 0, то график
функции в этом интервале выпуклый вверх. Если же f (x0) > 0 x (a; b) – график выпуклый
вниз.
Доказательство: СРС.

§3. Выпуклость графика функции. Точки перегиба (продолжение)
Для нахождения точек перегиба графика функции используется следующая теорема.
Т е о р е м а 7 (достаточное условие существования точек перегиба). Если у дважды дифференцируемой функции y = f(x) 2-ая производная f (x0) при переходе через точку x0, в которой она равна
нулю или не существует, меняет знак, то точка графика с абсциссой x0 есть точка перегиба.
Доказательство: Пусть f (x) < 0 при x < x0 и f (x) > 0 при x > x0. Это значит, что слева от точки x = x0 график
выпуклый вверх, а справа – выпуклый вниз. Следовательно, точка (x0; f(x0)) графика является
точкой перегиба, ч.т.д.
Аналогично доказывается, что если f (x) > 0 при x <
x0 и f (x) < 0 при x > x0, то точка (x0; f(x0)) точка перегиба.

§3. Выпуклость графика функции. Точки перегиба (продолжение)
П р и м е р 7. Исследовать на выпуклость и точки перегиба график функции y = x3 3x + 6.
Решение: Найдем первую и вторую производные функции и приравняем последнюю нулю:
y = (x3 3x + 6) = 3x2 3 = 3(x2 1).
y = 6x = 0 при x0 = 0.
Ясно, что y < 0 при x < 0, здесь график функции y(x) выпуклый вверх, и y > 0 при x > 0, здесь график функции y(x) выпуклый вниз. Точка x0 = 0 – точка перегиба.
Ответ: Точка x0 = 0 – точка перегиба (см. график на первом слайде §3).
§4. Асимптоты графика функции |
||
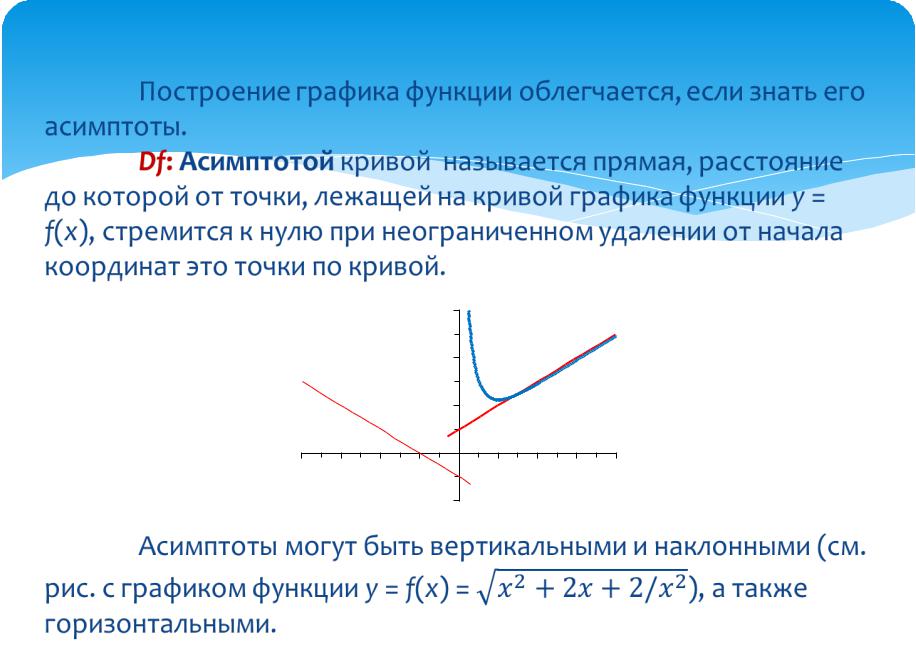
Построение графика функции облегчается, если |
||
знать его асимптоты. |
|
|
Df: Асимптотой кривой называется прямая, |
||
расстояние до которой от точки, лежащей на кривой |
||
графика функции y = f(x), стремится к нулю при |
||
неограниченном удалении от начала координат это |
||
точки по кривой |
y 6 |
y = f(x) |
|
|
|
|
4 |
|
|
2 |
|
|
0 |
1 2 3 4 |
|
-4 -3 -2 -1 0 |
|
|
-2 |
x |
|
|
|
Асимптоты могут быть вертикальными и |
||
наклонными (см. рис. с графиком функции y = f(x) = ), |
||
а также горизонтальными. |
|
|

§4. Асимптоты графика функции (продолжение)
Df: Говорят, что прямая x = a является
вертикальной асимптотой графика функции y
= f(x), если = , или = , или = .
Правило отыскания вертикальных асимптот:
Для отыскания вертикальных асимптот графика функции y = f(x) следует найти те значения x, вблизи которых функция f(x) по модулю неограниченно возрастает. Обычно такие точки являются точками разрывов второго рода.
Так, кривая функции y = имеет вертикальную асимптоту x = 1, ибо = и = + .
§4. Асимптоты графика функции (продолжение)
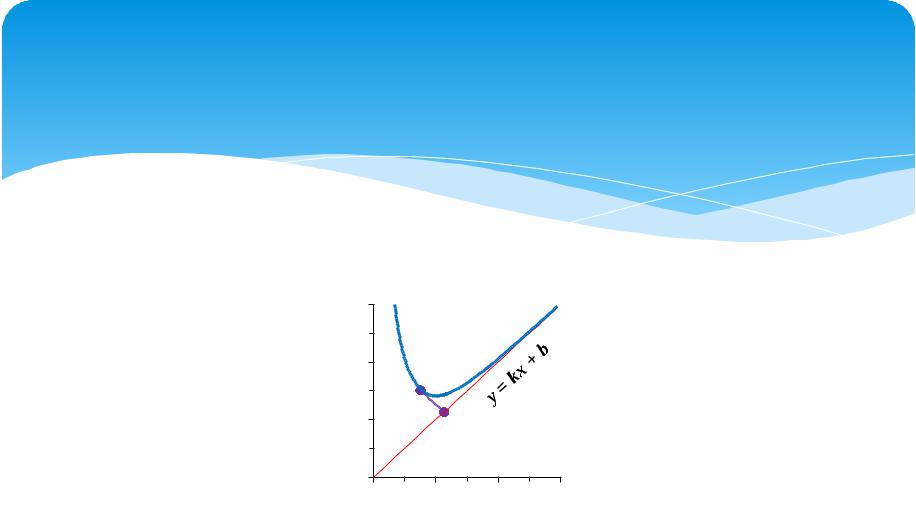
Df: Если уравнение асимптоты имеет вид y = kx + b, где k – конечное число, то говорят, что эта прямая является наклонной асимптотой графика функции y = f(x) (см. рис.); в частности, если k = 0, то говорят о горизонтальной асимптоте к
графику функции y = f(x).
3 |
|
|
|
y = f(x) |
y |
|
|
|
|
|
|
|
|
|
2 |
M(x; y) |
|
|
|
1 |
d |
N |
|
|
|
|
|
||
|
|
|
|
|
0 |
|
1 |
2 |
3 |
0 |
|
|||
|
|
|
|
x |
Итак, будем искать уравнение наклонной асимптоты к графику функции y = f(x) в виде y = kx + b. Найдем k и b.

§4. Асимптоты графика функции (продолжение)
Пусть M(x; y) – произвольная точка кривой y = f(x). Из аналитической геометрии на плоскости известно, что расстояние от точки M(x; y) до прямой y = kx + b дается выражением: d = .
Для наклонной асимптоты параметр k является конечным числом, поэтому условие d 0 при x выполняется, если к нулю стремится числитель дроби:
= 0. Отсюда следует, что разность под знаком модуля может быть представлена в виде kx y + b = , где = (x) – б.м.ф., т.е. 0 при x. Разделив обе части равенства kx y + b = на x и переходя к пределу при x , получим:
= = k.

§4. Асимптоты графика функции (продолжение)
Выразив угловой коэффициент асимптоты k: k = ,
получим затем выражение для свободного члена b: b = .
Правило отыскания наклонных асимптот:
Для отыскания наклонных асимптот y = kx + b графика функции y = f(x) необходимо последовательно вычислить коэффициенты асимптоты по формулам:
k = , b = .
За м е ч а н и е: Асимптоты функции y(x) при x
и x могут быть, вообще говоря, различными. Поэтому необходимо рассматривать
оба случая x .

§4. Асимптоты графика функции (продолжение)
П р и м е р 8. Найти асимптоты функции y = x(ex1).
Решение: Действуя по указанному выше правилу отыскания наклонных асимптот, найдем k и b:
k+ = = = = ,
k = = = = -1 + = -1.
Т.о., при x асимптоты нет, а при x
угловой коэффициент k = 1. Для этого случая найдем свободный член:
b = = = = 0.
У графика функции y = x(ex 1) при x имеется наклонная асимптота y = x.
Ответ: У графика функции y = x(ex 1) при xимеется наклонная асимптота y = x; при x + асимптоты нет.
