
- •Министерство образования и науки РФ ФГБОУ ВПО «Уральский государственный педагогический университет»
- •Рекомендуемая литература
- •Содержание лекции
- •§1. Задачи, приводящие к понятию производной
- •§1. Задачи, приводящие к понятию производной (продолжение)
- •§1. Задачи, приводящие к понятию производной (продолжение)
- •§1. Задачи, приводящие к понятию производной (продолжение)
- •§1. Задачи, приводящие к понятию производной (продолжение)
- •§2. Определение производной; ее механический и геометрический смысл. Дифференцируемость. Уравнение касательной и нормали
- •§2. Определение производной … (продолжение)
- •§2. Определение производной … (продолжение)
- •§2. Определение производной … (продолжение)
- •§3. Связь между непрерывностью и дифференцируемостью функции
- •§3. Связь между непрерывностью и дифференцируемостью функции (продолжение)
- •§3. Связь между непрерывностью и дифференцируемостью функции (продолжение)
- •§4. Производная суммы, разности, произведения и частного функций
- •§4. Производная суммы, разности, произведения
- •§4. Производная суммы, разности, произведения
- •§4. Производная суммы, разности, произведения
- •§5. Производные сложной и обратной функций
- •§5. Производные сложной и обратной функций (продолжение)
- •§5. Производные сложной и обратной функций (продолжение)
- •§5. Производные сложной и обратной функций (продолжение)
- •§6. Производные основных элементарных функций
- •§6. Производные основных элементарных функций (продолжение)
- •§6. Производные основных элементарных функций (продолжение)
- •§6. Производные основных элементарных функций (продолжение)
- •§6. Производные основных элементарных функций (продолжение)
- •§6. Производные основных элементарных функций (продолжение)
- •§6. Производные основных элементарных функций (продолжение)
- •§7. Таблица производных
- •§7. Таблица производных (продолжение)
- •Спасибо за внимание!

Министерство образования и науки РФ ФГБОУ ВПО «Уральский государственный педагогический университет»
Математический факультет Кафедра высшей математики
Математика
Лекция 6. Производная функции
Лектор: Бодряков В.Ю. E-mail: Bodryakov_VYu@e1.ru Поток: 1 к. ИКРиМ, 2012-2013 уч.г.
Екатеринбург - 2012

Рекомендуемая литература
1.Берман Г.Н. Сборник задач по курсу математического анализа: учеб пособие. СПб.: Лань, 2007. – 448 с.
2.Письменный Д.Т. Конспект лекций по высшей математике: [в 2 ч.]. Ч. 1. – М.: Айрис – Пресс, 2008. – 288 с.
3.Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа: учебное пособие для вузов. М.: БИНОМ. Лаборатория знаний, 2009. – 672 с.
4.Фихтенгольц Г.М. Основы математического анализа. Ч. 1. СПб.: Лань, 2005. – 448 с., Ч.2, 2005. – 464 с.
5.Электронный ресурс: www.exponenta.ru

Содержание лекции
§1. Задачи, приводящие к понятию производной
§2. Определение производной; ее механический и геометрический смысл. Дифференцируемость. Уравнение касательной и нормали к кривой
§3. Связь между непрерывностью и дифференцируемостью функции
§4. Производная суммы, разности, произведения и частного функций
§5. Производные сложной и обратной функций
§6. Производные основных элементарных функций
§7. Таблица производных
§1. Задачи, приводящие к понятию производной
Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики и др. наук, в особенности при изучении скорости протекания различных процессов.
Скорость прямолинейного движения |
||||
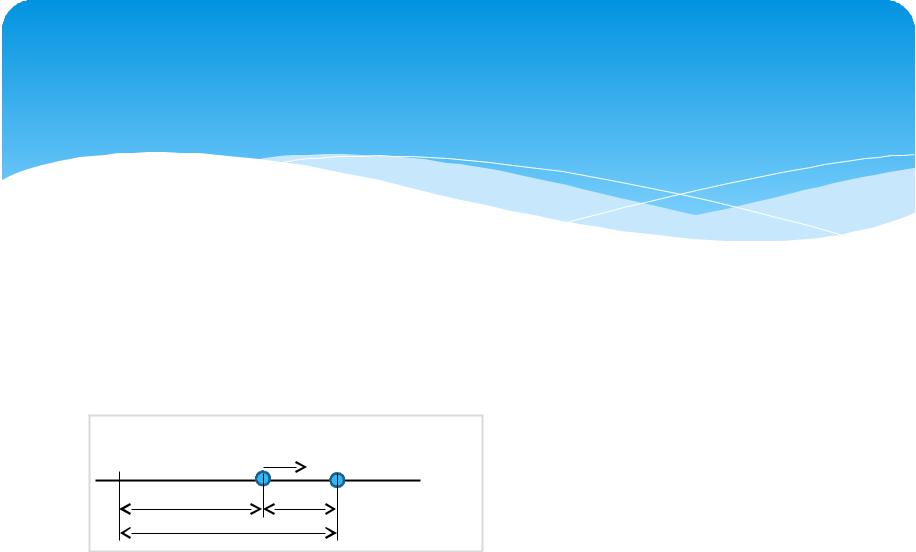
Пусть материальная точка (м.т.) M движется |
||||
вдоль некоторой прямой ℓ (см. рис.). Положение |
||||
т. MO можноM v |
M |
ℓ |
охарактеризовать |
|
S(t |
|
S |
|
|
|
расстоянием OM = S(t) до |
|||
точки))S(t+ t |
отсчета |
O. |
||
Уравнение |
S |
= S(t) |
называется |
|
уравнением или законом движения м.т. |
||||

§1. Задачи, приводящие к понятию производной (продолжение)
Если в некоторый момент времени t точка занимает положение M, то в момент времени t + t, где t – приращение времени, точка займет новое положение M , так что расстояние от него до точки отсчета составит OM = S(t + t) = S(t) + S, где S – приращение расстояния. Т.о., перемещение т. M за время t составит S = S(t + t) S(t).
Df: Средней скоростью движения м.т. за времяt называется отношение приращения расстоянияS к приращению времени t: Vср = .
Df: Предел средней скорости м.т. при t 0 называется мгновенной скоростью V и
выражается как
V = = .
Говорят, что скорость есть производная пути S(t).

§1. Задачи, приводящие к понятию производной (продолжение)
Касательная к кривой
Дадим общее определение касательной к кривой.
Возьмем на непрерывной кривой L две точки M и M1 (см. рис.). Прямую ММ1, проходящую через эти
точки, называют секущей. Пусть точка M1, двигаясь вдоль кривой L, неограниченно приближается к
точке M (можно сказать, что M = , Mn L). Тогда |
|||||
секущая, поворачиваясь около точки M, стремится к |
|||||
некоторому предельному положению – прямой MT. |
|||||
T |
|
|
в данной |
точке M |
|
M |
|
|
|||
Df: Касательной3 |
|||||
|
M2 |
M |
|
положение MT секущей |
|
называется предельное |
|||||
|
|
1 |
|
|
|
MMn, M когда 2-я точка пересечения, т.е. Mn, |
|||||
|
|
L |
|
|
кривой к точке M, |
неограниченно стремится по |
|||||
т.е. при Mn |
|
M (n ). |
|
|
|
§1. Задачи, приводящие к понятию производной (продолжение)
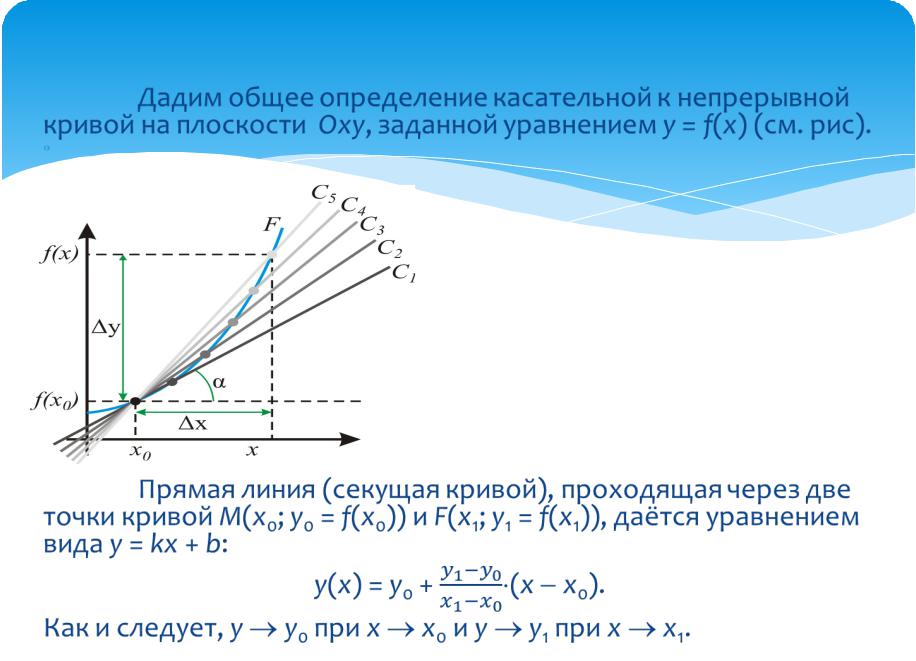
Дадим общее определение касательной к непрерывной кривой на плоскости Oxy, заданной уравнением y = f(x) (см. рис).
Прямая линия (секущая кривой), проходящая через две точки кривой M(x0; y0 = f(x0)) и F(x1; y1 = f(x1)), даётся уравнением вида
y = kx + b:
y(x) = y0 + (x x0).
Как и следует, y y0 при x x0 и y y1 при x x1.

§1. Задачи, приводящие к понятию производной (продолжение)
Угловой коэффициент (тангенс угла наклона) секущей определяется как
k = .
По мере того, как точка x1, двигаясь вдоль кривой y = f(x), приближается к точке x0, т.е. при x1 x0,
угловой коэф-т k секущей стремится к некоторому своему предельному значению
k0 = tg = = = y (x0). Здесь обозначено x = x1 x0.
Df: Прямая линия с угловым коэффициентом k0,
предельная для семейства секущих, называется касательной к кривой y = f(x) в точке x0.
Говорят, что угловой коэффициент касательной k0 = = tg есть производная зависимости y = f(x).

§2. Определение производной; ее механический и геометрический смысл. Дифференцируемость. Уравнение касательной и нормали к кривой
Пусть функция y = f(x) определена на некотором интервале D = (a; b). Дадим абсциссе x0 (a; b)
малое приращение x такое, что x0 + x (a; b). Вычислим приращение функции y = f(x0 + x) f(x0). Величина предела отношения приращения
функции к приращению аргумента при x 0 играет важную роль в анализе.
Df: Производной функции y = f(x) в точке x0
называется предел отношения приращения функции y к приращению аргумента x при x 0:
y (x0) = = = f (x0).
Производную функции в т. x, если она существует обозначают также как: fx , yx , , .

§2. Определение производной … (продолжение)
Df: Функция y = f(x), имеющая производную в каждой точке некоторого интервала (a; b), где она определена, называется дифференцируемой в (на) интервале (a; b); операция вычисления производной функции называется ее дифференцированием.
Врезультате дифференцирования функции y
=f(x) получается производная функция y = f (x).
Значение производной функции y = f (x) в точке x0 обозначается как: f (x0), y (x0), .
П р и м е р 1. Найти производные функций: а) y = C = Const; б) y = x; в) y = x2.
Решение: а) y (x) = 0; б) y (x) = = 1; в) y (x)
= = = 2x.
