2.8. Приближенный алгоритм нахождения кратных медиан графа

Тэйц и Барт предложили эвристический метод для нахождения р-медианы. Метод состоит в следующем: случайным образом выбираются р вершин, они и образуют начальное множество S, аппроксимирующее р-медианное множество . Затем выясняется, может ли некоторая вершиназаменить вершину, для чего строится новое множествои сравниваются передаточные числа и . Если , то вершина замещается вершинойи из множестваS получается множество , которое лучше аппроксимирует р-медианное множество . Затем исследуется и преобразуется множество , по вышеприведенной процедуре до тех пор, пока не будет построено множество , такое, что ни одну его вершину нельзя заместить вершинной из множестваи получить множество с меньшим передаточным числом, чем . Множество S^* берется в качестве требуемого приближения к множеству .

Описание приближенного алгоритма:

Шаг 1. Выбрать некоторое множество S из р вершин в качестве начального приближения к р-медиане. Назовем все вершины "неопробованными".

Шаг 2. Взять произвольную «неопробованную» вершину и для каждой вершины вычислить "приращение", соответствующее замене вершинывершиной, т.е. вычислить

.

Шаг 3. Найти .

1. Если , то назвать вершину"опробованной".

2. Если , тои назвать все вершины множества"неопробованными".

Шаг 4. Если все вершины из множества опробованы, то конец алгоритма (текущее множествоS является аппроксимацией р-медианного множества ), иначе перейти к шагу 2.

Этот алгоритм можно применить для нахождения р-центра.

2.9. Практическое применение задачи размещения медиан

В ряде задач о размещении пунктов обслуживания требуется так расположить обслуживания на графе, чтобы сумма кратчайших расстояний от этого пункта до вершин графа была минимально возможной. Оптимальное в указанном смысле место расположения пункта называется медианой графа. Исходя из природы целевой функции, такие задачи называют минисуммными задачами размещения. Эти задачи в различных формах часто встречаются на практике: при выборе места расположения коммутаторов в телефонной сети, подстанций в электросетях, баз снабжения в сети дорог, отделов сортировки в почтовой связи и т.д.

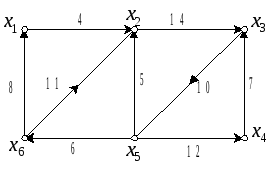
3. Задание

3.1. Получить у преподавателя вариант задания.

3.2. Для графа G с весами вершин заданными вектором V найти центр, абсолютный центр ("искусственные точки" выбрать посередине каждого ребра) и p-центры (p=2, 3 и 4).

3.3. Для графа G с весами вершин заданными вектором V найти медиану и p-медианы (p=2, 3 и 4).

Варианты задания:

№ варианта	№ графа	V
1	1	[5,3,1,7,4,6]
2	2	[4,2,8,2,5,4]
3	3	[7,6,4,5,8,3]
4	4	[6,4,6,6,7,1]
5	5	[2,3,5,4,3,2]
6	6	[8,7,1,8,1,5]
7	1	[9,8,9,3,2,6]
8	2	[1,6,2,9,4,7]
9	3	[3,7,4,7,1,9]
10	4	[5,3,2,6,5,6]
11	5	[7,9,1,4,4,8]
12	6	[9,1,3,1,7,6]

1. 2.

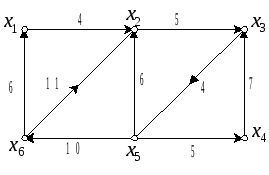
3. 4.

5. 6.