Применение к сетевому планированию и управлению
Допустим,
что нужно реализовать некий проект,
состоящий из большого числа этапов. Мы
можем изобразить каждый этап вершиной
некоторого графа и построить дугу от
вершины
к вершине
,
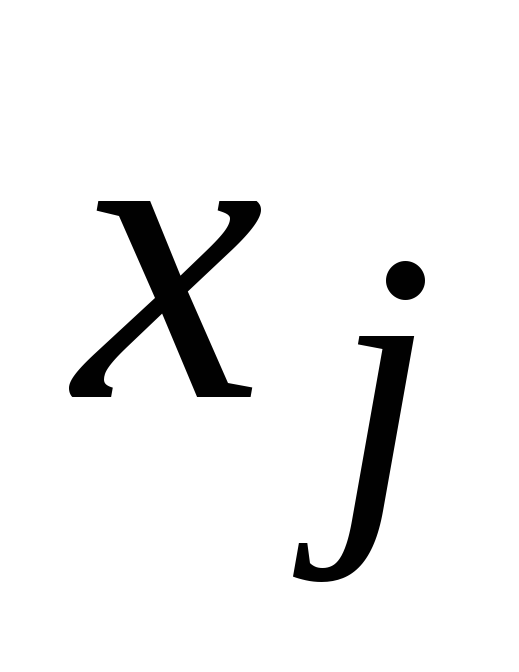чтобы показать, что этап i
должен предшествовать этапу j.
Каждой дуге приписывается некоторый
вес
,
равный минимальной задержке во времени
между началом этапа i
и началом этапа j.
В задаче требуется найти минимальное время, необходимое для реализации проекта. Иными словами, нужно найти в графе самый длинный путь между вершиной s, изображающей начало, и вершиной t, изображающей завершение всех необходимых для реализации проекта работ. Самый длинный путь называется критическим путем, так как этапы, относящиеся к этому пути, определяют полное время реализации проекта, и всякая задержка с началом выполнения любого из этих этапов приведет к задержке выполнения проекта в целом.
Данную задачу можно решить как задачу нахождения кратчайшего пути, используя алгоритм Дейкстры, заменив операцию min на max.