5. Подграфы

Пусть дан граф G=(X, А). Остовным подграфом G_p графа G называется граф (X, А_р), для которого . Таким образом, остовный подграф имеет то же самое множество вершин, что и граф G, но множество дуг подграфа G_p является подмножеством множества дуг исходного графа.

Граф на рис. 1.4(б) — остовный подграф G_p графа G, изображенного на рис. 1.4(а).

Пусть дан граф G = (X, Г). Порожденным подграфом ²) G₃, называется граф , для которогои для каждой вершины. Таким образом, порожденный подграф состоит из подмножества вершин множества вершин исходного графа и всех таких дуг графа G, у которых конечные и начальные вершины принадлежат подмножеству X₃. Часто бывает удобно обозначать подграф G₃ просто символом ; мы будем в дальнейшем использовать такое обозначение, если нет опасности внесения путаницы.

На рис. 1.4(в) показан порожденный подграф графа, приведенного на рис. 1.4(а), содержащий только вершины и дуги, которые их связывают.

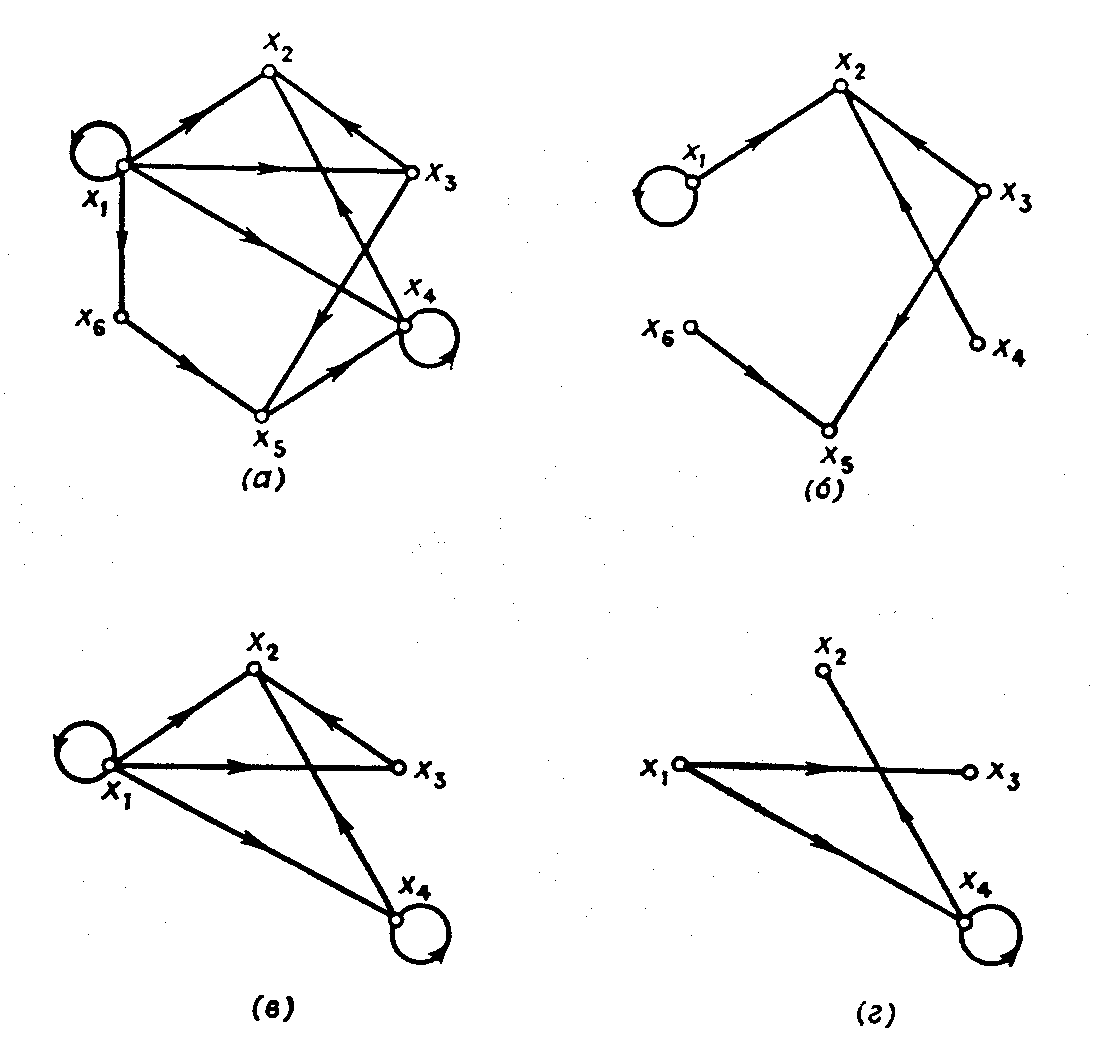
Рис. 1.4. (а) Граф, (б) Остовный подграф, (в) Порожденный подграф, (г) Подграф.

Соединяя приведенные выше два определения, можно сформулировать определение подграфа. Граф, показанный на рис. 1.4(г), является подграфом графа, приведенного на рис. 1.4(а).

Рассмотрим граф, вершины которого представляют сотрудников некоторого учреждения, а дуги — линии связи между сотрудниками. Тогда граф, представляющий только наиболее важные каналы связи данного учреждения, является остовным подграфом; граф, который подробно представляет линии связи только какой-то части этого учреждения (например, отделения), является порожденным подграфом, а граф, который представляет только важные линии связи в пределах отделения, является подграфом.

6. Типы графов

Граф называют полным, если для любой пары вершин и в X существует ребро в , т. е. для каждой пары вершин графа G должна существовать по крайней мере одна дуга, соединяющая их. Полный неориентированный граф, построенный на п вершинах, обозначается через К_п.

Рис. 1.5 (а) Симметрический граф, (б) Антисимметрический граф, (в) Полный симметрический граф, (г) Полный антисимметрический граф.

Граф (X, А) называется симметрическим, если в множестве дуг А для любой дуги существует также противоположно ориентированная дуга .

Антисимметрическим графом ¹) называется такой граф, для которого справедливо следующее условие: если то в множестве А нет противоположно ориентированной дуги, т. е. . Очевидно, что в антисимметрическом графе нет петель.

На рис. 1.5(а) показан симметрический граф, а на рис. 1.5(б)-антисимметрический граф.

Рассмотрим следующий пример: множество вершин графа представляет группу людей, дуга, направленная от вершины к вершине , означает, что , является другом или родственником , тогда данный граф должен быть симметрическим. С другой стороны если дуга, направленная от к означает, что вершина , подчинена вершине , то такой граф должен быть антисимметрическим.

Комбинируя приведенные выше определения, можно дать определения полного симметрического графа (пример такого графа см. на рис. 1.5(в)) и полного антисимметрического графа (один из таких графов показан на рис. 1.5(г)). Граф последнего типа часто называют также турниром.

Неориентированный граф G=(X, А) называют двудольным, если множество его вершин X может быть разбито на такие два подмножества Х^а и Х^b, что каждое ребро имеет один конец в Х^а,с другой в Х^b. Ориентированный граф G называется двудольным, если его неориентированный двойник —двудольный граф. Легко доказать следующее утверждение.

Теорема 1. Неориентированный граф G является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины.

Если нужно подчеркнуть, что граф является двудольным, то для графа применяют обозначение , подразумевая, что выполняются также соотношения (1.13).

Двудольный граф называют полным, если для любых двух вершин существует ребро . Если —число вершин множества—равноr и , то полный неориентированный двудольный граф обозначается через .

Граф G=(X, А) называется планарным, если он может быть нарисован на плоскости (или сфере) таким образом, что произвольные две дуги графа не пересекаются друг с другом. На рис. 1.6(а) показан полный граф К₅, а на рис. 1.6(б)—полный двудольный граф К_3,3, которые являются непланарными.

Рис. 1.6. Непланарные графы Куратовского. (a) K₅. (б) K_3,3.