19. Понятие связей в исследованиях. Типы. Способы описания

Все явления и процессы взаимосвязаны. Особенность связей в экономике и социальных сферах состоит в том, что их закономерный характер проявляется лишь в массе явлений. Проблема исследования связей является одной из важнейших проблем в экономике.

Переменные могут быть связанны функциональной или статистической зависимостями, либо вообще быть независимыми. Функциональная –зависимость, при которой каждому значению факторной переменной «х» соответствует определенное значение результативной переменной «у». Строгая функциональная зависимость встречается редко, так как переменные подвержены влиянию случайных факторов.

Статистической называют зависимость, при которой изменения одной переменной влечет за собой распределение другой. Частный случай статистической зависимости - это корреляционная зависимость, когда изменение одной переменной, влечет за собой изменение среднего значения другой. Задача корреляционного анализа состоит в измерении тесноты связи между признаками и выявления факторов, которые оказывают на них наибольшее влияние.

Задача регрессионного анализа заключается в выборе типа модели, то есть формы связи устанавливающей степень влияния переменных.

Причинно следственная связь факторных и результативных признаков характеризуется: Степенью тесноты; Направлением; Аналитическим выражением

20.Кореляционный анализ. Оценка степени связи явлений….

Корреляционный анализ позволяет установить тесноту связи между факторами и решить задачи: 1.определить существование или отсутствие связи; 2.выявить изменение связи в различных ситуациях; 3.определить наиболее значимые факторы, влияющие на результативный признак. Парная корреляция – зависимость между результативным и факторным признаком. Частная корреляция – зависимость между результативным признаком и одним фактором, при фиксированном значении других факторов. Множественная корреляция – зависимость результативного признака от нескольких факторов. Поле корреляции - совокупность точек, каждая из которых соответствует отдельной единицы совокупности, а координаты точек определяются значениями признаков «х» и «у».

Связь отсутствует Связь прямая лин. Связь обратная лин. Нелнейн.связь

Показателем тесноты связи: Линейный коэффициент корреляции; Множественные коэффициенты; Коэффициент корреляции знаков

21. Коэф-т корреляции, проверка значимости

Чем ближе к 1 тем связь теснее, если r стремится к 0 то связь отсутствует.

Коэф-т корреляции	Характеристика связи
|r|<0.3	Слабая
|r|=0.3 . . 0.7	Средняя
|r|>0.7	Сильная(Тесная)
|r|=1	Функциональная
r=0	Отсутствует

r < 0 – связь обратная, r > 0 – связь прямая

Значимость оценивается на основе t-критерия Стьюдента.

1.при заданном уровне значимости () выдвигается гипотеза Но:r=0, т.е. связь между признаками отсутствует.

2.выбираем в качестве критерия t_РАССЧ ; число степеней свободы

3.по таблице критических значений t Стьюдента находят t_КРИТ и сравнивается с найденным значением.

4.если t_РАССЧ < t_КРИТ то гипотеза принимается, то есть связь между х и у действительно отсутствует.

5.если t_РАССЧ > t_КРИТ то Hо отвергается, то есть связь между изучаемыми признаками является существенной.

22. Регрессионный анализ – метод статистического анализа зависимости случайной величины от переменных x_j(j=1,2…k), рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения x_j. Построить уравнение регрессии значит найти его параметры, в нашем случае А и В. – метод наим. квадратов

Идентификация регрессии, то есть определение ее параметров А и В осуществляется на основе метода наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений теоретических значений результативного признака от его эмпирических(данные полученные в ходе исследования) значений.

В результате решения этих систем получается система нормальных уравнений для нахождения параметров А и В. Система разрешима и имеет единственное решение. Это решение состоит в том чтобы определить искомые параметры А и В.,

23. После того как определены параметры модели регрессии А и В, необходимо оценить их значимость, то есть существенность. Оценка значимости параметров осуществляется с использованием t-критерия Стьюдента.

Алгоритм:1. При заданном уровне значимости выдвигается гипотеза Но: r=0, т.е. связь между признаками x и y отсутствует.

2. Выбираем в качестве критерия величину t_рассч. Число степени

3. По таблице критических значений t Стьюдента находят t_{критич.} и сравнивается с найденным значением.

4. Если t_рассч. < t_{критич.} то гипотеза принимается, то есть связь между х и у действительно отсутствует.

5. Если t_рассч. > t_{критич.} то нулевая гипотеза отвергается, то есть связь между изучаемыми признаками является существенной.

Коэффициент R² используется для оценки качества построенного регрессионного уравнения. такая проверка осуществляется на основе F – критерия Фишера.

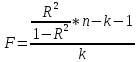
Алгоритм проверки значимости регрессии в целом(адекватности модели):1.Для уровня значимости и числа степеней свободы и найти F_рассч.

2.по таблице критических значений F –критерия Фишера найти F_{критич.}

3.F_{критич.}>F_{расчетн.}, => регрессионная модель в целом не значима

F_{расчет.} >F_{критич.} => в целом данная модель значима и пригодная для принятия управленческих решений, т.е. анализа и прогнозирования

24. Эмпирический коэффициент детерминации показывает долю вариации результативного признака, обусловленную вариацией группировочного признака:

Эмпирическое корреляционное отношение есть показатель тесноты связи между группировочным и результативными признаком: , [0;1]

1. =1 => =0, т.e. вариация результативного признака полностью обусловлена вариацией группировочного признака, т.e. между ними существует функциональная зависимость.

2. =0 => , т.е. общая дисперсия будет равна средней, то есть вариация результативного признака не зависит от вариации группировочного признака, то между ними нет корреляционной связи.

25. Социально-экономический процесс - изменения в обществе, которые отражаются на его благосостоянии, политической и экономической стабильности, условиях безопасности и прочем. Эти процессы тесно привязаны к деятельности предприятий, крупных национально-государственных систем и регионов, что определяет масштабы, уровень, темпы и цели происходящего в русле этих, постоянно меняющихся, объектов. Для прогнозирования социально-экономических процессов существуют три основных класса моделей: модели временных рядов, системы эконометрических уравнений и регрессионные модели. Наиболее точным является последний класс, потому что в отличие от других средняя ошибка (доверительный интервал) прогноза рассчитывается с достаточно большой надежностью.

Точечный прогноз заключается в получении прогнозного значения у_p, которое определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения x_p Интервальный прогноз заключается в построении доверительного интервала прогноза, т. е. нижней и верхней границ у_pmin , у_pmax интервала, содержащего точную величину для прогнозного значения ŷ_p (у_pmin < ŷ_{p <} у_pmin). Доверительный интервал всегда определяется с заданной вероятностью (степенью уверенности), соответствующей принятому значению уровня значимости

26. Ряды динамики – это статистические данные отображающие развитие изучаемого явления во времени.

Типы:1)Моментные ряды отображают состояния изучаемых явлений на определенные даты.2)Интервальные ряды отображают итоги развития явлений в процессов за отдельные периоды. 3)Производственные ряды – это такие ряды, уровни которых представляют собой не непосредственно наблюдения, а некие производственные величины(относительные, средние).

Для количественной оценки динамики социальных процессов применяются следующие статистические показатели:

1.Абсолютный прирост -базисныйцепной,

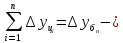Сумма цепных абсолютных приростов равна базисному абсолютному приросту, рассчитанному за весь период в целом

2.Темпы роста – базисный, –цепной

-Произведение цепных темпов роста равно базисному темпу роста, рассчитанному за весь период

3.Темп прироста - базисный, –цепной

4.Темпы наращивания