
MATLAB_03
.pdf
11
>> plot(x,y1,x,y2), grid, xlabel ('x'), legend('sin(x)','sqrt(x)')
6 |
|
|
|
|
|
|
|
|
|
|
|
|
sin(x) |
5 |
|
|
|
|
|
sqrt(x) |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
|
x |
|
|
|
Рис. 4. Графики, выведенные на одних координатных осях с размещением легенды |
||||||
Теперь добавим <параметры управления>, управляющие свойствами графиков. Условно они разделены на две группы:
LineSpec — свойства без стандартных имен;
PropertyName — свойства со стандартными именами.
Параметры группы LineSpec определяют тип линии (сплошная, пунктирная и т. д.), цвет линии и вид маркеров (кружок, крестик и т. д.). Значения параметров (они приведены в табл. 4.3 учебного пособия) отображаются символами, которые указываются в апострофах без пробелов в произвольном порядке.
Добавим управляющие параметры группы LineSpec для графиков функций, представленных на рис. 3:
>>figure
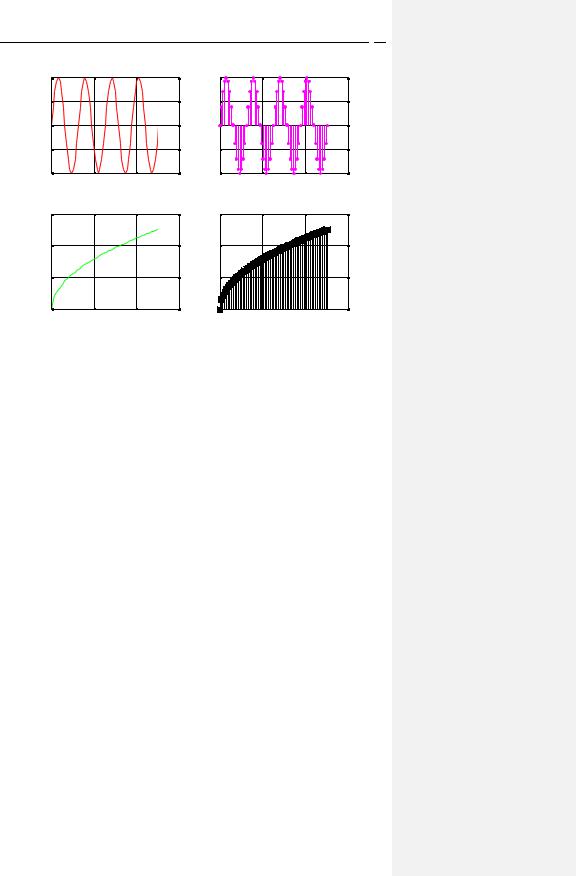
>>subplot(2,2,1), plot(x,y1,'-r'), grid, title('y1(x) = sin(x)')
>>subplot(2,2,2), stem(x,y1,'fill','-m.'), grid, title('y1(x) = sin(x)')
>>subplot(2,2,3), plot(x,y2,'--g'), grid, xlabel ('x')
>>title('y2(x) = sqrt(x)')
>>subplot(2,2,4), stem(x,y2,'fill','-ks'), grid, xlabel ('x')
>>title('y2(x) = sqrt(x)')
Выведенные графики представлены на рис. 5.
12
|
y1(x) = sin(x) |
|
|
y1(x) = sin(x) |
|
||
1 |
|
|
|
1 |
|
|
|
0.5 |
|
|
|
0.5 |
|
|
|
0 |
|
|
|
0 |
|
|
|
-0.5 |
|
|
|
-0.5 |
|
|
|
-1 |
|
|
|
-1 |
|
|
|
0 |
10 |
20 |
30 |
0 |
10 |
20 |
30 |
|
y2(x) = sqrt(x) |
|
|
y2(x) = sqrt(x) |
|
||
6 |
|
|
|
6 |
|
|
|
4 |
|
|
|
4 |
|
|
|
2 |
|
|
|
2 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
10 |
20 |
30 |
0 |
10 |
20 |
30 |
|
|
x |
|
|
|
x |
|
Рис. 5. Графики с добавленными параметрами группы LineSpec
Параметры группы PropertyName имеют следующие стандартные имена:
•LineWidth — толщина линии в пунктах (1 пункт ≈ 0,34 мм); задаются цифрой без апострофов, по умолчанию 0,5;
•MarkerEdgeColor — цвет маркера; задается параметром из табл. 2 в апострофах; по умолчанию совпадает с цветом линий;
•MarkerFaceColor — цвет закрашивания маркера (для замкнутых маркеров); задается параметром из табл. 2 в апострофах; ; по умолчанию совпадает с цветом линий;
•MarkerSize — размер маркера в пунктах; задаются цифрой без апострофов, по умолчанию 7.
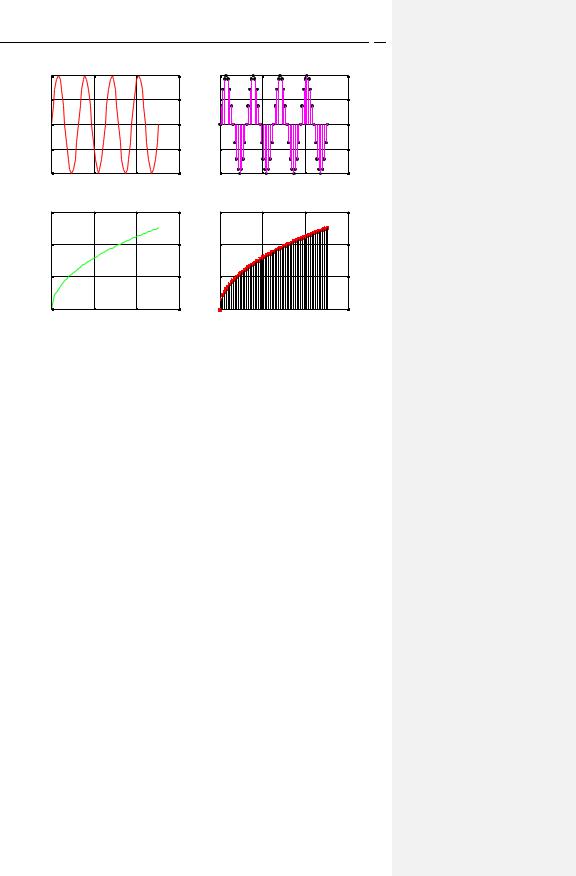
Добавим управляющие параметры группы PropertyName для графиков функций, представленных на рис. 5:
>>figure
>>subplot(2,2,1), plot(x,y1,'-r','LineWidth',2), grid
>>subplot(2,2,2), stem(x,y1,'fill','-m.','MarkerEdgeColor','k'),
grid
>>subplot(2,2,3), plot(x,y2,'--g','LineWidth',2), grid
>>subplot(2,2,4), stem(x,y2,'fill','-ks',...
>>'MarkerEdgeColor','r','MarkerSize',4), grid
Выведенные графики представлены на рис. 6.
13
1 |
|
|
|
1 |
|
|
|
0.5 |
|
|
|
0.5 |
|
|
|
0 |
|
|
|
0 |
|
|
|
-0.5 |
|
|
|
-0.5 |
|
|
|
-1 |
|
|
|
-1 |
|
|
|
0 |
10 |
20 |
30 |
0 |
10 |
20 |
30 |
6 |
|
|
|
6 |
|
|
|
4 |
|
|
|
4 |
|
|
|
2 |
|
|
|
2 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
10 |
20 |
30 |
0 |
10 |
20 |
30 |
Рис. 6. Графики с добавленными параметрами группы PropertyName
Функции plot и stem предназначены для построения графиков в линейном масштабе. На лабораторных работах будут рассмотрены функции с использованием логарифмического масштаба по одной из осей или обеим осям.
В MATLAB представлено большое разнообразие функций для построения специальных графиков. Познакомимся с тремя из них:
1.Функция hist —для построения гистограммы с простейшим форматом: hist(x)
где x — вектор.
Диапазон значений элементов вектора y по умолчанию делится на 10 интервалов, и гистограмма отображает число попаданий значений элементов вектора x в центры данных интервалов.
Цвет столбцов выбирается по умолчанию или с помощью функции:
colormap('<символическое имя палитры>')
которая может ставиться до или после функции построения графика.
Символические имена палитр приведены в табл. 4.5 учебного пособия.
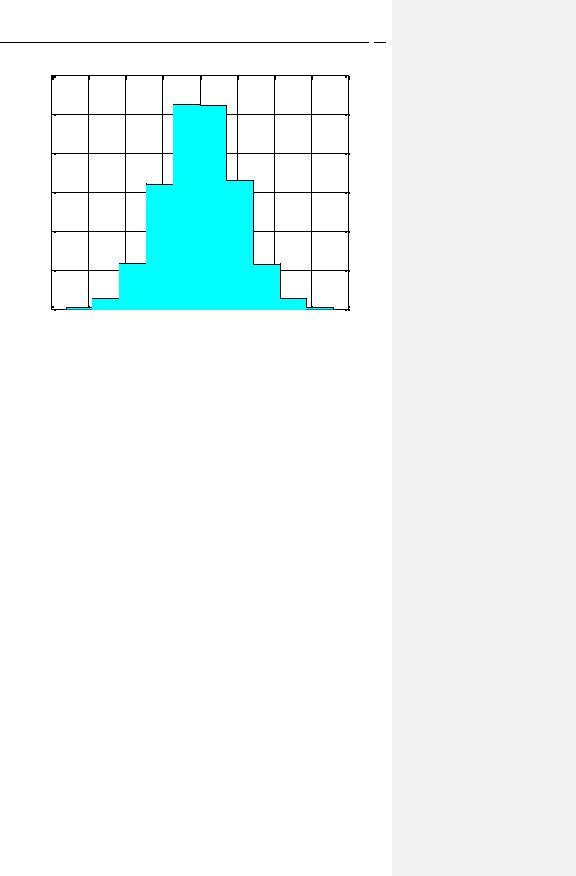
Построим гистограмму нормального белого шума длины 10000 с выбором палитры 'cool' — фиолетово-голубая (рис. 7):
>>figure
>>x = randn(1,10000);
>>hist(x), grid, title('Gaussian White Noise - hist')
>>colormap('cool')
14
Gaussian W hite Noise - hist
3000 |
|
|
|
|
|
|
|
|
2500 |
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
|
|
1500 |
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
Рис. 7. Гистограмма нормального белого шума
2.Функция bar — для построения столбцовой диаграммы с простейшим форматом:
bar(x, width)
где x — вектор; width — ширина столбцов, по умолчанию 0,8, при ширине > 1
Столбцовая диаграмма отображает значения элементов вектора x в виде столбцов, цвет которых выбирается с помощью функции colormap.
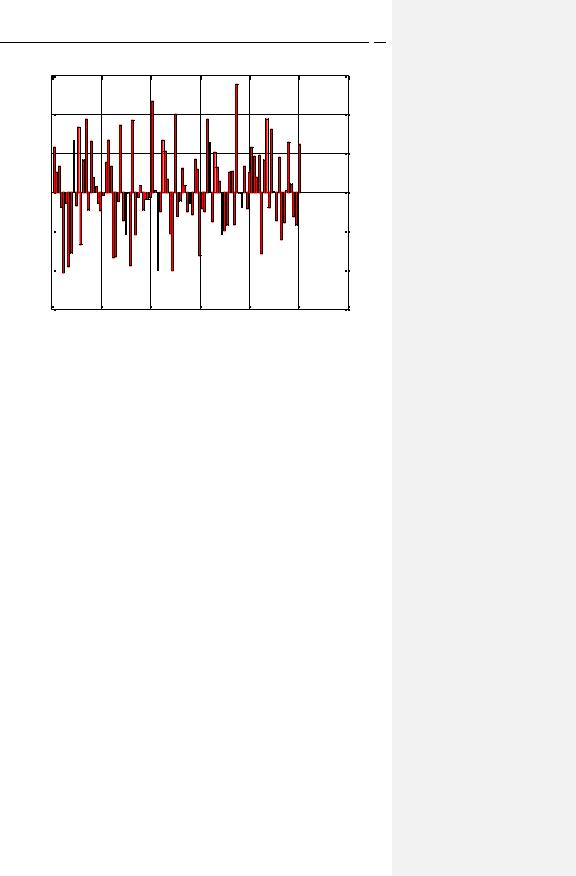
Построим столбцовую диаграмму 100 значений нормального белого шума
(рис. 8):
>>figure
>>x = randn(1,100);
>>bar(x), grid, title('Gaussian White Noise - bar')
>>colormap('flag')
15
Gaussian W hite Noise - bar
3 
2
1
0 |
-1 






-2 




-3 
0 |
20 |
40 |
60 |
80 |
100 |
120 |
Рис. 8. Cтолбцовая диаграмма нормального белого шума
3.Функция pie — для построения круговой диаграммы с простейшим форматом: pie(x,explode)
где x — вектор с положительными значениями элементов; если их сумма > 1, то значения элементов нормируются к их сумме и указываются в процентах; explode — вектор из единиц и нулей, согласованный по длине с вектором x для
"вытаскивания" требуемых фрагментов.
Круговая диаграмма отображает значения элементов вектора x в виде фрагментов круга, цвет которых выбирается с помощью функции colormap.
Построим круговую диаграмму для 8 элементов вектора с "вытаскиванием"
наибольшего и наименьшего элементов (рис. 9):
>>figure
>>x = [0.1 0.8 0.2 0.3 0.4 0.9 0.5 0.6];
>>explode = [1 0 0 0 0 1 0 0];
>>pie(x,explode)
>>colormap('winter')

16
3%
16%
21%
13%
5%
8%
11% |
24% |
|
Рис. 9. Круговая диаграмма 8-элементного вектора
3.10. Трехмерная графика
Трехмерная графика предназначена для построения в трехмерном пространстве графиков функций z(x, y) .
Их построение начинается с формирования сетки на плоскости xOy с помощью функции:
[X,Y] = meshgrid(x,y)
где:
x,y — векторы, формирующие сетки по осям x и y ;
X,Y — матрицы одинакового размера, формирующие сетку на плоскости xOy; количество строк равно длине вектора y, а столбцов — длине вектора x.
Если векторы x и y одинаковы, то допускается короткий формат:
[X,Y] = meshgrid(x)
Средства оформления трехмерных графиков такие же, что и для двумерных (табл. 2), но с учетом дополнительной оси z добавляются функции:
zlabel('<текст>')
zlim([zmin zmax])
В MATLAB представлено большое разнообразие функций для построения трехмерных графиков, с которыми можно познакомиться в справочной системе (разд. 3.9). Для понимания специфики построения трехмерного графика достаточно познакомиться с одной из них, например, с функцией построения графика с сетчатой поверхностью и автоматическим нанесением координатной сетки:
surf (X,Y,Z[,<параметры управления>])
где:
X, Y — матрицы, формирующие сетку на плоскости xOy с помощью функции meshgrid
Z — функция z(x, y) (вектор или матрица);
<параметры управления> — необязательные параметры, управляющие свойствами графика, такие же, как для двумерных графиков.
Палитра цветов графика выбирается с помощью функции colormap.
|
17 |
||
|
|
|
|
Используем функцию surf для построения графика функции |
z = x2 + y 2 на |
||
интервале по осям x и y , равном [−5; 5] , с одинаковыми шагами |
x = y = 0, 25 . |
||
Предварительно сформируем сетку на плоскости xOy с помощью функции meshgrid короткого формата (рис. 10):
>>figure
>>[X,Y] = meshgrid(-5:0.25:5);
>>Z = X.^2+Y.^2;
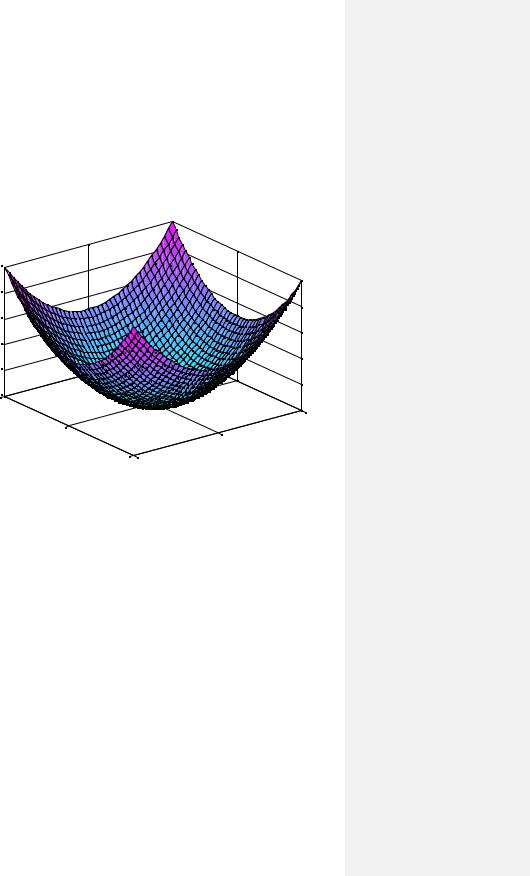
>>surf (X,Y,Z), title('Z = X.^2+Y.^2 - surf')
>>colormap('cool')
Z = X.2+Y .2 - surf
50 
40 
30 
20
10 
0 
5
5
0
0
-5 -5
Рис. 10. Трехмерный график, построенный с помощью функции surf
Рассмотренные ранее <параметры управления> могут использоваться для управления свойствами трехмерных графиков, однако для них предусмотрены и дополнительные средства, в частности:
•команда вывода на поле графика шкалы цветов: colorbar
которая обязательно ставится последней и устанавливает соответствие между значениями функции и их отображением цветом;
•команда преобразования сетчатой поверхности в сплошную: shading interp
Используем эти команды для построения графика той же функции с выводом в отдельные поля текущего графического окна (рис. 11):
>>figure
>>[X,Y] = meshgrid(-5:0.25:5);
>>Z = X.^2+Y.^2;
>>subplot(2,1,1),surf (X,Y,Z), title('colorbar')
>>colormap('cool')
>>colorbar
>>subplot(2,1,2),surf (X,Y,Z), title(' shading interp')
>>shading interp
18
|
colorbar |
|
|
|
|
50 |
|
50 |
|
40 |
|
|
|
30 |
|
|
|
20 |
|
0 |
|
10 |
|
5 |
|
||
0 |
|
5 |
|
0 |
0 |
||
|
|||
|
-5 -5 |
|
|
|
shading interp |
|
|
50 |
|
|
|
0 |
|
|
|
5 |
|
5 |
|
|
0 |
||
|
0 |
||
|
|
||
|
-5 -5 |
|
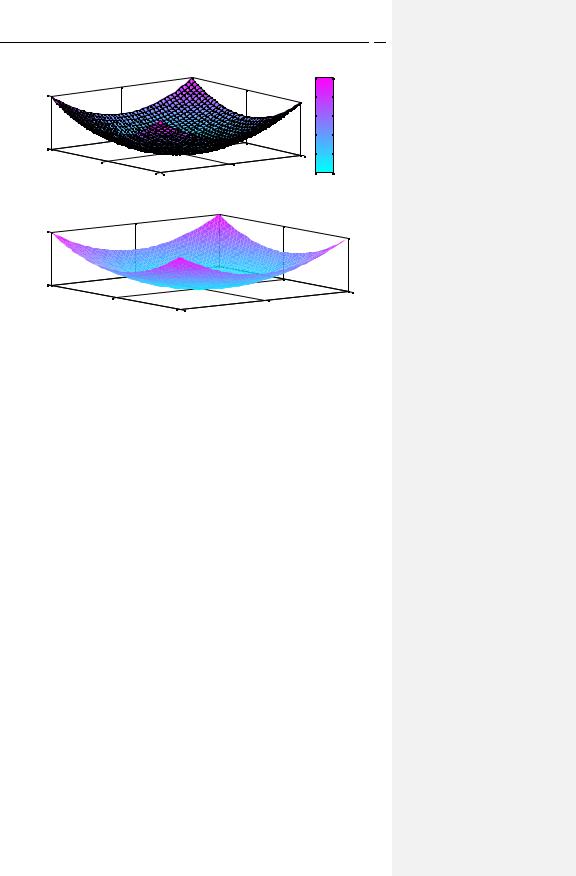
Рис. 11. Трехмерные графики с выводом шкалы цветов (верхний) и преобразованием сетчатой поверхности в сплошную (нижний)
