
MATLAB_03
.pdf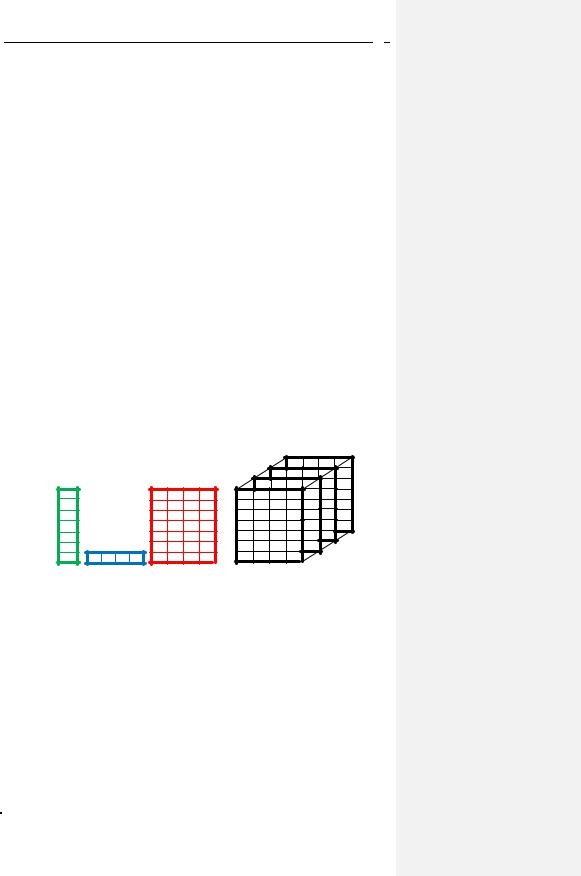
1
Лекция 3. Основные типы массивов и графика в MATLAB
1.Основные типы массивов в MATLAB.
2.Числовые массивы — numeric array.
3.Массивы логического типа — logical array.
4.Массивы символьного типа — char array.
5.Массивы записей (структуры) — struct array.
6.Массивы ячеек — cell array.
7.Определение типа массива.
8.Общие правила при выводе графиков.
9.Двумерная графика.
10.Трехмерная графика.
3.1. Основные типы массивов в MATLAB
Массивом называют упорядоченную совокупность данных, объединенных одним именем.
В линейной алгебре массив характеризуется:
размерностью.
Размерность массива равна количеству индексов k, которые указывают на упорядоченность данных в k-мерном пространстве.
Если данные упорядочены в строку (столбец), то их порядок следования указывается с помощью одного индекса — одномерный массив (вектор).
Если данные упорядочены одновременно по строкам и по столбцам, то их порядок следования указывается с помощью двух индексов — двумерный массив
(матрица)
Если данные упорядочены по матрицам, то их порядок следования указывается с помощью трех индексов — трехмерный массив и т. д.
Рис. 1. Графическое отображение одномерного, двумерного и трехмерного массивов
размером.
Размер массива указывают в виде произведения числа элементов по каждому индексу: n — одномерный массив; m × n — двумерный; m × n × l — трехмерный и т. д.
типом.
Тип массива определяется типом его элементов.
В MATLAB тип массива не инициализируется (предварительно не объявляется).
Все массивы в MATLAB можно объединить в две группы:
числовые массивы;
нечисловые массивы.
В табл. 1 представлены их основные типы массивов из этих групп.
Таблица 1. Основные типы массивов в MATLAB
Числовые массивы (numeric array) |
Нечисловые массивы |
|
|

2
Тип массива |
Наименование |
Тип массива |
наименование |
|
|
|
|
double |
вещественный, |
logical array |
логический |
|
двойной точности |
|
|
|
|
|
|
single |
вещественный, |
char array |
массив символов |
|
одинарной точности |
|
|
|
|
|
|
int<…> |
целый со знаком, |
struct array |
массив записей |
<…> — 8,16,32,64 |
8, 16, 32,или 64- |
(structure) |
(структура) |
|
битовый |
|
|
|
|
|
|
uint<…> |
целый без знака, |
cell array |
массив ячеек |
|
8, 16, 32, или 64- |
|
|
|
битовый |
|
|
|
|
|
|
Напомним, что в MATLAB по умолчанию любая переменная считается матрицей, поэтому далее особое внимание уделено матрицам различных типов.
Исключение составляет массив записей — особый тип нечислового массива, не адекватный его определению в линейной алгебре.
3.2. Числовые массивы — numeric array
Числовые массивы объединяют в себе следующие типы массивов (табл. 1):
•double;
•single;
•int8, int16, int32, или int64;
•uint8, uint16, uint32, или uint64.
По умолчанию матрица относится к типу double.
Элементами матриц типа double являются константы вещественного типа двойной точности (15 значащих цифр после запятой).
Это значит, что во всех внутренних вычислениях элементы матриц воспринимаются как вещественные числа двойной точности.
В Лекции 2 по умолчанию рассматривались матрицы типа double.
Элементами матриц типа single являются константы вещественного типа одинарной точности (вдвое меньшей).
Преобразование матрицы A типа double в матрицу типа single выполняется с помощью функции:
single(A)
С этим типом матриц мы работать не будем.
Элементами матриц типа int8, int16, int32, и int64 являются константы целого
типа со знаком.
Для элементов матриц типа int8 целые константы расположены в диапазоне от –128
до 127, где 128 = 27 и т. д.
Во внутренних вычислениях им соответствуют двоичные эквиваленты,
соответственно, длиной 8, 16, 32 или 64 бита, где старший бит — знаковый.
Элементами матриц типа uint8, uint16, uint32, и uint64 являются константы
целого типа без знака.
Для элементов матриц типа uint8 целые константы расположены в диапазоне от 0
до 255, где 255 = 28 и т. д.
Во внутренних вычислениях им соответствуют двоичные эквиваленты,
соответственно, длиной 8, 16, 32 или 64 бита, где старший бит — значащий.
Матрицы типа int8 и uint8 (и им подобные) вводятся с помощью функций:
int8(A)
uint8(A)
где A — матрица с элементами в квадратных скобках:
Например:

3
>> A = int8([120 -115;-75.7 14.1])
A=
120 -115 -76 14
Преобразование матрицы A типа double в матрицы типа int8 и uint8 (и им подобные) выполняется с помощью тех же функций:
Например, сформируем A типа double:
>> A = [-15.7 129.5;-130.8 13.9]
A=
-15.7000 129.5000
-130.8000 13.9000
Преобразуем ее в матрицу B типа int8:
>> B = int8(A)
B=
-16 127
-128 14
и в матрицу C типа uint8:
>> C = uint8(A)
C =
0130
014
Сматрицами типа int и uint разрешены операции:
• |
поэлементные арифметические; |
• матричного сложения и вычитания; |
|
• |
отношения; |
• |
логические. |
С матрицами типа uint дополнительно разрешены побитовые операции:
С матрицами типа int и uint запрещены операции:
• матричного умножения, деления и возведения в степень;
• вычисления большинства элементарных функций.
3.3. Массивы логического типа — logical array
Массив логического типа — это нечисловой массив (табл. 1), элементами которого являются логические константы 1 (true) и 0 (false).
Элементы логической матрицы могут вводиться как true и false или 1 и 0, но выводятся только как 1 и 0:
>> A = [true false;false true]
A =
10
01
>>B = [0 1;1 1]
B = |
|
0 |
1 |
1 |
1 |
В MATLAB тип массива не инициализируется, поэтому во внутренних вычислениях матрица с элементами 1 и 0 может быть отнесена как к типу double, так и к логическому типу, в зависимости от выполняемых операций.
С матрицами логического типа допустимы операции отношения и логические операции:
>> A > B % операция отношения

4
ans =
10
00
>>A | B % логическая операция ИЛИ
ans =
11
11
>>A+B % арифметическая операция
ans =
11
12
Элементы матриц логического типа могут задаваться в виде логических выражений:
>> x = [sin(3)<0.5 1;0 (sin(3)<0.1)&(cos(3)<0.2)]
x =
11
00
3.4.Массивы символьного типа — char array
Массив символьного типа — это нечисловой массив (табл. 1), элементами которого являются символьные константы — любые последовательности символов, заключенные в апострофы.
Матрица символьного типа формируется по столбцам:
•элементы столбца должны содержать одинаковое число символов, при этом пробел считается равнозначным символом.
Автоматическое добавление пробелов в элементах столбца с выравниванием по левому краю выполняется с помощью функции:
a = char('<char1>','<char2>'...)
где <char1>,<char2>... — элементы столбца — символьные константы с произвольным количеством символов:
>>a = char('Newton','Scientist','English') a =
Newton Scientist English
элементы строки представляют собой слитную запись:
>>b = ['Newton' 'Scientist' 'English']
a =
NewtonScientistEnglish
Пробелы должен предусмотреть пользователь:
>>b = [' Newton ' ' Scientist ' ' English'] a =
Newton Scientist English
элементы матрицы представляют собой столбцы, сформированные с помощью функций char с соответствующими строками.
Одна функция char описывает один столбец матрицы.
Для выравнивания столбцов необходимо добавить пробелы:
>>X = [char('a','aaa') char(' bb',' b') char(' ccc',' c')]
X =
abb ccc
aaab c
Внекоторых приложениях необходимо представить матрицу числового типа в виде матрицы символьного типа. Такое преобразование выполняется с помощью функции:
num2str(A)
Например:

5
>> A = [-15.7 129.5;-130.8 13.9]
A=
-15.7000 129.5000
-130.8000 13.9000
>> simbol_A = num2str(A)
simbol_A =
-15.7 |
129.5 |
-130.8 |
13.9 |
>> B = int8(A) |
|
B = |
|
-16 |
127 |
-128 |
14 |
>> simbol_B = num2str(B)
simbol_B =
-16 127
-128 14
Однако обратное преобразование невозможно!
3.5. Массивы записей (структуры) — struct array
Массив записей (структура) — это нечисловой массив (табл. 1), элементами которого являются записи.
Массив записей используется в различных приложениях для описания
M объектов, i = 1, 2, ... , M ,
каждый из которых характеризуется
N параметрами, n = 1, 2, ... , N .
Массив записей (структура) упорядочивает записи об объектах и их параметрах.
Это особый тип массива, не адекватный его определению в линейной алгебре. Прежде чем дать ему более строгое определение, познакомимся с новыми терминами:
1.поле (field) — имя n-го параметра: скаляра, вектора или матрицы заданного типа;
Число полей равно числу параметров N .
2.значение поля — значение n-го параметра;
3.список полей — список имен параметров;
4.запись — список полей, одинаковый для всех объектов;
Число записей равно числу объектов M .
5.значение записи — список полей с их значениями для i -го объекта.
Массив записей (структура) представляет собой упорядоченную совокупность значений записей, объединенная одним именем с одним индексом.
Значение i -й записи формируется по каждому n-му полю:
<имя массива>(<i>).<имя n-го поля> = <значение n-го поля>
Имя массива записей выбирается так же, как обычно для любой переменной.
Размер массива записей равен числу записей M .
Для формирования M записей по N полям потребуется M × N операторов присваивания.
Сформируем массив записей (структуру) с именем personal для описания трех объектов — трех известных ученых — четырьмя параметрами:
M = 3 , i = 1, 2, 3 ;
N = 4 , n = 1, 2, 3, 4 .
6
Запись будет включать в себя список из N = 4 полей — имен параметров: surname — фамилия ученого — скаляр символьного типа;
data — дата рождения ученого (число, месяц, год) — вектор численного типа; area — область науки — скаляр символьного типа;
disciples — наличие известных учеников — скаляр логического типа.
Для формирования M = 3 записей по N = 4 полям потребуется операторов присваивания:
>>personal(1).surname = 'Newton';
>>personal(2).surname = 'Darvin';
>>personal(3).surname = 'Fourier';
>>personal(1).data = [25 12 1642];
>>personal(2).data = [12 2 1809];
>>personal(3).data = [21 3 1768];
>>personal(1).area = 'физика';
>>personal(2). area = 'биология';
>>personal(3).area = 'математика';
>>personal(1).disciples = false;
>>personal(2).disciples = false;
>>personal(3).disciples = true;
Размер матрицы записей personal равен числу записей M = 3 .
Список полей выводится по имени массива записей:
>> personal personal =
1x3 struct array with fields: surname
data area disciples
Значение i-й записи выводится по имени массива записей с указанием индекса в круглых скобках. Например, значение 2-й записи:
>> personal(2) ans =
surname: 'Darvin' data: [12 2 1809]
area : ' биология' disciples: 0
Значение поля в i-й записи выводится по имени массива записей с указанием индекса в круглых скобках и, после точки, имени поля. Например, значение поля surname первой записи:
>> personal(1).surname |
|
ans = |
|
Newton |
Отформатировано: русский |
|
Значения поля во всех записях выводятся по имени массива с указанием имени поля после точки. Например, значения поля surname:
>> personal.surname ans =
Newton ans = Darvin ans = Fourier
3.6. Массивы ячеек — cell array
Массив ячеек — это самый сложный нечисловой массив (табл. 1), элементами которого являются ячейки — массивы любой размерности, любого размера и типа.
Подобно матрице в линейной алгебре, матрица ячеек имеет строки и столбцы, и ее размер равен их произведению m × n.
Матрицу ячеек можно формировать по-разному. Например, сначала сформировать ее элементы, а затем ввести их подобно матрице типа double, но с элементами в
фигурных скобках.
Сформируем матрицу ячеек A размером 2×3. Сначала сформируем ее элементы:
7
>> A1 = |
[1 2 3 4;5 6 7 8]; |
% матрица типа double |
|
>> A2 = |
[true false true]; |
% вектор типа logical |
|
>> A3 |
= |
eps; |
% скаляр типа double |
>> A4 |
= |
personal; |
% массив записей |
>> A5 |
= |
[char('a','aaa') char(' bb',' b')]; |
% матрица символов |
>> A6 |
= |
int8([159.7 -115.7;-75.7 14.1]); |
% матрица типа int8 |
а затем из них сформируем матрицу ячеек A:
>> A = {A1 A2 A3;A4 |
A5 A6} |
|
|
A = |
|
|
|
[2x4 double] |
[1x3 |
logical] |
[2.2204e-016] |
[1x3 struct] |
[2x6 |
char ] |
[2x2 int8] |
Другие способы формирования матрицы ячеек рассматриваются на лабораторных занятиях.
Вывод элементов массива ячеек выполняется по его имени с указанием индексов в
фигурных скобках:
>> A{1,2} ans =
1 0 1
>> A{2,1} ans =
1x3 struct array with fields: surname
data area disciples
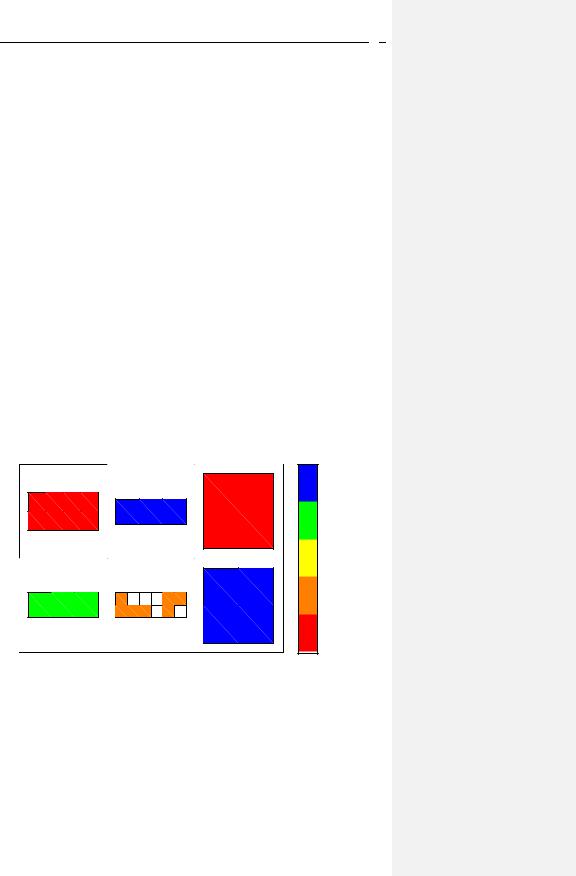
Для наглядного представления матрицы ячеек предусмотрен ее графический вывод с |
помощью функции: |
cellplot(A,'legend') |
Рис. 2. Графическое представление матрицы ячеек |
3.7. Определение типа массива
Для определения типа массива служит функция
class(<имя переменной>)
Например, для рассмотренных выше переменных A2, A5 и A:
>> class(A2),class(A5),class(A)
ans =
logical

8
ans =
char
ans =
cell
Кроме того, для определения типа массива можно воспользоваться функциями,
возвращающими 1 (true), если аргумент, в круглых скобках соответствует объявленному типу, и 0 (false) — в противном случае. Имена этих функций начинаются с приставки "is …", что переводится как вопрос "является ли?":
isnumeric(<имя переменной>)
islogical(<имя переменной>) ischar(<имя переменной>)
isstruct(<имя переменной>) iscell(<имя переменной>)
Например, для рассмотренных выше переменных A5 и A:
>>isnumeric(A5) ans =
0
>>iscell(A)
ans =
1
3.8. Общие правила при выводе графиков
Огромное разнообразие графических средств системы MATLAB является одним из ее основных преимуществ перед другими пакетами программ (Лекция 1).
Прежде чем перейти собственно к построению графиков, познакомимся общими правилами при их выводе:
Текущий график выводится в текущее графическое окно Figure со стандартным меню и панелью инструментов.
Первый график выводится в окно Figure 1, а каждый следующий — в то же окно
с автоматическим удалением предыдущего графика.
Вывод графиков в отдельных графических окнах Figure 1, Figure 2, ... ,
выполняется с помощью функции:
figure
которая ставится перед выводом каждого следующего графика.
Присваивание имени текущему графическому окну Figure выполняется с помощью функции:
figure('Name','<Имя графика>','NumberTitle','off')
Вывод нескольких графиков на одних координатных осях в текущее графическое окно Figure выполняется по команде:
hold on
которая ставится перед выводом каждого следующего графика.
Удаление всех графиков из текущего графического окна Figure выполняется по команде:
hold off

9
которая ставится перед выводом нового графика (графиков) в данное окно.
Вывод нескольких независимых графиков в текущее графическое окно Figure
выполняется путем его разбиения на отдельные поля с помощью функции: subplot(m,n,p)
где m × n — размер матрицы графического окна: m строк и n столбцов; p —
порядковый номер поля выводимого графика, считая по строкам слева направо.
3.9. Двумерная графика
Для построения графиков используются специальные функции, полная информация о которых дается в справочной системе MATLAB. После обращения к ней по команде главного меню Help | Product Help следует выбрать раздел MATLAB и в нем — раздел Graphics.
Двумерная графика предназначена для построения графиков в двумерном пространстве (на плоскости).
Начнем знакомство с двух "классических" функций построения графиков в декартовой системе координат:
1.Функция plot — для графиков функций y(x) , заданных в дискретных точках, с
линейной интерполяцией между соседними значениями: plot(x,y[,<параметры управления>])
где:
x, y — аргумент и функция y(x) (векторы или матрицы), согласованные по длине или размеру.
Если x, y — матрицы, то построение графиков выполняется по столбцам.
В отсутствие аргумента x аргументами служат индексы элементов вектора или столбцов матрицы.
<параметры управления> — необязательные параметры (признак необязательности — квадратные скобки), управляющие свойствами графиков, которые рассматриваются далее.
y(x)
Функцию plot можно использовать для построения графиков нескольких функций y1(x1 ) , y2 (x2 ) , …:
plot(x1,y1[,<параметры управления>],x2,y2[,<параметры управления>]...)
2.Функция stem — для графиков функций y(x) , заданных в дискретных точках, с
выводом значений в виде отсчетов с маркерами: stem(x,y[,'fill'] [,<параметры управления>])
Необязательный параметр 'fill' указывает на закрашивание маркеров.
Функцию stem используют для построения графиков последовательности чисел, которую коротко называют " последовательностью".
Прежде чем привести примеры построения графиков, познакомимся с общими правилами их оформления (табл.2).
|
Таблица 2. Функции оформления графиков |
|
|
Функция |
Назначение |
|
|
grid |
Нанесение координатной сетки |
|
|
title('<текст>') |
Заголовок графика |
|
|
xlabel('<текст>') |
Обозначение осей x, y |
10
ylabel('<текст>')
xlim([xmin xmax]) |
Установка границ по осям x, y |
ylim([ymin ymax])
legend('legend1','legend2',...) Размещение легенды в порядке вывода графиков
Отметим, что в приведенных функциях не всегда воспринимается <текст> с русским алфавитом, поэтому рекомендуется использовать латинский алфавит.
Используем функции plot и stem для построения графиков функций y = sin(x) и y =  x на интервале x [0; 8π] с шагом x = π
x на интервале x [0; 8π] с шагом x = π 8 . Выведем графики в отдельные поля текущего графического окна с помощью функции subplot. Функция построения графика ставится после функции subplot через запятую, а функции оформления — после функции построения графика через запятую или на отдельной строке:
8 . Выведем графики в отдельные поля текущего графического окна с помощью функции subplot. Функция построения графика ставится после функции subplot через запятую, а функции оформления — после функции построения графика через запятую или на отдельной строке:
>>x = 0:pi/8:8*pi;
>>y1 = sin(x); y2 = sqrt(x);
>>subplot(2,2,1), plot(x,y1), grid, ylabel('y1(x)')
>>title('y1(x) = sin(x) - plot')
>>subplot(2,2,2), stem(x,y1,'fill'), grid, ylabel('y1(x)')
>>title('y1(x) = sin(x) - stem')
>>subplot(2,2,3), plot(x,y2), grid, xlabel ('x'), ylabel('y2(x)')
>>title('y2(x) = sqrt(x) - plot')
>>subplot(2,2,4), stem(x,y2,'fill'), grid, xlabel ('x')
>>ylabel('y2(x)'), title('y2(x) = sqrt(x) - stem')
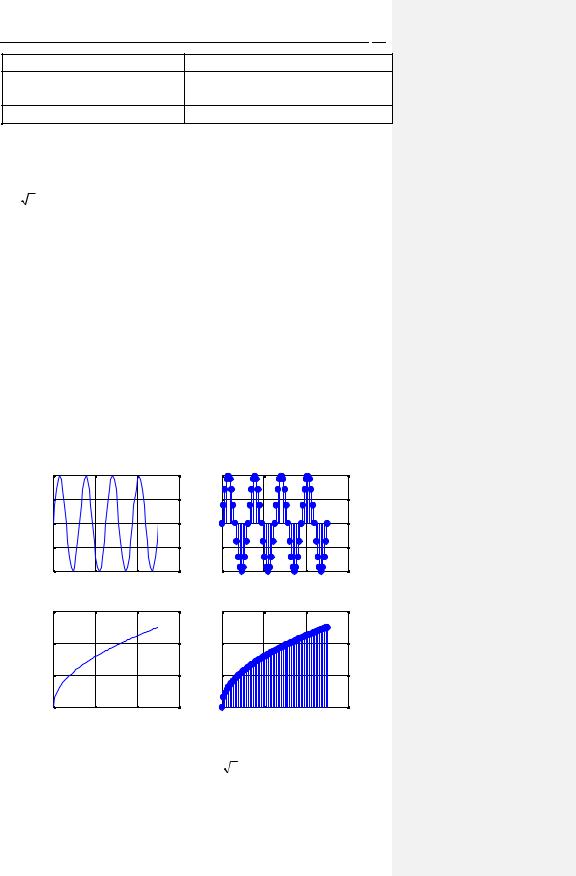
Выведенные графики представлены на рис. 3. |
|
|
|
||||||
|
|
y1(x) = sin(x) - plot |
|
|
|
y1(x) = sin(x) - stem |
|
||
|
1 |
|
|
|
|
1 |
|
|
|
|
0.5 |
|
|
|
|
0.5 |
|
|
|
) |
|
|
|
|
) |
|
|
|
|
y 1(x |
0 |
|
|
|
y 1(x |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
-0.5 |
|
|
|
|
-0.5 |
|
|
|
|
-1 |
|
|
|
|
-1 |
|
|
|
|
0 |
10 |
20 |
30 |
|
0 |
10 |
20 |
30 |
|
|
y2(x) = sqrt(x) - plot |
|
|
|
y2(x) = sqrt(x) - stem |
|
||
|
6 |
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
y 2(x ) |
|
|
|
|
y 2(x ) |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
10 |
20 |
30 |
|
0 |
10 |
20 |
30 |
|
|
|
x |
|
|
|
|
x |
|
Рис. 3. Графики, построенные с помощью функций plot и stem
Построим графики функций y = sin(x) и y =  x с помощью функции plot и
x с помощью функции plot и
выведем их на одних координатных осях с размещением легенды (рис. 4):
>> figure
