ГОСы / Трактора и Автомобили / 16

16. Трансмиссии современных автомоби­лей и тракторов состоят из отдельных механизмов, которые могут крепиться к раме машины жестко или через упру­гую подвеску. Оси соединяемых валов этих агрегатов часто располагаются в разных плоскостях и под углом одна к другой.

Для компенсации несоосностей валов, возникших в результате деформаций рамы или монтажных неточностей (в пре­делах 5°), соединения неподрессореиных агрегатов с подрессоренными, а также для привода ведущих управляемых ко­лес автомобилей (в пределах до 40°) при­меняются различного типа карданные передачи. В такую передачу входят три основных элемента: карданные шар­ниры или карданные муфты, валы и опо­ры.

Работа карданной передачи, имеющей переменные углы, сопровождается изме­нением расстояния между механизмами. Это должно учитываться в конструкции передачи (применение подвижных шлицевых соединений).

Требования к карданным передачам зависят от их назначения. Но все пере­дачи должны обеспечивать равномерную синхронную передачу энергии между соединяемыми агрегатами; обладать вы­соким КПД; работать бесшумно. Сбо­рочные единицы и детали карданных пе­редач должны быть унифицированы.

По числу применяемых шарниров пе­редачи могут быть одно-, двух-, трехшарнирными и т. д. На автомобилях и тракторах наиболее распространена двухшарнирная передача. Если механизмы установлены рядом на одном основании, то применяют одношарнирную передачу.

Карданный шарнир — основной эле­мент карданной передачи. Его тип опре­деляет кинематику передачи, макси­мально допустимые углы наклона ва­лов, влияет на частоты крутильных ко­лебаний в трансмиссии. Долговечность карданной передачи определяется сроком службы шарниров.

По кинематике карданные шарниры делятся на шарниры равных и неравных угловых скоростей (синхронные и асин­хронные).

Синхронные шарниры применяются в приводах ведущих управляемых колес автомобилей. На тракторах используют­ся асинхронные шарниры.

Из карданных муфт в автотракторо­строении применяют жесткую зубчатую и упругую с диском или резинометаллическими втулками.

Карданные муфты применяют в пере­дачах с небольшим углом наклона между валами (3...5°). Они бывают жесткие и упругие.

В жестких муфтах наклон валов обес­печивается за счет зазоров между дета­лями, а в упругой — за счет деформации упругого элемента муфты.

Составить уравнение тягового баланса.

Силы сопротивления движению

Наряду с толкающей силой Х_к на движущиеся прямолинейно трактор и автомобиль действуют в продольной плоскости силы сопротивления движению. Рассмотрим, каковы эти силы в самом общем случае, когда движение носит неустановившийся характер, дорога имеет наклон к горизонту и к прицепному крюку машины приложено тяговое сопротивление. На рисунке 1 показан автомобиль, движущийся в указанных условиях, и нанесены действующие на него в продольной плоскости силы: движущие и сопротивляющиеся движению. Автомобиль имеет задние ведущие и передние направляющие колеса, радиусы которых равны силовому (динамическому) радиусу r_к, имеющему у всех колес - задних и передних - одинаковое значение. Принято, что движение происходит ускоренно и что угол подъема, преодолеваемого автомобилем, равен .

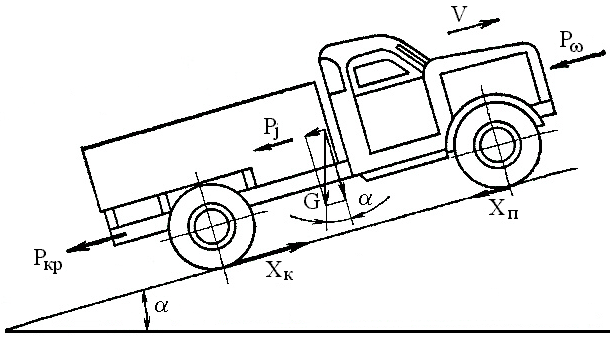
Рисунок 4 - Схема сил движущих и сил сопротивляющихся движению, действующих на автомобиль в продольной плоскости.

На схеме нанесены следующие силы:

Х_к – толкающая сила задних колес, являющаяся движущей силой;

Х_п – реакция, возникающая между дорогой и передними колесами под действием толкающего усилия, приложенного к передним колесам со стороны остова автомобиля; реакция Х_п параллельна поверхности пути и направлена против движения;

G - вес автомобиля;

Р_j - сила инерции, возникающая вследствие неравномерной скорости прямолинейно-поступательного движения автомобиля (моменты касательных сил инерции вращающихся масс учитываются при определении сил Х_к и Х_п); в рассматриваемом случае ускоренного движения сила инерции Р_j препятствует движению;

P_ - сопротивление воздуха

Р_кр - тяговое сопротивление, создаваемое прицепом.

Воспользуемся схемой сил, приведенной на рисунке 1, и напишем уравнение проекций на поверхность пути сил, движущих автомобиль, и сил, препятствующих движению. Получим уравнение, выражающее тяговый баланс автомобиля: