Кромпьютерный лабораторный практикум

21

Лабораторная работа № 3-06к

ВНЕШНИЙ ФОТОЭФФЕКТ

Компьютерная модель «Фотоэффект» в сборнике компьютерных моделей «Открытая физика»

раздел «Квантовая физика»

Цель работы

На компьютерной модели внешнего фотоэффекта подтверждение закономерностей внешнего фотоэффекта; определение красной границы фотоэффекта, работы выхода электронов из фотокатода и постоянной Планка.

Методика виртуального эксперимента

В данной работе используется компьютерная модель, основанная на методе изучения закономерностей внешнего фотоэффекта на установке, в которой два электрода

(катод К из исследуемого металла и анод А) в вакуумной трубке подключены к батарее так, что с помощью потенциометра можно изменять значение и знак подаваемого на электроды напряжения, величина которого измеряется вольтметром (V). Ток,

возникающий в электрической цепи при освещении катода монохроматическим светом

(через кварцевое окошко), измеряется включенным в цепь амперметром (А). Этот ток называют фототоком.

Сила фототока I прямо пропорциональна числу фотоэлектронов N, долетающих

до анода за единицу времени

где N - число фотоэлектронов, достигших анода за время t, е - заряд электрона.

22

По теории Эйнштейна, каждый квант падающего света поглощается только

одним электроном, поэтому число вырванных фотоэлектронов должно быть

пропорционально интенсивности света. Согласно закону сохранения энергии,

уравнение Эйнштейна для внешнего фотоэффекта

где hν - энергия падающего на металл фотона, Авых - работа выхода электрона из

фотоэлектронов.

Минимальная частота νкр (или максимальная длина волны λкр), при которой еще

наблюдается фотоэффект, т.е. для которой энергия падающего на катод фотона равна работе выхода,

называется красной границей фотоэффекта.

Запирающим (или задерживающим) напряжением называется минимальное тормозящее напряжение между анодом вакуумной лампы (фотоэлемента) и

фотокатодом, при котором отсутствует ток в цепи этой лампы, т.е. фотоэлектроны не долетают до анода. При таком напряжении кинетическая энергия электронов у катода

равна потенциальной энергии электронов у анода, откуда следует выражение:

Откройте компьютерную модель «Фотоэффект». Внимательно рассмотрите

модель, найдите все регуляторы и другие элементы. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ ещё раз).

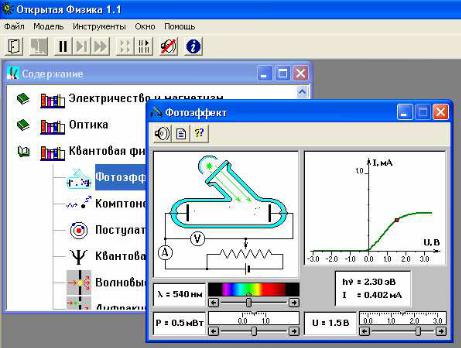
23

Рис. 45. Окно компьютерной модели «Фотоэффект».

В компьютерной модели можно с помощью движков менять длину волны λ падающего на фотокатод света, мощность падающего света (иначе говоря, интенсивность света), величину и знак напряжения U электростатического поля между электродами вакуумной лампы. Компьютерная модель фиксирует численные значения энергии фотона

(hν), падающего на фотокатод, и величину фототока I.

Установив маркером мыши любое значение длины волны падающего на фотокатод света, понаблюдайте процессы движения электронов при разных значениях мощности излучения. Затем проделайте те же наблюдения при определенной мощности для разных длин волн.

Зацепите мышью движок реостата регулятора интенсивности (мощности)

облучения фотокатода и установите его на максимум. Аналогичным образом установите нулевое напряжение между анодом и фотокатодом и минимальную длину волны падающего на фотокатод света. Наблюдайте движение электронов в фотоэлементе,

изменяя напряжение до запирания фототока ( показания тока I = 0).

24

Порядок выполнения работы

1.Запустите, дважды щелкнув мышью, виртуальный эксперимент

«Фотоэффект».

2. Установите нулевое напряжение между анодом и фотокатодом. Зацепив мышью, перемещайте метку на спектре, постепенно увеличивая длину волны падающего на фотокатод света λ. Добейтесь полного отсутствия фототока (показания тока I = 0).

Зафиксируйте (перемещая щелчками по стрелке движка) самую большую длину волны

(она будет равна λкр), при которой фототок еще присутствует. Запишите в тетрадь

значение длины волны красной границы фотоэффекта (λкр).

таблицы 1 для вашего варианта (в которой i - это номер измерения).

5.Перемещая мышью метку на спектре, установите такое максимальное значение длины волны λ = λ1, при котором прекращается фототок (при визуальном наблюдении движения электронов вы видите, что электроны не долетают до анода, а

движутся обратно к катоду), при это амперметр показывает ток I = 0.

6.Значения λ1 и Uзап1 занесите в таблицу 2.

7.Повторите измерения (пункты 3 – 6) для трех других значений Uзап из таблицы 1 для вашего варианта.

Таблица 1.

Значения запирающего напряжения (не перерисовывать).

25

Обработка результатов измерений

1.Вычислите численное значение работы выхода материала фотокатода,

используя формулу (3) и экспериментально установленную длину волны красной границы фотоэффекта. Используя таблицу 3, определите из какого материала изготовлен катод вакуумной лампы (обратите внимание на размерность работы выхода в таблице).

2.Вычислите и запишите в таблицу 2 обратные длины волн.

3.Постройте график зависимости модуля напряжения запирания (Uзап) от

4.Определите численное значение постоянной Планка, используя график и

аргумента.

5.Запишите ответы и проанализируйте ответы и график.

Таблица 3

Значения работы выхода для некоторых материалов

26

Библиографический список

Основной

Савельев И. В. Курс общей физики: В 5 кн. М: АСТ: Астрель, 2006. Кн. 5.

Капуткин Д.Е., Шустиков А.Г. Физика. Обработка результатов измерений при

выполнении лабораторных работ. (№ 805). М.: МИСиС. «Учеба». 2007.

Дополнительный

Сивухин Д.В. Общий курс физики. Т.5. М.: Физматлит, 2002.

Контрольные вопросы

1.Что такое фотон? Напишите формулу вычисления энергии фотона.

2.Что называют внешним фотоэффектом? Перечислите условия, при которых возможен внешний фотоэффект. Напишите уравнение Эйнштейна для внешнего фотоэффекта и поясните физический смысл входящих в него величин. Что называют работой выхода и красной границей фотоэффекта?

3.Объясните принцип действия электрической схемы наблюдения внешнего фотоэффекта в данной работе. Нарисуйте и поясните вольт - амперную характеристику вакуумного фотоэлемента. Отличаются ли вольт – амперные характеристики различных материалов? ( Ответ поясните).

4.Дайте определение фототока. От чего зависит величина фототока?

5.Поясните физический смысл запирающего (задерживающего) напряжения.

Изменится ли величина запирающего напряжения, если: а) не меняя источник

монохроматического излучения, изменить материал фотоэлемента? б) не меняя материал

фотоэлемента, изменять монохроматическое излучение?

6.Задача. Найти длину волны λ света, вырывающего из металла электроны,

которые полностью задерживаются разностью потенциалов U = 3 В. Фотоэффект

начинается при частоте света ν 0 = 6 1014 Гц. Найти работу выхода электрона из этого

металла.

27

Лабораторная работа № 3-07к

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА ПО СПЕКТРУ

ИЗЛУЧЕНИЯ АТОМАРНОГО ВОДОРОДА

Компьютерная модель «Постулаты Бора» в сборнике компьютерных моделей «Открытая физика»

раздел «Квантовая физика»

Цель работы

Знакомство с планетарной и квантовой моделями атома при моделировании процесса испускания и поглощения электромагнитного излучения атомом водорода;

подтверждение закономерностей формирования линейчатого спектра излучения атомарного водорода и определение постоянной Ридберга.

Методика виртуального эксперимента

В данной работе используется компьютерная модель, основанная на постулатах

Бора.

∙Первый постулат Бора: в атоме существуют стационарные (не изменяющиеся во времени) состояния, характеризующиеся определёнными значениями энергии, в

которых он не излучает энергии.

∙Второй постулат Бора: при переходе электрона с одной орбиты на другую излучается или поглощается один фотон с энергией hν, равной разности энергий

соответствующих стационарных состояний:

28

где En и Em– соответственно энергии стационарных состоянии атома до (En) и после (Em)

излучения или поглощения.

Набор возможных дискретных частот (2) квантовых переходов определяет линейчатый

спектр атома

Связь длины волны λ с её частотой ν определяется формулой

где с – скорость света в вакууме.

Спектры излучения и поглощения атомов состоят из отдельных спектральных

линий. Экспериментально установлено, что спектр излучения атома водорода состоит из серии линий, длины волн которых вычисляются по обобщенной формуле Бальмера:

где λ – длина волны спектральной линии в спектре атома водорода; R – постоянная

номер уровня, с которого переходит электрон (ni). Фиксированное число n0 определяет

серию, число ni определяет отдельные линии соответствующей серии и принимает значения для этой серии ni = n0 +1, n0 +2, n0 +3 и т.д..

Спектральной серией называется совокупность линий излучения,

соответствующих переходу электрона в атоме водорода на один и тот же нижний

уровень энергии:

29

В компьютерной модели номер энергетического уровня в атоме водорода обозначен как орбита; например, для первого энергетического уровня n = 1 это будет орбита 1.

Откройте компьютерную модель «Постулаты Бора». Внимательно рассмотрите модель, найдите все регуляторы и другие элементы виртуального эксперимента. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ ещё раз). Подводя маркер к любому уровню энергии электрона в окне модели и нажимая левую кнопку мыши, понаблюдайте за происходящим в окне модели: при каких переходах электрона атом излучает энергию (свет) и когда поглощает? Зарисуйте необходимое в свой конспект лабораторной работы

В данной модели можно устанавливать номер орбиты от 1 по 6. Компьютерная модель фиксирует энергетические переходы электрона в атоме: направленная вверх стрелочка характеризует поглощение энергии атомом, а разница численных значение энергии – это энергия поглощенного при этом кванта света; направленная вниз стрелочка характеризует излучение энергии атомом, а разница численных значение энергии – это энергия излученного при этом кванта света. В нижнем поле окна модели фиксируется численное значение длины волны λ излученного или поглощенного кванта света. Подсчет стрелочек, направленных вверх или вниз, позволяет определить число спектральных линий в спектре поглощения или излучения, соответственно. На рисунке 1 представлены три линии излучения и три линии поглощения. В этой модели обязательно использование кнопки «Сброс», которая очищает окно планетарной модели.

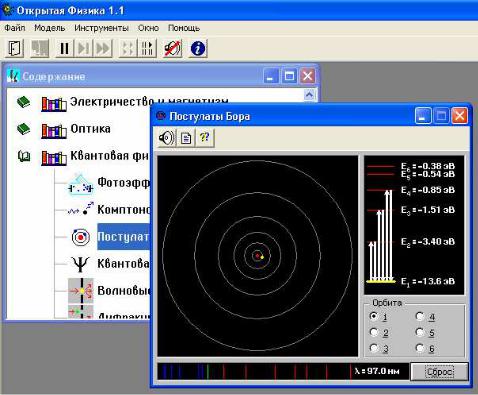
30

Рис. 46. Окно компьютерной модели «Постулаты Бора».

Порядок выполнения работы

1.Запустите, дважды щелкнув мышью, виртуальный эксперимент «Постулаты

Бора».

2.Нажмите мышью кнопку «Сброс».

3.Подведите маркер мыши к уровню энергии электрона с номером n0 ( в

модели это соответствует номеру орбиты) указанным в таблице 1 для вашего варианта. и

нажмите левую кнопку мыши; при этом в нижнем поле будет указана длина волны поглощенного кванта света, а справа вверху – значение энергии электрона на соответствующем энергетическом уровне.

каждом переходе наблюдайте и зарисуйте мигающие стрелки на модели атома водорода (в

левом верхнем поле изображена планетарная модель атома), а также стрелки в правом поле (значения энергии электрона на соответствующей энергетической орбите ni) и