
Павлов Р.М. ДЗ3
.docx|
|
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ «МИСиС» |
Практическое задание №3
По курсу метрология, технические измерения и приборы.
Студент: Павлов Р.М.
Группа: МЧ-08-1
Преподаватель: Киндоп В.Э.
Москва 2011 г.
Задача 3.2.5
Экспрессный способ определения содержания углерода в металле основан на зависимости концентрации этого компонента от температуры кристаллизации расплава. С целью установления зависимости между названными параметрами выполнены совместные измерения температуры ликвидус и содержания углерода. Результаты измерений:
|
[C] ,% |
0,97 |
0,84 |
0,77 |
0,69 |
0,57 |
0,48 |
0,35 |
0,28 |
0,19 |
0,08 |
|
tл
, |
1454 |
1473 |
1475 |
1480 |
1491 |
1497 |
1507 |
1514 |
1521 |
1531 |

Определить параметры уравнения , описывающего зависимость между содержанием углерода и температурой ликвидус: [C]=f(tл).
Решение :

II. Уравнение будет иметь следующий вид : Y=A1X1+A2
V.
Оценивание параметров Ak
:
 =2
=2 =
=
 =2
=2
 =2
=2
После
преобразование имеем :
 +
+ =
=
 +
+ n=
n=
|
|
 =14943
=14943
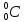
 =22334607
=22334607

 =7735,92
=7735,92
 =5.22
=5.22
 +
+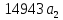 =7735,92
=7735,92
 +
+ =5.06
=5.06
|
|
|
114943 |
|
|
|
Δ = |
|
|
=52821 |
|
|
|
14943 |
10 |
|
|
Полученная система уравнения решается методом Крамера
|
|
7735,92 |
14943 |
|
|
|
Δ1 = |
|
|
=-643,26 |
|
|
|
5.22 |
10 |
|
|
|
|
|
7735,92 |
|
|
|
|
Δ2 = |
|
|
=988796 |
|
|
|
|
14943 |
5.22 |
|
|
|
|
Искомое уравнения : Y=-0,0121X+18,72 .Подставив в это уравнение среднее значения X и Y имеем:0,522=-0,0121*1494,3+18.72=0,522 VI. Вычисляются остаточные погрешности условных уравнений.
VII.
Определяется оценка дисперсии
условных уравнений.
VIII.
Определяется оценка дисперсии
параметров
IX.
Вычисляются
доверительные погрешности оцениваемых
параметров по
Выбираем
доверительную вероятность
P=0.95;ч.с.с.=10-2=8;
Определяем по
таблицам Стьюдента
X:
Результаты
окончательной оценки параметров
Переходя к исходным величинам, получим:
[C]=
=-(12 Проверка:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑x1i= |
4,94 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑(x1i)2= |
24,40 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑x1iyi= |
7327,19 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑yi= |
14967,00 |
||||||||||||||||||||||||||||||||||||||||||||||||||
Задача 3.1.5
Содержание СО2 по сечению доменной печи характеризует распределение рудной составляющей, а также зависящие от него распределение газового потока. В то же время теплообмен между газом и шихтой в верхней части шихты зависит от структуры и газопроницаемости слоя материалов, т.е. от распределения рудной составляющей. Таким, температура газа по сечению доменной печи, характеризуя распределение газового потока, также даст и распределение рудной составляющей. С целью установления зависимости между температурой газа по сечению газового потока (tр) и содержанием СО2 были выполнены одновременно измерения этих параметров и полученные результаты, представленные в таблице
|
[C] ,% |
4 |
5 |
6 |
9 |
12 |
16 |
17 |
19 |
21 |
23 |
|
tp
, |
850 |
830 |
800 |
730 |
680 |
580 |
660 |
520 |
480 |
430 |
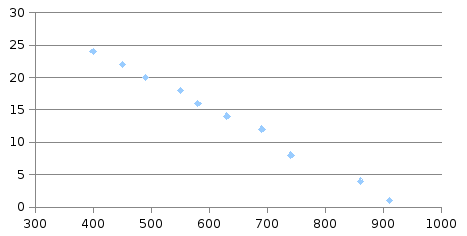
Определить параметры уравнения , описывающего зависимость между содержанием углерода и температурой ликвидус: [C]=f(tp).
Решение :

II. Уравнение будет иметь следующий вид : Y=A1X1+A2
V.
Оценивание параметров Ak
:
 =2
=2 =
=
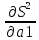 =2
=2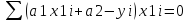
 =2
=2
После преобразование
имеем :
 +
+ =
=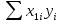
 +
+ n=
n=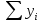
|
|
 =6560
=6560
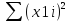 =4504400
=4504400
 =77430
=77430
 =132
=132
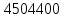 +
+ =77430
=77430
 +
+ =5.05
=5.05
|
|
|
1 |
|
|
|
Δ = |
|
|
=2608000 |
|
|
|
|
10 |
|
|
Полученная система уравнения решается методом Крамера
|
|
77430 |
6560 |
|
|
|
Δ1 = |
|
|
=-117200 |
|
|
|
132 |
10 |
|
|
|
|
|
77430 |
|
|
|
|
Δ2 = |
|
|
=110087200 |
|
|
|
|
|
132 |
|
|
|
|
Искомое уравнения : Y=-0,0449X+42,2113 .Подставив в это уравнение среднее значения X и Y имеем:13,9=-0,0449*630+42,2113= 13,9. VI. Вычисляются остаточные погрешности условных уравнений.
VII.
Определяется оценка дисперсии
условных уравнений.
VIII.
Определяется оценка дисперсии
параметров
IX.
Вычисляются
доверительные погрешности оцениваемых
параметров по
Выбираем
доверительную вероятность
P=0.95;ч.с.с.=10-2=8;
Определяем по
таблицам Стьюдента
X:
Результаты
окончательной оценки параметров
Переходя к исходным величинам, получим:
[C]=
-(0,0449 Проверка:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑x1i= |
4,94 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑(x1i)2= |
24,40 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∑x1iyi= |
7327,19 |
||||||||||||||||||||||||||||||||||||||||||||||||||




 =
= =
= =-0.012178
=-0.012178 =
= =
=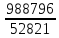 =18.72
=18.72 i
i
 0,0513593
0,0513593 =
= =
= =0.0064199
=0.0064199 ;
; =10
;
=10
;
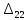 =
=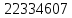 .
. =
= =
= *0.0064199=0,00000121;
*0.0064199=0,00000121;
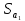 =0.001214.
=0.001214. =
= =
=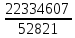 *0.0064199=2.7145;
*0.0064199=2.7145;
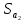 =1,647.
=1,647. –
критерию Стьюдента при заданной
доверительной вероятности P=0.95
и числе степеней свободы (n-l):
–
критерию Стьюдента при заданной
доверительной вероятности P=0.95
и числе степеней свободы (n-l): =
=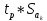
 2.306;
2.306; =
=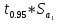 =2.306*0.001214=0,0028
=2.306*0.001214=0,0028 =
= =2.306*1,647=3,8.
=2.306*1,647=3,8. записываются в виде :
записываются в виде :
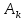 =
= ;
;
 =
= =
-0.012178
=
-0.012178 0,0028=-(12,178
0,0028=-(12,178 2,8)*
2,8)* ;
;
 =
= =18,72
=18,72 3,8;
3,8;
 0,5)*
0,5)* +(18,092
+(18,092 3,640).
3,640).






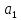 =
= =
= =-0,0449
=-0,0449 =
=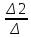 =
= =42,2113
=42,2113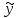 i
i
 2,2253129
2,2253129 =
= =
= =0,278164
=0,278164 ;
; =10
;
=10
;
 =
= .
. =
= =
= *0,278164=0,000001067;
*0,278164=0,000001067;
 =0,001032.
=0,001032. =
= =
= *0,278164=0,45;
*0,278164=0,45;
 =0,6717.
=0,6717. –
критерию Стьюдента при заданной
доверительной вероятности P=0.95
и числе степеней свободы (n-l):
–
критерию Стьюдента при заданной
доверительной вероятности P=0.95
и числе степеней свободы (n-l): =
=
 2,306;
2,306; =
= =2,306*0,001032
=2,306*0,001032 ;
;
 =
=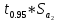 =2,306*0,6717=1,5489.
=2,306*0,6717=1,5489. записываются в виде :
записываются в виде :
 =
= ;
;
 =
= =
-0,0449
=
-0,0449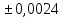
 =
=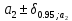 =42,2113
=42,2113
 1,5489;
1,5489;
 *tp+(42,2113
*tp+(42,2113
 1,5489).
1,5489).