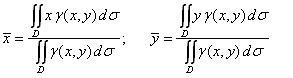3 Приложения двойных интегралов

3 Приложения двойных интегралов

3.1 Теоретическое введение

Рассмотрим приложения двойного интеграла к решению ряда геометрических задач и задач механики.

3.1.1 Вычисление площади и массы плоской пластины

Рассмотрим тонкую материальную пластину D, расположенную в плоскости Оху. Площадь S этой пластины может быть найдена с помощью двойного интеграла по формуле:

­ ­ ­

(1)

Пусть в каждой точке пластины задана ее поверхностная плотность γ = γ (x, y) ≥ 0. Будем считать, что функция γ = γ (x, y) непрерывна в области D. Тогда масса m этой пластины равна двойному интегралу от функции плотности γ (x, y) по области D:

­ ­ ­

(2)

3.1.2 Статические моменты. Центр масс плоской пластины

Статическим моментом M_x относительно оси Ox материальной точки P(x;y), лежащей в плоскости Oxy и имеющей массу m, называется произведение массы точки на ее ординату, т.е. M_x= my. Аналогично определяется статический момент M_y относительно оси Oy: ­ ­ ­ M_y = mx. Статические моменты плоской пластины с поверхностной плотностью γ = γ (x, y) вычисляются по формулам:

­ ­ ­

(3)

­ ­ ­

(4)

Как известно из механики, координаты x_c , y_c центра масс плоской материальной системы определяются равенствами:

­ ­ ­

(5)

где m – масса системы, а M_x и M_y – статические моменты системы. Масса плоской пластины m определяется формулой (1), статические моменты плоской пластины можно вычислить по формулам (3) и (4). Тогда, согласно формулам (5), получаем выражение для координат центра масс плоской пластины:

­ ­ ­

(6)

3.2 Содержание типового расчета

Типовой расчет содержит две задачи. В каждой задаче задана плоская пластина D, ограниченная линиями, указанными в условии задачи. Г(x,y) – поверхностная плотность пластины D. Для этой пластины найти: 1. S – площадь; 2. m – массу; 3. M_y , M_x – статические моменты относительно осей Оy и Ох соответственно; 4. , – координаты центра масс.

3.3 Порядок выполнения типового расчета

При решении каждой задачи необходимо: 1. Выполнить чертеж заданной области. Выбрать систему координат, в которой будут вычисляться двойные интегралы. 2. Записать область в виде системы неравенств в выбранной системе координат. 3. Вычислить площадь S и массу m пластины по формулам (1) и (2). 4. Вычислить статические моменты M_y , M_x по формулам (3) и (4). 5. Вычислить координаты центра масс , по формулам (6). Нанести центр масс на чертеж. При этом возникает визуальный (качественный) контроль полученных результатов. Численные ответы должны быть получены с тремя значащими цифрами.

3.4 Примеры выполнения типового расчета

Задача 1. Пластина D ограничена линиями: y = 4 – x²; х = 0; y = 0 (x ≥ 0; y ≥ 0) Поверхностная плотность γ₀ = 3. Решение. Область, заданная в задаче, ограничена параболой y = 4 – x², осями координат и лежит в первой четверти (рис. 1). Задачу будем решать в декартовой системе координат. Эта область может быть описана системой неравенств:

Рис. 1

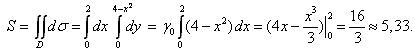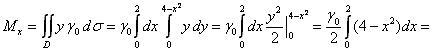
Площадь S пластины равна (1): Так как пластина однородная, ее масса m = γ₀S = 3· = 16. По формулам (3), (4) найдем статические моменты пластины: Координаты центра масс находятся по формуле (6): Ответ: S ≈ 5,33; m = 16; M_x = 25,6; M_y = 12; = 0,75; = 1,6.

Задача 2. Пластина D ограничена линиями: х² + у² = 4; х = 0, у = х ( х ≥ 0, у ≥ 0). Поверхностная плотность γ(x,y) = у. Решение. Пластина ограничена окружностью и прямыми, проходящими через начало координат (рис. 2). Поэтому для решения задачи удобно использовать полярную систему координат. Полярный угол φ меняется от π/4 до π/2. Луч, проведенный из полюса через пластину, «входит» в неё при ρ = 0 и «выходит» на окружность, уравнение которой: х² + у² = 4 <=> ρ = 2.

Рис. 2

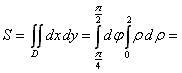
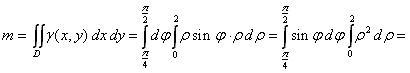
Следовательно, заданную область можно записать системой неравенств: Площадь пластины найдем по формуле (1): Массу пластины найдем по формуле (2), подставив γ(x,y) = у = ρ sinφ: Для вычисления статических моментов пластины используем формулы (3) и (4): Координаты центра масс получим по формулам (6): Ответ: S ≈ 1,57; m ≈ 1,886; M_x = 2,57; M_y = 1; = 0,53; = 1,36.

3.5 Оформление отчета

В отчете должны быть представлены все выполненные расчеты, аккуратно выполненные чертежи. Численные ответы должны быть получены с тремя значащими цифрами.