3.3. Проверка (Mathcad). Вывод
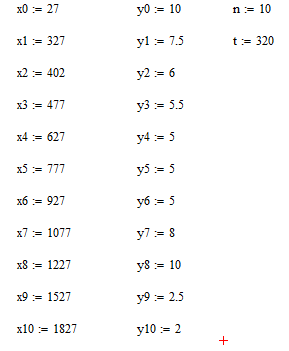
Приближенное значение функции в точке t=320 равно 7,77. В то время как в C# значение функции в этой же точке равно 7,62. Это говорит о том, что задача решена верно.
Задача №4. Аппроксимация. Исходные данные
|
|
f(x)=a*ln(x)+b |
|
|
|
|
| ||
|
x |
1965 |
1966 |
1967 |
1968 |
1969 |
1970 |
1971 |
1972 |
|
y |
212 |
235 |
345 |
252 |
255 |
295 |
333 |
426 |
4.1. Описание использованного метода (Метод Жордана-Гаусса)
Метод Гаусса-Жордана (метод полного исключения неизвестных) - метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. (Метод является модификацией метода Гаусса.)
Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение (верхнее число не должно быть равно 0).
Все элементы первой строки делят на верхний элемент выбранного столбца.
Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.
Далее проводят такую процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
После
повторения этой процедуры
раз
получают верхнюю треугольную матрицу
Вычитают из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора.
Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.
4.2. Текст задачи
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
namespace ConsoleApplication13
{
class Program
{
static void Main(string[] args)
{
int j, i;
int m = 2; // Количество определяемых коэффициентов
double f, delta = 0;
int n = 8; // число аппроксимационных точек
double[] x = new double[] { 1965, 1966, 1967, 1968, 1969, 1970, 1971, 1972 };
double[] y = new double[] { 212, 235, 345, 252, 255, 295, 333, 426 };
double[] c = new double[m + 1];
double[,] a = new double[m + 1, m + 1];
// Заполнение значениями расширенной матрицы a[i,i]
for (i = 0; i <= m; i++) for (j = 0; j <= m; j++) a[i, j] = 0;
for (i = 0; i < n; i++)
{
a[0, 0] = a[0, 0] + 1;
a[0, 1] = a[0, 1] + Math.Log(x[i]);
a[0, 2] = a[0, 2] + y[i];
a[1, 0] = a[1, 0] + Math.Log(x[i]);
a[1, 1] = a[1, 1] + Math.Log(x[i]) * Math.Log(x[i]);
a[1, 2] = a[1, 2] + Math.Log(x[i]) * y[i];
}
Console.WriteLine("Результаты программы последовательно выводятся с помощью клавиши Enter");
Console.WriteLine(" Коэффициенты расширенной матрицы СЛАУ \n");
PrintMX(a, m);
// решаем СЛАУ(созданную матрицу a[m+1,m+1]) и результат сохраняем в c[m]
Gaus(a, c, m);
// Проверочная печать коэффициентов с[i]
Console.WriteLine(" Коэффициенты аппроксимирующей функции \n");
for (i = 0; i < m; i++)
Console.WriteLine(" c[{0,1:f0}]={1,7:f5}", i, c[i]);
Console.ReadKey();
// Вывод таблицы Аппроксимированной функции Y от X
Console.WriteLine("\n Значение аппроксимирующей функции");
Console.WriteLine(" вида f(x)=({0,7:f5}*ln(x)+{1,7:f5})\n", c[1], c[0]);
Console.WriteLine(" Xi Yi f(Xi) Относительная невязка ");
delta = 0;
for (i = 0; i < n; i++)
{
f = fx(x[i], c);
delta = Math.Abs((f - y[i]) / f);
Console.WriteLine("{0,10:f4} {1,10:f4} {2,10:f4} {3,10:f4}", x[i], y[i], f, delta);
}
Console.ReadLine();
}
// функция решения СЛАУ методом Гаусса, а - матрица, х - вектор результата, n - порядок матрицы
// столбец a[i,n] содержит свободные члены
static void Gaus(double[,] a, double[] x, int n)
{
int i, j, k;
double c;
for (i = 0; i < n; i++)
for (j = i + 1; j < n; j++)
{
c = a[j, i] / a[i, i];
for (k = i; k <= n; k++) a[j, k] = a[j, k] - c * a[i, k];
// PrintMX(a, n);
}
// получаем вектор коэффициентов x[n-1] обратным ходом
// помним, что столбец a[i,n] содержит свободные члены, а строка a[n,i] не определена
for (i = n - 1; i >= 0; i--)
{
x[i] = a[i, n] / a[i, i];
for (j = n - 1; j >= i && i > 0; j--) a[i - 1, n] = a[i - 1, n] - a[i - 1, j] * x[j];
}
}
// Аппроксимирующая функция f(x) при известных коэффициентах c[i]
// (полученых после решения матрицы СЛАУ Гауссом)
static double fx(double x, double[] c)
{
return (c[1] * Math.Log(x) + c[0]);
}
static void PrintMX(double[,] a, int m)
{
Console.WriteLine();
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <= m; j++) Console.Write(" {0,10:f5}", a[i, j]);
Console.WriteLine();
}
Console.ReadLine();
}
}
}