10.8. Экстерналии в квазилинейной экономике |
370 |
Укажем также возможные Парето-улучшения для состояния равновесия для данного случая. Пусть ((dx, dz), (dy, dr), da) — дифференциально малое изменение для состояния равновесия, причем
dx = 0, dy = 0, dai = 0 i, daj = 0 j 6= j , daj e = 0 e 6= e .
Тогда эффект изменения производства экстерналии aj e на величину daj e окажется равным εdaj e . Пусть, например, предельный эффект экстерналии aj e положителен (ε > 0). Тогда если daj e > 0, то величина εdaj e положительна. Она представляет собой экономию блага (l + 1) в результате указанного увеличения производства экстерналии e производителем j .
Изменение должно быть таким, чтобы новое состояние было допустимым. Это требование определяет соотношения, которым должны удовлетворять изменения. Так, дифференцируя баланс по (l + 1)-му благу, получим
XX
dzi + |
drj = 0. |
i I |
j J |
Изменение производства экстерналии вызывают изменения затрат (l + 1)-го блага на предприятиях:
∂cj(y¯j, a¯)
drj = ∂aj e daj e ,
причем drj = 0, поскольку в равновесии ∂cj (y¯j , a¯)/∂aj e = 0. Полезности потребителей при этом меняются на величины
dui = dvi + dzi = ∂vi(x¯i, a¯)daj e + dzi.
Сумма изменений полезностей с учетом соотношений между изменениями равна εdaj e . Действительно,
Xi I dui = Xi I |
∂v (x¯ , a¯) |
daj e + Xi I dzi = . |
||||
i |
i |
|
||||
∂a |
j e |
|||||
= ( |
|
∂cj(y¯j, a¯) |
+ ε)daj e − drj = . |
|||
|
∂aj e |
|||||
J |
|
|
|
|
|
j J |
jX |
|
|
|
|
|
X |
X |
drj + εdaj e − |
X |
||||
= |
drj = εdaj e . |
|||||
j J |
|
|
|
|
|
j J |
Существуют такие {dzi}, что все dui положительны. Если, например,
dzi = εdaj e /m − ∂vi(x¯i, a¯)daj e i, ∂aj e
то
dui = εdaj e /m > 0 i.
Понятно, что если равновесие с налогами Парето-оптимально, то величина, например, ставки налога, взимаемого с производителя j за выпуск единицы экстерналий должна быть равна предельному эффекту экстерналий, взятому со знаком минус, т. е.
X |
∂vi |
X6 |
∂cs |
|
|
∂aje |
∂aje . |
||||
tje = − i I |
+ s=j |
||||
Аналогично для экстерналии, производимой потребителем,
X6 |
∂vs |
X |
∂cj |
|
|
∂aie |
∂aie . |
||||
tie = − s=i |
+ j J |
||||
10.8. Экстерналии в квазилинейной экономике |
371 |
Это вариант правила Пигу для квазилинейной экономики.
Обратно, если ставки налогов на производство экстерналий удовлетворяют правилу Пигу, то равновесие с налогами Парето-оптимально при дополнительных предположениях о том, что функции полезности вогнуты, а функции издержек выпуклы.
Цены экстерналий в равновесии с торговлей экстерналиями удовлетворяют соотношениям
qise = − ∂vs , i, s 6= i, e Ei, ∂aie
qije = ∂cj , i, j, e Ei, ∂aie
qjie = − ∂vi , j, i, e Ej, ∂aje
qjse = ∂cs , j, s 6= j, e Ej, ∂aje
то есть совпадают с соответствующим «предельным ущербом» от экстерналии.
Если равновесие в экономике с налогами и равновесие в экономике с торговлей экстерналиями соответствуют одному и тому же состоянию экономики, то налоги и цены экстерналий связаны соотношениями
XX
tie = |
qise + qije. |
s6=i |
j J |
XX
tje = − qjie + |
qjse, |
i I |
s6=j |
Заметим, что если функции полезности вогнуты, а функции издержек выпуклы, причем хотя бы одна из них строго, то величины налогов Пигу и цен экстерналий не зависят от состояния равновесия и рассчитываются по указанным выше формулам на решении задачи (WE).
Интерес представляет также частный случай, когда воздействие экстерналий на благосостояние потребителей и производственные возможности производителей не зависит от уровня потребления и производства обычных благ, т. е. ситуацию, когда функции полезности и функции издержек имеют следующий вид (сепарабельны):
ui(xi, zi, ai, a−i) = vi(xi, ai, a−i) + zi = vix(xi) + via(a) + zi,
cj(yj, aj, a−j) = cjy(yj) + cja(a).
В этом случае объем производства и потребления всех обычных благ (кроме квазилинейного блага) не зависит от типа равновесия (один и тот же, как в «обычном» рыночном равновесии, так и в равновесии с налогами и в равновесии с торговлей экстерналиями), хотя производство и потребление экстерналий в этих состояниях могут различаться. Более того, рынки сепарабельных экстерналий можно анализировать независимо от рынков обычных благ.
Пример 49 ((Курильщик и некурящий)):
Модифицируем Пример 47 для квазилинейной экономики с сепарабельными экстерналиями. Пусть функции полезности студентов имеют вид
ui = vix(xi) + via(a) + zi, i = 1, 2,
где xi — объемы потребления «обычных» благ, zi — количество денег на остальные блага, a > 0 — количество выкуриваемых первым из них сигарет. Как и ранее, второй участник —
некурящий, и v20 a(a) < 0, а у первого, напротив, v10 a(a) > 0, если количество сигарет меньше aˇ (aˇ > 0) и v10 a(a) < 0, если a > aˇ.
10.8. Экстерналии в квазилинейной экономике |
372 |
Как уже говорилось, можно «забыть» о существовании благ xi и сосредоточится на экстерналии a и квазилинейном благе zi . Поскольку ситуация фактически «двумерная», то она, как и ранее, иллюстрируется с помощью Рис. 10.1 (только по горизонтальным осям откладывается zi ).
В точке A, соответствующей абсолютному праву некурящего на чистый воздух (a = 0) имеют место неравенства v20 a(0) < 0 < v10 a(0).
Если выполнено −v20 a(0) < v10 a(0) (т. е. предельный ущерб от экстерналий не слишком велик — не превышает предельной оценки курения для курильщика), то состояние A не оптимально. Действительно, оптимум должен характеризоваться максимумом частичного индикатора благосостояния
W (a) = v1a(a) + v2a(a).
В граничном Парето-оптимуме (a = 0) должно быть выполнено W 0(0) 6 0, т. е. −v20 a(0) >
v10 a(0).
Из этого состояния можно произвести строгое Парето-улучшение вида da > 0, dz2 > 0,
dz1 = −dz2 < 0. При этом |
|
|
|
|
|
|
|
|
|
|
dv |
= v0 |
(0)da |
− |
dz |
, |
dv |
2 |
= v0 |
(0)da + dz |
. |
1 |
1a |
|
2 |
|
|
2a |
2 |
|
Для того, чтобы одновременно dv1 > 0 и dv2 > 0, нужно выбрать dz2 так, чтобы
−v20 a(0)da < dz2 < v10 a(0)da.
В точке B, соответствующей праву свободно курить (a = aˇ), выполнено v10 a(ˇa) = 0, v20 a(ˇa) < 0. Ясно, что при этом условие оптимальности W 0(ˇa) = 0 не выполнено. Парето-улучшение должно иметь вид da < 0, dz1 > 0, dz2 = −dz1 < 0. При этом
|
|
|
dv |
1 |
= dz |
, |
dv |
2 |
= v0 |
(ˇa)da |
− |
dz |
. |
|
|
|
|
|
|
1 |
|
|
2a |
|
1 |
|
|
|
|||
|
|
Некурящий улучшит свое благосостояние (dv2 > 0) при dz1 < v20 a(ˇa)da. |
|
|
|||||||||||
− |
|
Внутреннее равновесие с торговлей экстерналиями характеризуется соотношениями v20 a(¯a) = |
|||||||||||||
q |
1a |
(¯a) = q, где a¯ — количество дыма в этом равновесии. При этом W 0 |
(¯a) = 0. |
4 |
|||||||||||
|
и v0 |
|
|||||||||||||
Пример 50 ((Экстерналии в производстве, частное равновесие)):
Рассмотрим квазилинейную экономику с 3 благами (l = 2) и двумя производителями, производящих 1-е и 2-е блага соответственно, затрачивая 3-е благо. Их функции издержек зависят от некоторых действий первого производителя (например, действий по уменьшению загрязнений, которые (загрязнения) негативно влияют на условия деятельности второго производителя.
Будем предполагать, что объем загрязнений, произведенных первым производителем, однозначно определяется объемом выпускаемой им продукции y1 > 0 и поэтому можем быть измерен этим объемом. Тем самым мы возвращаемся к подходу, обсужденному в первом параграфе данной главы. Будем считать также, что внешнее влияние первого предприятия на второе увеличивает издержки 2-го предприятия на одну и ту же величину, независимо от выпуска этого предприятия:
c1 = c1(y1) и c2 = c22(y2) + c21(y1)
причем c021(y1) > 0.
В дальнейшем будем также предполагать выполненными стандартные предположения неоклассического анализа, а именно, предельные издержки обоих производителей положительны
c01(y1) > 0, c022(y2) > 0,
10.8. Экстерналии в квазилинейной экономике |
373 |
и не убывают по объемам производства. Потребительский спрос порождается репрезентативным потребителем с сепарабельной функцией полезности
u = v1(x1) + v2(x2) + z,
такой что предельные полезности vk0 (x) положительны и убывают.
Проиллюстрируем на этом простом примере все рассмотренные нами инструменты корректировки фиаско рынка.
Парето-оптимум.
Индикатор благосостояния для данной экономики имеет вид
W = v1(y1) + v2(y2) − c1(y1) − c22(y2) − c21(y1).
Дифференцируя его, получаем следующую дифференциальную характеристику Парето-опти-
мальных состояний:
v10 (ˆy1) = c01(ˆy1) + c021(ˆy1), v20 (ˆy2) = c022(ˆy2).
Если общие издержки c01(y1)+c021(y1) не убывают, то при сделанных выше предположениях, эта дифференциальная характеристика однозначно определяет объемы производства первых двух благ в Парето-оптимальных состояниях. Поэтому мы можем говорить о Парето-оптимальных объемах производства yˆ1 и yˆ2 .
Рыночное равновесие.
Поскольку обратные функции спроса и обратные функции предложения имеют вид:
pD1 (y1) = v10 (y1), pD2 (y1) = v20 (y2), pS1 (y1) = c01(y1), pS2 (y1) = c022(y2),
то рыночное равновесие определяет следующая дифференциальная характеристика (равенство цен спроса и предложения на обоих рынках):
v10 (¯y1) = c01(¯y1),
v20 (¯y2) = c022(¯y2).
Сепарабельность функции полезности приводит к независимости объемов спроса и предложения первого и второго блага от других благ и поэтому позволяет анализировать их рынки независимо друг от друга. В дальнейшем мы будем характеризовать только рынок первого блага, так как характеристики рынка второго не зависят от выбранных способов регулирования первого. Заметим также, что отсутствие внешнего влияния первого производителя на второго приводит к тому, что производство второго блага в рыночном равновесии равно его количеству в каждом Парето-оптимальном состоянии y¯2 = yˆ2 (Парето-оптимальному количеству). С другой стороны, сравнивая характеристики равновесного и Парето-оптимального количества первого блага, можем заключить, что при сделанных предположениях относительно внешних влияний (отрицательные экстерналии) выполнено yˆ1 < y¯1 . Это следует из того, что функция
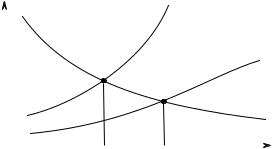
v10 (y1) − c01(y1) убывает, равна c021(ˆy1) > 0 при y1 = yˆ1 и равна 0 при y1 = y¯1 .
Рис. 10.2 показывает оптимальный yˆ1 и равновесный y¯1 выпуски первого производителя и иллюстрирует причину фиаско рынка: первый производитель в своих расчетах издержек и дохода принимает во внимание только часть действительных предельных издержек, связанных с производством первого блага. Здесь c01(y1) — частные предельные издержки 1-го предприятия, а c01(y1) + c021(y1) — общественные предельные издержки. Разница, c021(y1), соответствует предельному ущербу от экстерналии.
10.8. Экстерналии в квазилинейной экономике |
374 |
||||||
|
pD(y |
1 |
)=v0 (y |
1 |
) |
c10 (y1)+c210 (y1) |
|
|
|||||||
|
1 |
1 |
|
||||
|
|
|
|
|
|
c10 (y1) |
|
|
|
|
|
|
|
|
|
yˆ1 |
y¯1 |
y1 |
Рис. 10.2.
Квотирование.
При количественном ограничении (квоте) на объем выпуска первого производителя в размере y˜1 = yˆ1 равновесие с квотами на рынке 1-го блага установится при цене p1 = p1(ˆy1) и объеме производства yˆ1 .
Налог Пигу.
Ставка налога Пигу на загрязнение равна
t = c021(ˆy1),
поскольку при таком налоге равновесие с налогами Парето-оптимально. Действительно, решением задачи 1-го производителя,
Π1(y1) = p1y1 − c1(y1) − ty1 → max,
при цене первого блага p1 = pD1 (ˆy1) является величина yˆ1 .
Дотации за сокращение загрязнений.
Другое возможное решение проблемы экстерналий — дотации за уменьшение объема их производства ниже некоторой установленной квоты y˜1 . Пусть s — ставка такого дотационного возмещения. Тогда прибыль от выпуска y1 единиц продукции в условиях дотаций приносит прибыль в размере
Π1(y1) = p1y1 − c1(y1) + s(˜y1 − y1),
и поэтому достигает максимального размера при объеме выпуска y1 (единиц продукции), который определяется из уравнения
p1 = c01(y1) + s.
Как и выше, ставка дотационных выплат в размере s = c021(ˆy1) при цене первого блага p1 = pD1 (ˆy1) обеспечивает производство оптимального объема продукции yˆ1 (и оптимального объема экстерналий). Это означает, что p1 = pD1 (ˆy1) — цена равновесия на рынке 1-го блага при таком выборе ставки дотаций.
Заметим, что величина квоты не влияет на равновесие на рынке первого блага. При y˜1 = 0 дотация оказывается налогом, так как в равновесии y1 > y˜1 = 0.
Торговля экстерналиями.
Напомним, что К. Эрроу видел проблему экстерналий в отсутствии рынка экстерналий. Предположим, что существует рынок экстерналий и пусть цена единицы экстерналии составляет q. Объем производства экстерналий обозначим a.
Тогда задача первого производителя имеет вид
Π1 = p1y1 − qa − c1(y1) → max, y1 = a,
y1,a