/34. Покажите, что если неоклассические предпочтения заданы на конечном множестве альтернатив, то в этом множестве существует как наименьшая (наихудшая), так и наибольшая (наилучшая) альтернатива. (Этот факт был использован в доказательстве Теоремы 7.)

/35. В Теореме 7 докажите, рассмотрев все возможные случаи, что построенная функция является функцией полезности.

/36. Докажите, что если множество кривых безразличия для некоторых неоклассических предпочтений счетно, то существует функция полезности, представляющая эти предпочтения.

/37. Пусть X = X1 × X2 , где X1 = {1, 2, . . .}, а X2 — множество всех рациональных чисел между 0 и 1. Пусть на парах из X введено лексикографическое упорядочение. Докажите, что существует функция полезности, отвечающая этому упорядочению. Запишите ее явную формулу.

/38. Борис Бенедиктович Бахвалин на основании полного, транзитивного и непрерывного нестрогого отношения предпочтения построил следующую функцию полезности:

Покажите, что эта функция не является непрерывной. Нет ли здесь противоречия с непрерывностью предпочтений? Возможно ли на основании этих же предпочтений построить непрерывную функцию? Если да, то постройте ее, если нет, то поясните, почему построение невозможно.

/39. Продемонстрируйте, что лексикографические предпочтения на R2+ не являются непрерывными, построив конкретные последовательности наборов {xn}, {yn}, которые бы противоречили Определению 8.

/40. Покажите, что если функция полезности u(x) непрерывна, то предпочтения, породившие эту функцию полезности, также являются непрерывными.

/41. Закончите доказательство Теоремы 8, показав, что для построенных окрестностей Vx

и Vy , справедливо, что для любых x0 Vx ∩ X и y0 Vy ∩ X выполнено x0 y0 .

/42. Пусть на выпуклом множестве X заданы непрерывные предпочтения, и пусть для наборов x, y X выполнено x y. Докажите, что найдется набор z X , такой что x z y.

/43. Покажите, что функция полезности монотонна тогда и только тогда, когда монотонны представляемые ею предпочтения.

2.5Свойства предпочтений и функции полезности

Впредыдущем параграфе мы уже дали определение ряда важных свойств предпочтений, а именно, непрерывности, монотонности и строгой монотонности26. При анализе конкретных микроэкономических задач часто возникает необходимость делать дополнительные предположения о предпочтениях или о функциях полезности. В данном параграфе мы обсудим наиболее часто используемые предположения о свойствах предпочтений и покажем их связь с соответствующими свойствами функции полезности, которая представляет эти предпочтения.

Иногда, в ситуациях, когда предположение о строгой монотонности предпочтений выглядит ограничительным, предполагается выполнение более слабого свойства — локальной ненасыщаемости. Выполнение этого свойства во многих случаях оказывается достаточным для

26Можно также ввести свойство, промежуточное между монотонностью и строгой монотонностью. См. определение полустрогой монотонности в сноске к Теореме 66 в гл. 5.

доказательства тех свойств выбора, которые следуют из строгой монотонности предпочтений.

Определение 11:

Предпочтения называются локально ненасыщаемыми, если для любого допустимого набора x X в любой его окрестности найдется другой допустимый набор xˆ X , такой что xˆ x.

Отметим, что выполнение свойства локальной ненасыщаемости запрещает два типа предпочтений:

•предпочтений c точкой насыщения, т. е. с потребительским набором, который является наилучшим выбором потребителя среди всех ближайших наборов (см. Рис. 2.5);

x2

точка

насыщения

x1

Рис. 2.5. Предпочтения с точкой (глобального) насыщения

•предпочтений с «толстой» кривой безразличия, когда существует окрестность некоторого набора, в которой все наборы эквивалентны для потребителя (см. Рис. 2.6).

x2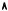

x1

Рис. 2.6. «Толстая» кривая безразличия

Связь между понятиями строгой монотонности и локальной ненасыщаемости, в принципе, очевидна. Если предпочтения являются строго монотонными, то они локально ненасыщаемы. Обратное, вообще говоря, неверно.

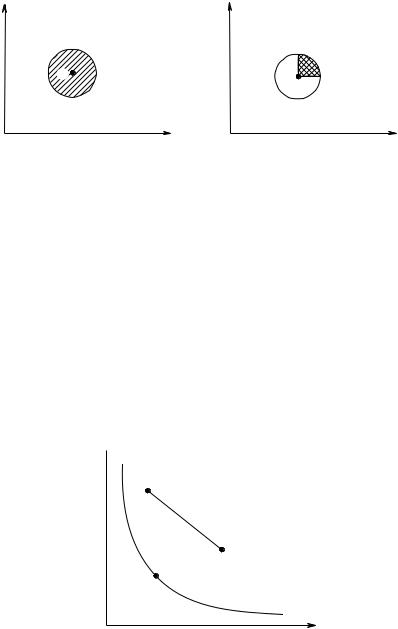
Рис. 2.7 показывает разницу между понятиями строгой монотонности и локальной ненасыщаемости. Для заданной окрестности набора x заштрихованная область на первой части рисунка показывает ту зону, в которой могут находиться лучшие наборы при выполнении свойства локальной ненасыщаемости. Аналогично, заштрихованная область на второй части

Рис. 2.7. Сравнение строгой монотонности и локальной ненасыщаемости

рисунка показывает зону, где находятся лучшие наборы для предпочтений, обладающих свойством строгой монотонности.

Следующая группа свойств предпочтений, которую мы рассмотрим, важна для демонстрации «хороших» свойств функции выбора/спроса и доказательства существования равновесия. Здесь и далее мы будем предполагать, что множество X выпукло.

Определение 12:

Предпочтения называются выпуклыми, если x, y X : x < y и 0 6 α 6 1 выполнено

αx + (1 − α)y < y.

Предпочтения называются строго выпуклыми, если x, y X : x < y, x 6= y и 0 < α < 1 выполнено αx + (1 − α)y y.

x2

x0

L+(x)

x00

x

x1

Рис. 2.8. Выпуклые предпочтения

Как несложно понять, выпуклость предпочтений эквивалентна выпуклости верхнего лебеговского множества L+(x) любого набора x. На Рис. 2.8 как x0 , так и x00 лежат в L+(x). Из выпуклости предпочтений следует, что весь отрезок между x0 и x00 лежит в L+(x).

Остановимся теперь на различии понятий строгой выпуклости от «просто» выпуклости. Ясно, что строго выпуклые предпочтения являются выпуклыми. Грубо говоря, различие между этими понятиями состоит в том, что при выполнении свойства строгой выпуклости запрещена ситуация, когда граница верхнего лебеговского множества (или, что тоже самое, кривая безразличия) имеет «линейные» части. На Рис. 2.9 изображен пример выпуклых, но не строго выпуклых предпочтений.

С понятием выпуклости предпочтений в случае, когда они представимы функцией полезности, тесно связаны свойства вогнутости и квазивогнутости функции полезности. Оказывается, что для квазивогнутой функции полезности справедлив следующий результат.

Стоит отметить, что, вообще говоря, в отличие от свойства квазивогнутости, свойство во-

гнутости не сохраняется при монотонно возрастающем преобразовании. (Требуется, чтобы

√

преобразующая функция была вогнута.) Например, функция x вогнута, но после применения к ней монотонного преобразования y4 (при y > 0) получается функция x2 , которая уже не является вогнутой, хотя и является квазивогнутой (при x > 0).

Достаточно типична ситуация, когда из квазивогнутой функции можно сделать вогнутую (например, x2 преобразованием √4 y превращается в √x). Если прорешать достаточно много типовых задач, то может сложиться впечатление, что каждая квазивогнутая функция переводится монотонно возрастающим преобразованием в вогнутую функцию и, в этом смысле, два эти класса функций эквивалентны. Однако, это не так. Например, функция

p

f(x1, x2) = (x1 − 1) + (1 − x1)2 + 4(x1 + x2) квазивогнута. Ее линии уровня — непараллельные прямые линии. Можно показать, что эта функция не может быть трансформирована в вогнутую функцию возрастающим преобразованием. Следует оговориться, что большинство подобных примеров достаточно причудливы и их построение требует достаточной изобретательности. Поэтому для того чтобы убедиться, что функция квазивогнута, рекомендуется попытаться преобразовать ее в вогнутую функцию.

Приведем пример, иллюстрирующий технику проверки вогнутости и квазивогнутости функций.

Пример 6:

Рассмотрим функцию u(x) = x1x2 , заданную на неотрицательном ортанте R2+ . Покажем, что эта функция квазивогнута, но не является вогнутой.

Способ 1 (По определению)

Возьмем два произвольных вектора x, y R2+ . Тогда для любого 0 6 α 6 1 имеем

(αx1 + (1 − α)y1)(αx2 + (1 − α)y2) =

= α2x1x2 + (1 − α)2y1y2 + α(1 − α)x1y2 + α(1 − α)x2y1

Без потери общности будем считать, что y1y2 > x1x2 . Если компоненты вектора x не равны

Однако данная матрица не является отрицательно полуопределенной. Например, для вектора z| = (1, 1) имеем z| Hz = 2 > 0. Таким образом, функция не является вогнутой.

Покажем, что она квазивогнута. Несложно увидеть, что z| Hz = 2z1z2 . Рассмотрим знак этой квадратичной формы при всех z таких, что ru(x)z = 0, т. е. при всех z таких, что x2z1 + x1z2 = 0. Умножив это равенство на z1 , получим x2(z1)2 + x1z1z2 = 0. На внутренности

ит в том, чтобы найти преобразование, которое бы сделало ее вогнутой. Как несложно заметить, возрастающее преобразование ln(·) переводит ее в вогнутую функцию. Действительно, получившаяся функция ln(x1) + ln(x2) является вогнутой, поскольку ее матрица Гессе будет

Рассмотренные выше свойства выпуклости и строгой выпуклости предпочтений тесно связаны с понятием предельной нормы замены28. Напомним, что под предельной нормой замены i-ым благом j -ого понимается величина

MRSij(x) = − u00i(x) .

uj(x)

Покажем, что из выпуклости предпочтений следует закон неубывания предельной нормы замены. При этом будем предполагать, что предпочтения потребителя представимы непрерывно дифференцируемой квазивогнутой функцией полезности u : Rn+ 7→R.

Содержательно, норма замены указывает на то количество блага j , на которое необходимо сократить потребление этого товара в обмен на увеличение потребления блага i с тем, чтобы уровень полезности потребителя и количество всех остальных товаров оставались неизменными. Таким образом, в случае если количество блага i изменяется на дифференциально малую величину dxi , то для того, чтобы потребитель остался на той же самой кривой безразличия u(x) = u¯, количество блага j при условии что количество остальных благ остается неизменным должно измениться на величину dxj такую что

u0i(x)dxi + u0j(x)dxj = 0.

Возьмем некоторую кривую безразличия и зафиксируем количества всех благ, кроме i-го и j -го. Уравнение u(x1, . . . , xi, . . . , xj, . . . , xl) = u¯ задает для данного уровня полезности u¯ зависимость xj от xi как неявную функцию xi(xj). Предельная норма замены равна наклону

функции xi(xj):

dxj(xi) = − u00i(x) = MRSij(x). dxi uj(x)

Проверим, что закон неубывания предельной нормы замены выполняется, если функция полезности квазивогнута, или, что тоже самое, предпочтения выпуклы. Для этого докажем, что функция xi(xj) выпукла.

28Возможно, что впервые связь между поведением предельной нормы замены и выпуклостью предпочтений было отмечена Джоном Хиксом и Роем Алленом: «Принцип убывающей предельной полезности должен уступить место возрастающей предельной нормой?? замены. . . . Это условие выражается на диаграмме безразличия с помощью кривых безразличия, выгнутых по направлению к осям». См. J. R. Hicks and R. G. D. Allen: A Reconsideration of the Theory of Value: Part I, Economica, New Series 1 (1934): 52–76 (рус. пер. Дж. Р. Хикс и Р. Г. Д. Аллен: Пересмотр теории ценности, в кн. Теория потребительского поведения и спроса, В. М. Гальперин (ред.), СПб.: Экономическая школа, 1993: 117–141).

Пусть x0i и x00i — некоторые количества i-го блага, и пусть x0 и x00 — наборы, в которых xi = x0i , xj = xj(x0i) и xi = x00i , xj = xj(x00i ) соответственно. Рассмотрим набор xα , являющийся

выпуклой комбинацией наборов x0 и x00 (α [0, 1]):

xα = αx0 + (1 − α)x00,

а также набор x , в котором xi = xαi = αx0i +(1−α)x00i и xj = xj(xαi ). По определению функции xi(xj) наборы x0 , x00 и x эквивалентны. С другой стороны, из выпуклости предпочтений следует, что xα < x0 x00 . Таким образом, xα < x . В наборах xα и x все блага, кроме

j -го, содержатся в одинаковых количествах. Если предположить, что функция полезности возрастает по j -му благу, то должно быть, xαj > xj(xαi ) где xαj = αxj(x0i) + (1 −α)xj(x00i ). Этим

мы доказали выпуклость функции xj(xi).

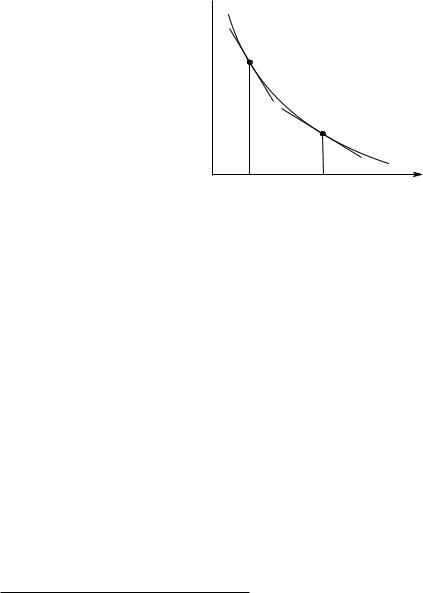
Производная выпуклой функции не убывает (см. Рис. 2.10). Таким образом, в случае выпуклости предпочтений имеем выполнение закона неубывания предельной нормы замены («убывания предельной полезности»).

xj

xj(xi)

xi

x0i x00i

Рис. 2.10. Неубывание предельной нормы замены для выпуклых предпочтений

Отметим, что в некотором смысле верно и обратное, т. е. выпуклость предпочтений эквивалентна неубыванию предельной нормы замены29.

В приложениях экономической теории очень часто рассматриваются также дополнительные свойства предпочтений, которые налагают более сильные требования на функцию полезности. Так, например, в макроэкономике при рассмотрении поведения агрегированного потребителя часто предполагается выполнение свойства гомотетичности.

Определение 13:

Предпочтения называются гомотетичными, если

• для каждого положительного t tx X тогда и только тогда, когда x X .

•для каждого положительного t соотношение tx ty выполняется тогда и только тогда, когда выполняется соотношение x y.

Гомотетичные предпочтения называют так, поскольку геометрически кривые безразличия гомотетичны относительно начала координат. Рис. 2.11 иллюстрирует понятие гомотетичных предпочтений. Наборы x00 и y00 , лежащие на кривой безразличия I00 , получаются из наборов

x0 и y0 , лежащих на кривой безразличия I0 , умножением на одно и то же положительное число t (x00 = tx0 и y00 = ty0 ).

29Доказательство этого факта см. в K. J. Arrow and A. C. Enthoven: Quasi-Concave Programming, Econometrica 29 (1961): 779–800.

x2

x00

x0

y00

y0 I00

I0

x1

Рис. 2.11. Монотонные гомотетичные предпочтения

Опираясь на схему доказательства существования функции полезности, представляющей строго монотонные предпочтения, приведенного в предшествующем параграфе (см. Теорему 10), легко показать, что для строго монотонных и гомотетичных предпочтений существует положительно однородная функция полезности, представляющая эти предпочтения. Особенностью положительно однородной функции полезности является то, что предельная норма замены для любой пары товаров остается неизменной на луче tx. Это полезное свойство эквивалентно тому, что кривые Энгеля30 являются лучами, выходящими из начала координат. Кроме того, при выполнении этого свойства, свойств локальной ненасыщаемости, непрерывности и выпуклости, неоклассические предпочтения допускают представление вогнутой функцией полезности31.

В теории отраслевых рынков и других областях микроэкономики важную роль играют предпочтения, обладающие свойством квазилинейности.

Определение 14:

Предпочтения называются квазилинейными по l-му благу, если

• для каждого положительного t из x X следует x + tel X ;

• для каждого положительного t и x, y X из x y следует x + tel y + tel .

x2

x1

Рис. 2.12. Квазилинейные предпочтения

Предпочтения, обладающие данным свойством, допускают представление функцией полезности вида u˜(x) = u(x−l) + axl . Эта функциональная форма задает такую систему функций

30См. Определение 28 на с. 92.

31Подробнее см. J. T. Rader: Theory of Microeconomics, New York: Academic Press, 1972, pp. 166–167.