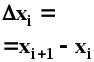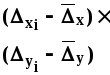Корреляция отклонений от средних отклонений

Год
1977	108	11,8
1978	81	15,4	-27	+3,6	-32,8	+2,86	-93,8	1075,8	8,2
1979	106	13,0	+25	-2,4	+19,2	-3,14	-60,3	368,6	9,9
1980	124	13,9	+18	+0,9	+12,2	+0,16	+2,0	148,8	0,0
1981	103	15,1	-21	+1,2	-26,8	+0,46	-12,3	718,2	0,2
1982	106	19,6	+3	+4,5	-2,8	+3,76	-10,5	7,8	14,1
1983	149	16,2	+43	-3,4	+37,2	-4,14	-154,0	1383,8	17,1
1984	148	17,2	-1	+1,0	-6,8	+0,26	-1,8	46,2	0,1
1985	102	24,0	-46	+6,8	-51,8	+6,06	-313,9	2683,2	36,7
1986	130	22,4	+28	-1,6	+22,2	-2,34	-51,9	492,8	5,5
1987	80	32,3	-50	+9,9	-55,8	+9,16	-511,1	3113,6	83,9
1988	139	24,7	+59	-7,6	+53,2	-8,34	-443,7	2830,2	69,6
1989	183	21,4	+44	-3,3	+38,2	-4,04	-154,3	1459,2	16,3
Σ	1559	247,0	+75	+9,6	-	-	-1805,6	14328,2	261,6

Эти методы лучше применять только при явном преобладании колеблемости над тенденцией изменения за единицу времени, т.е. при малом показателе К для линейных трендов или малых аналогичных показателях для других типов трендов (см. разд. 8.3).

9.5. Корреляция с учетом лага и циклов

Среди природных и общественных явлений нередко встреча­ются такие, которые связаны между собой не в одном и том же периоде времени, а с некоторым запозданием - по-английски - lag, откуда пошел термин лаг. Например, капиталовложения в создание машиностроительного, автомобильного завода отра­зятся в росте объема производства не в том году, когда они про­изведены, а через два-три и более лет, капиталовложения в строительство крупной гидроэлектростанции - через 6-8 лет. При наличии лага в реальной связи изучаемых явлений измерять кор­реляцию факторного признака с результативным нужно, конеч­но, не по одновременным уровням, а с учетом лага. Например, отклонение от тренда капиталовложений скажется на отклоне­нии от тренда выпуска продукции через k лет. Значит, измерять корреляцию нужно через произведения .

Методика корреляции с учетом лага делится на два под­вида:

А. Случай, когда величина лага известна заранее.

Б. Случай, когда саму величину лага следует определить на основе измерения корреляции.

Вначале рассмотрим случай А. Например, на сельско­хозяйственном предприятии принят и длительное время дей­ствует следующий севооборот: после трех лет многолетних трав участок занимает пропашная культура: картофель, бобовые, овощи, под которые вносится большая доза органических удоб­рений, а в следующем году на участке высевают зерновые куль­туры. Необходимо измерить связь между дозой органических удобрений, внесенных под пропашные культуры, и урожайнос­тью зерновых. В данном случае k = 1 году, расчет корреляции приведен в табл. 9.5.Таблица 9.5

Корреляция с лагом в 1 год

Год	Доза, т/га,	Урожайность, Ц/га,	Тренд	Отклоне­ние,	-= =	* *
1987	45	13,0	15,0	-2,0	+4	+9,6	16	4,00	15,0
1988	36	18,0	15,6	+2,4	-5	-1,5	25	5,76	16,5
1989	47	16,5	16,2	+0,3	+6	-10,2	36	0,09	15,0
1990	33	15,1	16,8	-1,7	-8	+23,2	64	2,89	18,2
1991	42	14,5	17,4	-2,9	+1	0,0	1	8,41	15,6
1992	51	18,0	18,0	0,0	+10	+38,0	100	0,00	18,2
1993	36	22,4	18,6	+3,8	-5	+2,5	25	14,44	20,9
1994	42	18,7	19,2	-0,5	+1	+3,2	1	0,25	18,0
1995	35	23,0	19,8	+3,2	-6	+3,6	36	10,24	20,0
1996	40	19,8	20,4	-0,6	-1	+2,0	1	0,36	19,0
1997	44	19,0	21,0	-2,0	+3		9	4,00	20,8
Σ	451	198,0	198,0	0,0	0	+70,4	314	50,44	197,2

При этом будем считать, что тренд дозы внесенных органических удобрений отсутствует или несуще­ствен.

Средняя доза удобрений: =451:11 = 41 т/га.

Тренд урожайности: = 18,0 + 0,6 • ;t = 0 в 1992 г.

Коэффициент корреляции с учетом лага в 1 год имеет вид:

Связь колебаний дозы удобрений под предшественник зер­новых с колебаниями их урожайности на следующий год оказа­лась средней силы: за счет этой связи объясняется 35% всей колеблемости урожайности.

ний под пропашные культуры в среднем давала прибавку уро­жайности зерновых на следующий год 0,23 ц/га.

Уравнение регрессии имеет вид: 0,2308, свобод­ного члена это уравнение не имеет, так как средние отклонения от тренда и от средней дозы равны нулю. Рассчитанные по этой формуле значения урожайности, т.е. трендовые значения даны в последней графе табл. 9.5.

Обратите внимание на особенности сумм произведений и сумм квадратов в формулах коэффициента корреляции и коэф­фициента регрессии: в сравнении с суммами при корреляции отклонений без лага число слагаемых на единицу меньше: в од­ной из сумм - от конца, в других - от начала. Если же лаг велик, то число слагаемых сильно сократится, а значит, корреляция станет менее надежной: ведь оценка надежности коэффициен­тов должна рассчитываться в этом случае не по общему числу членов первичного ряда, а исходя из числа реально участвую­щих в работе коэффициентов. При лаге в 5 лет это число соста­вит (п – 5), а затем еще надо исключить две степени свободы при парной корреляции. Откуда следует еще один вывод: при ко­ротком исходном ряде (рядах) и большом лаге показатели связи колебаний признаков будут заведомо ненадежны.

Теперь рассмотрим случай Б, когда величина лага зара­нее неизвестна и должна быть определена с помощью корреляционного анализа. Имея в данном случае дело с недостаточно изученными явлениями, назовем коррелируемые признаки «икс» и «игрек». Если их временные ряды достаточно велики, нахо­дим тренды и, отклонения отдельных уровней от трендов , и начинаем вычислять корреляцию между ними: снача­ла без лага, затем с лагом в один период, с лагом в два периода и т.д. Получается серия (или вектор) коэффициентов корреляции между колебаниями признаков х и у с возрастающим лагом. Гра­фическое изображение этого вектора принято называть коррелограммой.

Коррелограмма может иметь два вида:

• коэффициенты до какого-то сдвига растут, а затем убыва­ют до незначимо отличных от нуля величин, тогда лаг считает­ся равным тому сдвигу отклонений, при котором коэффициент корреляции по модулю максимален;

• коэффициенты поочередно растут и убывают, образуя цик­лы или квазициклы, т.е. локальные максимумы наблюдаются, скажем, то через три года, то через четыре года. Лагом в этом случае считается средний промежуток времени между локаль­ными максимумами коэффициентов корреляции, между откло­нениями от трендов.

Рассчитываем коэффициенты корреляции отклонений от тренда, начиная с нулевого лага (табл. 9.6):

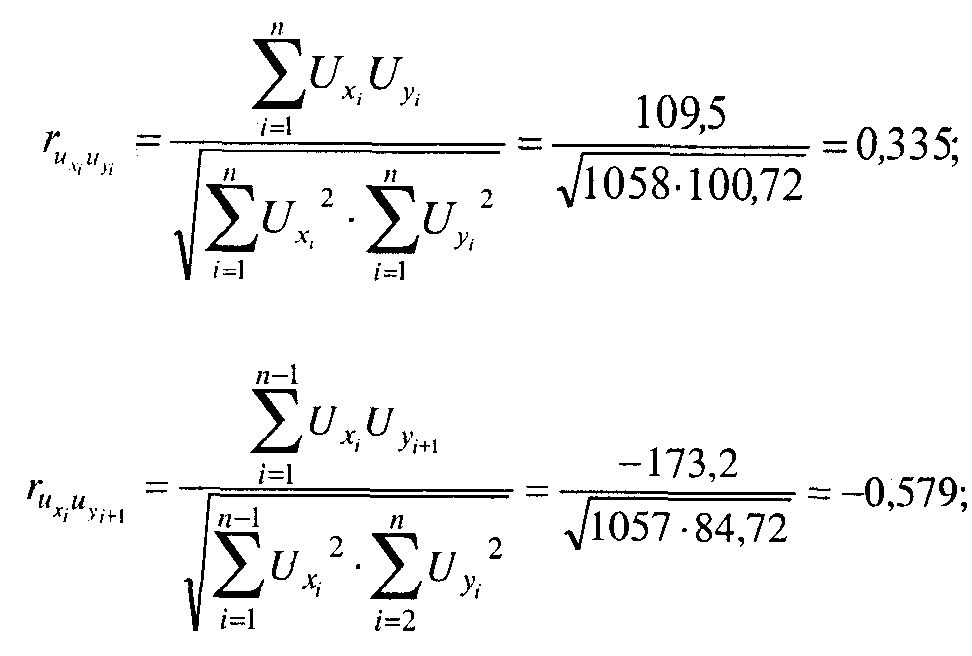
Таблица 9.6