9.2. Агрегирование трендов и колебаний по совокупности объектов

9.2.1. Тренды объемных признаков

Рассмотрим проблему соотношения тренда и колеблемос­ти по совокупности объектов (например, тренда и колеблемос­ти валового сбора по району в целом) и соотношения трендов и колебаний того же показателя в каждой единице совокупности (по каждому хозяйству). Иначе говоря, в отличие от мульти­пликативной системы, представленной в разд. 9.1, рассмотрим аддитивную систему.

Эта проблема в нашей статистической литературе рассмат­ривалась очень кратко для частного случая И. Поповой [13, с. 57-61] и в общем случае В.Н. Афанасьевым [2].

Сначала обсудим проблему агрегирования трендов объем­ных признаков, например валового сбора. Очевидно, что каж­дый уровень признака по совокупности хозяйств равен сумме валовых сборов всех единиц этой совокупности:

Средний уровень за ряд лет по совокупности - свободный член линейного тренда - равен, следовательно, сумме свобод­ных членов линейных трендов валового сбора по всем едини­цам совокупности.

Далее покажем, из чего складывается среднегодовой при­рост валового сбора по совокупности:

где j - номера единиц совокупности.

Следовательно, средний абсолютный прирост тренда по со­вокупности в целом равен сумме средних абсолютных прирос­тов по всем единицам совокупности. Таким образом, теорема агрегирования для линейных трендов доказана.

Для параболических трендов средний абсолютный прирост совпадает с таковым для прямой, доказательство уже имеется. Система уравнений МНК для других параметров параболы по совокупности в целом имеет вид:

Подставляя в правые части 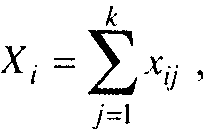имеем

Решая эту систему уравнений, получаем:

Вторая скобка не содержит величины признака и в рас­смотрении не нуждается. Первая скобка преобразуется в следу­ющее выражение:

что после деления каждого из у слагаемых на вторую скобку дает

т.е. квадратический параметр параболы по совокупности в целом равен сумме квадратических параметров по всем еди­ницам совокупности. Свободный член параболического тренда по совокупности А вычисляем после нахождения С по формуле

Таким образом, свободный член параболы по совокупнос­ти в целом равен сумме свободных членов уравнений трендов по всем единицам совокупности. Доказана и теорема сложения для параболических трендов. Разумеется, если по части единиц совокупности тренды линейные, а по другим единицам - пара­болические, то и в этом случае соблюдается правило суммиро­вания трендов. Прямую можно считать частным случаем параболы при пулевом ускорении.

В случае экспоненциальных трендов по каждой единице со­вокупности тренд по совокупности в целом также является экспонентой, коэффициент роста которой k является не постоянной, а переменной величиной, в каждом периоде равной средней арифметической взвешенной из индивидуальных темпов по величине уровней предыдущего периода. С течением времени общий темп роста по совокупности асимптотически прибли­жается к величине темпа роста, являющегося наибольшим из всех индивидуальных темпов, так как уровень признака у еди­ницы совокупности с наибольшим темпом роста со временем становится преобладающим в совокупности, его доля стремит­ся к единице. Разумеется, теорема сложения трендов к экспо­нентам неприменима. Она заменяется теоремой усреднения трендов, которую здесь излагать не будем.