Определение отклонений логарифмов уровней от логарифмов тренда

Год	ln	ln	Отклонения
1950	7,835	7,849	-0,014	0,000196	-2,5	6,25
1960	8,026	8,027	-0,001	0,000001	-1,5	2,25
1970	8,223	8,206	+0,017	0,000289	-0,5	0,25
1980	8,396	8,384	+0,012	0,000144	0,5	0.25
1990	8,564	8.562	+0,002	0,000004	1,5	2,25
2000*	8,726	8,741	-0,015	0,000225	2,5	6,25
Σ	49,770	49,770	0	0,000859	0,0	17,50
* Оценка

Средняя ошибка логарифма коэффициента изменения:

Табличный критерий Стьюдента при четырех степенях сво­боды и значимости 0,01 равен 4,60. Полученное значение кри­терия много больше табличного, так что вероятность нулевой гипотезы можно считать равной нулю, а рост населения Земли -достоверным. Понятно, что столь очевидное явление и не тре­бовало проверки, пример приведен для показа методики надеж­ности экспоненциального тренда, а не для проверки самого факта роста населения, как это имело место в примере с ростом среднегодовой температуры.

Для кривых, не имеющих постоянного основного парамет­ра, вышеизложенный метод проверки надежности неприменим. В таких случаях можно, во-первых, проверять сам факт нали­чия какого-либо тренда путем сравнения средних уровней за первую и за вторую половины периода, во-вторых, с помощью обычной методики проверки надежности различия двух сред­них величин в теории выборочного метода. Если различие сред­них уровней в более ранний период и в более поздний период надежно (нулевая гипотеза отвергается), значит, тренд существу­ет. А о форме уравнения тренда судим по тем методикам и по­казателям, которые изложены в гл. 5.

7.2. Доверительные границы тренда

Если уравнение тренда рассматривается как выборочное, имеющее ошибки репрезентативности своих параметров, то мож­но рассчитать доверительные границы, внутри которых с задан­ной, достаточно большой вероятностью, проходит линия тренда в генеральной совокупности. Рассмотрим этот случай на приме­ре простейшего, линейного тренда. Оба его параметра - свобод­ный член а и среднее изменение за единицу времени b имеют ошибки репрезентативности выборочных оценок. Свободный член уравнения тренда - это выборочная средняя величина уров­ней временного ряда, средняя ошибка репрезентативности кото­ рой определяется по формуле

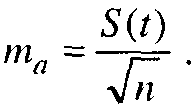
Средняя ошибка репрезентативности параметра b, как упоминалось выше, равна:

Свободный член уравнения линейного тренда и среднее из­менение за единицу времени - величины независимые, а следо­вательно, согласно теореме сложения дисперсий независимых величин, дисперсия их суммы равна сумме дисперсий слагае­мых, а среднее квадратическое отклонение (средняя ошибка) - корню квадратному из суммы дисперсий, т.е. из суммы квадра­тов ошибок т²a и т²b. Однако мы рассматриваем ошибку не в статике, а в динамике. Средняя ошибка положения линии трен­да за счет ошибки свободного члена - это константа для любой точки линии тренда, а средняя ошибка изменения уровня трен­да за счет ошибки параметра b - это величина переменная, ибо в разных точках линии тренда его уровень равен а + b, и ошибка параметра b возрастет в раз по сравнению с ошибкой в точке, где= 1. Следовательно, ошибка линии тренда минимальна в середине базы его расчета - в середине временного ряда. В этой точке, гдеt = 0, средняя ошибка положения линии тренда рав­на ошибке его свободного члена, т.е. S(t)/ , а в любой иной точке тренда его средняя ошибка вычисляется по формуле

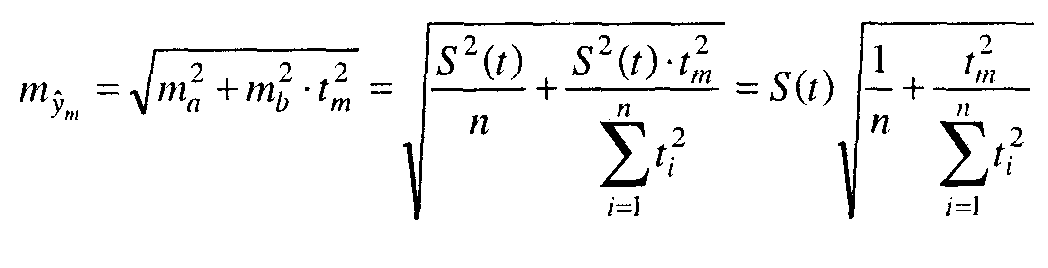
- для однократного выравнивания и при = 0 в середине ряда. При нумерации периодов времени от начала ряда вместов формулу следует подставить величину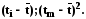

При многократном скользящем определении параметра b второе слагаемое подкоренного выражения примет вид:

где п - длина одной базы расчета тренда;

l - число баз.

Рассчитаем среднюю ошибку тренда среднегодовой темпе­ратуры воздуха в Санкт-Петербурге:

Для середины ряда - 1977 г. - средняя ошибка тренда соста­вила:

А для крайних уровней-1957г. и 1997г.-

Таким образом, ошибка тренда возрастает от середины базы его расчета (середина ряда) к его краям, образуя конусообраз­ную зону вероятных значений генерального тренда.

Если эту зону мы хотим определить с достаточно большой вероятностью, то среднюю ошибку следует умножить на вели­чину t-критерия Стьюдента для соответствующей вероятности. Границы доверительной зоны тренда среднегодовой темпера­туры с вероятностью 0,95 изображены на рис. 7.1.

Чем сильнее колеблемость уровней и чем меньше база рас­чета тренда, тем шире доверительная зона генерального трен­да и тем быстрее она расширяется от середины ряда к его концам. Зона для параболического тренда расширяется при этом гораздо сильнее, чем для линейного тренда.

Рис. 7.1. Доверительные границы генерального тренда среднегодовой температуры воздуха в Санкт-Петербурге

——— средний тренд

——— границы тренда с вероятностью 0,95