10.4.2. Модель трепда годовых уровней

и тригонометрического уравнения сезонности

В разд. 6.3 приведен расчет модели сезонных колебаний ме­сячных надоев молока на среднюю корову в форме тригоно­метрического уравнения первой гармоники ряда Фурье. Если продолжить анализ за 9 лет, получим модель:

Yj = 316,7 + 45,4 sintj -83 cost,,

где у, - надой молока зау-й месяц;

316,7- средний месячный надой в среднем году базы расчета тренда 1989-1997 гг., т.е. в 1993 г.;

t. - номер месяца года, начиная от января, для которого t. = О, умноженный на 30 градусов дуги (360° : 12).

209

Имеем также меру случайной колеблемости:

Тренд имеет вид:

Чтобы построить по этим данным объединенную модель тренда и сезонности, необходимо учесть, что коэффициенты при синусе и косинусе зависят от величины свободного члена урав­нения - среднего за данный год месячного надоя. Следователь­но, эти коэффициенты каждый год необходимо корректировать на изменение по тренду среднемесячного надоя, т.е. для года с номером i они примут вид:

Сама же объединенная модель месячных надоев будет иметь следующее выражение:

Рассчитаем по этой модели прогноз (точечный) надоя на корову в апреле 1999 г.:

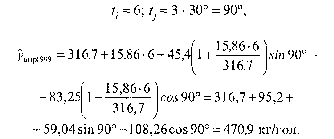
С учетом того, что средняя колеблемость не будет возрас­тать пропорционально надою год от года, имеем среднюю ошиб­ку прогноза:

210

С вероятностью 0,95 продуктивность коров в хозяйстве в апреле 1999 г. составит при семи степенях свободы:

470,9 ± 2,36 • 14,4, или от 436,9 до 504,9 кг/гол.

Рассчитаем по той же модели прогноз надоя молока на сред­нюю корову на ноябрь 2000 г.:

Точечный прогноз:

Средняя ошибка прогноза:

С вероятностью 0,95 средний надой молока на корову в но­ябре 2000 г.составит:

302,4 ± 2,36 • 15,3, или от 266,3 до 338,5 кг/гол.

Если же принять гипотезу о росте случайных колебаний по абсолютной величине пропорционально росту среднего надоя, то средняя ошибка получит для ноября 2000 г. вид:

т.е. больше на треть, чем без учета тенденции роста абсолютно­го показателя случайной колеблемости. Соответственно станут шире и доверительные интервалы прогнозов. Для проверки су­ществования или отсутствия трепда случайной колеблемости необходим достаточно длительный временной ряд, а это, как уже отмечалось в разд. 6.4, не всегда имеется в условиях зада­чи. Если такая возможность есть, следует для расчета ошибок прогноза учесть тенденцию случайной колеблемости.

211

10.5. Прогнозирование комплекса жестко взаимосвязанных признаков

В данном разделе на основе доказанных в гл. 9 свойств трен-дов и колебаний в системе жестко взаимосвязанных признаков рассматриваются проблемы прогнозирования такой системы, как, например, площадь посева, урожайность и валовой сбор сельскохозяйственных культур или численность работников предприятия, производительность их труда, выпуск продукции.

В разд. 9.1 было доказано, что при наличии колеблемости признаков-сомножителей тренд признака-произведения содер­жит дополнительные случайные элементы, зависящие от сочета­ния разнораспределенных по времени колебаний сомножителей и корреляции между ними. Из этого положения вытекает, что предпочтительнее прогнозировать уровни признаков-сомножи­телей, а их произведение даст прогноз признака-произведения. Такой прогноз будет меньше зависеть от случайного распреде­ления отклонений уровней в отдельные годы, чем прогноз по тренду признака-произведения.

Конечно, не следует забывать, что мы имеем дело со стати­стической закономерностью: не в каждой отдельной задаче про­гнозирования, а лишь как математическое ожидание или средняя величина ошибок прогнозов по множеству задач про­явится теоретическое преимущество прогнозов по трендам со­множителей. В отдельном случае ошибка прогноза по тренду произведения может быть и меньше, ошибка может быть слу­чайно вообще равна нулю. Но решать проблему выбора мето­дики необходимо исходя из доказанного преимущества прогноза по произведению трендов сомножителей.

По данным табл. 9.1 вычислим прогноз валового сбора зер­на на период с номером 6 от середины базы расчета трендов. Алгоритм расчета точечного прогноза валового сбора может иметь два варианта:

а) прогнозируем площадь, затем урожайность по их трен-дам, после чего перемножаем прогнозы:

212

б) перемножаем тренды площади и урожайности и на осно­ве полученной параболы вычисляем прогноз валового сбора:

Средняя ошибка выборочной оценки или прогноза произ­ведения двух переменных вычисляется по формулам:

(10.11)

если признаки П и у независимы друг от друга;

(10.12)

если признаки П и у в динамике коррелированы.

Здесь w//^ и niy^ - средние ошибки прогнозов признаков-сомножителей па период t^; r'„ - коэффициент корреляции между признаками-сомножителями в динамике, вычисление ко­торого описано в разд. 9.4, т.е. коэффициент корреляции от­клонений от тревдов, ранее уже рассчитанный выше: т-'^ == = -0,326. Средние ошибки прогнозов отдельного признака рассмотрены в разд. 10.3.2. Имеем:

Подставляя в формулу средней ошибки прогноза валового сбора с учетом корреляции колебаний площади с урожайнос­тью, имеем:

С вероятностью 0,9 ((-критерий Стыодепта при семи степе­нях свободы равен 1,95) доверительный интервал валового сбо­ра составит:

213

5250 ± 1,95 • 836,2, или от 3619 до 6881 ц.

Широкий интервал прогноза, во-первых, связан с коротко! базой расчета трендов, во-вторых, с довольно значительной ко леблемостыо урожайности.