39,48 ± 2,09 • 1,06, Или от 37,26 до 41,70 млн т. И после 1995 г. Имеем фактический среднегодовой сбор:

(38,9 + 46,2 + 43,5 + 32,1 + 30,1) : 5 = 38,16 млн т.

Как видим, фактический среднегодовой валовой сбор нахо­дится в границах всех постепенно сужающихся доверительных интервалов прогноза. Ретроспективная проверка методики про­гноза показала ее состоятельность, несмотря на явно кризисные годы сельского хозяйства в РФ.

10.3.4. Расчет страхового запаса для преодоления риска отклонения от трепда

Доверительные интервалы прогноза могут служить основа­нием для расчета рисков больших отклонений от тренда и стра­хового запаса для преодоления этого риска. В предыдущем разделе вычислены границы доверительного интервала прогноза валового сбора пшеницы в России на 1991-1995 гг.: среднего­довой валовой сбор ожидался с вероятностью 0,95 в границах

206

от 27,62 до 48,14 млн т. Это означает, что при близком к нор­мальному закону распределения отклонений от тренда вероят­ность того, что валовой сбор окажется в среднем за год ниже 27,62 млн т, равна: (1 - 0,95) : 2 = 0,025, или риск 2,5%. Однако если для нормального обеспечения населения России продо­вольствием необходимо 30 млн т пшеницы в год, то вероятность риска будет больше. Для ее определения следует вычислить кратность отклонения 30 млн т от точечного прогноза тренда 37,88 млн т в единицах S(t), т.е. 7,88 :7,18= 1,097== 1,10. Веро­ятность того, что отклонение от тренда превысит -1,15(0 есть (1 -F(l,l): 2= (1-0,714): 2= 0,143, или 14,3%, Такой высокий риск неприемлем, и для его перекрытия и доведения до прием­лемого уровня в 2,5% необходимо иметь страховой запас зерна пшеницы 30 - 27,62 == 2,38 млн т на год, или 2,38 • 5 = 11,9 млн т на все пятилетие. Либо иметь резерв валюты и договора о по­ставке пшеницы из-за рубежа на сумму стоимости этих 11,9 млн т плюс стоимость перевозки. Как видим, расчет доверительных границ валового сбора и на отдельный год, и на большие сро­ки может иметь важное народнохозяйственное значение. По вер­хней границе доверительного интервала можно рассчитать вероятность иного, не столь драматического риска: риск пере­производства, нехватки емкостей для хранения зерна, сниже­ния цены на рынке ниже уровня рентабельности.

10.4. Прогнозирование по модели тренда и сезонных колебаний

В гл. 6 были рассмотрены две модели сезонных колебаний:

с помощью средних индексов сезонности каждого месяца за ряд лет и с помощью ряда Фурье, или тригонометрических функ­ций. Прогнозирование по каждой из этих моделей с учетом трен­да либо месячных уровней, либо среднегодовых уровней излагается в данном разделе.

207

10.4.1. Модель трспда месячных уровней и средних индексов сезонности

Имеем тренд месячных уровней затрат труда в сельскохозяй­ственном предприятии за 1995-1997 гг. (тыс. ч) у^ = 60,03+1,085?,, t = 0 в июле 1996 г., и вектор средних индексов сезонности для каждого месяца:

Месяц 'сеч	Месяц 'сез.	Месяц 'сез;
Январь 0,433 Февраль 0,394 Март 0,517 Апрель 0,777	Май 1,617 Июнь 1,481 Июль 1,219 Август 1,680	Сентябрь 1,617 Октябрь 1,206 Ноябрь 0,734 Декабрь 0,471

Среднее квадратическое отклонение фактических уровней от расчетных по тренду с учетом сезонных колебаний, т.е. мера случайной колеблемости S(f\, равно 4,08 тыс. ч.

Модель, учитывающая тренд и сезонность, имеет вид:

Подстановкой в эту модель /-го номера месяца от середины базы и соответствующего этому месяцу у-го номера в году по­лучаем точечный прогноз затрат труда в ij-м месяце. Напри­мер, для апреля 1999 г.:

Средняя ошибка прогноза месячного уровня, вызванная на­личием случайной колеблемости, вычисляется по ранее приве­денным в разд. 10.3.2 формулам. Для апреля 1999 г.:

208

Доверительные границы затрат труда в апреле 1999 г. со­ставят с вероятностью 0,95 (/-критерий Стьюдента t " 2):

74,46 ± 2 • 4,63, или от 65,20 до 83,72 тыс. ч. Для декабря 1998 г.:

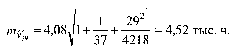
Доверительные границы с вероятностью 0,9 составят:

43,09 ± 1,65 • 4,52, или от 35,63 до 50,55 тыс. ч.

Без учета сезонных колебаний прогноз был бы лишен всякого смысла, так как среднее квадратическое отклонение за счет се­зонных колебаний равно 30,8, т.е. в 7,5 раза больше, чем случай­ная колеблемость, и ошибки прогнозов были бы во столько же раз больше, а доверительные интервалы - от нуля и до 100 с лиш­ним. Такой «прогноз» можно сделать и без научных методов.

Следует, однако, подчеркнуть, что изложенная выше мето­дика не лишена дискуссионных моментов: как, например, раз­делить степени свободы между сезонной колеблемостью и случайной? Измерять ли силу сезонной колеблемости по первич­ному ряду через j); • 1^ - у, или в относительном выражении че­рез средние индексы сезонности (их отклонения от 100% или от единицы)?