10.3.3. Прогноз доверительного интервала для среднего уровня за ряд периодов

Предметом прогнозирования может быть не только уровень отдельного года или месяца, но и средний уровень за ряд перио­дов (моментов). Рассмотрим, что в этом случае можно считать точечным прогнозом и какова формула средней ошибки прогно­за среднего уровня.

При линейной форме тренда приросты уровней или их со­кращения - постоянная величина. В этом случае средняя вели-

202

чипа прогнозируемых уровней равна уровню на середину про­гнозируемого периода, например, при прогнозе среднегодово­го уровня на 1998-2002 гг. за точечный прогноз следует взять прогнозируемый на 2000 г. уровень. Он равен среднему уров­ню за 1998-2002 гг., так как

Если тренд нелинейный, то среднюю величину прогнозиру­емых уровней за т лет следует вычислять как простую арифме­тическую величину после вычисления точечных прогнозов на каждый из т лет. При экспоненциальной форме тренда для рас­чета среднего уровня за т лет можно приближенно использо­вать ту же формулу, что и для линейного тренда, только если средний темп роста (снижения) близок к единице, отличается, например, не более чем на ±0,05 о т 1. В таких случаях геомет­рическая средняя (уровень середины периода т) мало отлича­ется от арифметической средней.

Средняя ошибка прогноза тренда изменяется даже для ли­нейного тренда неравномерно, поэтому в общем случае она не равна ошибке прогноза тренда для среднего периода прогно­зируемого отрезка времени. Но для линейного тренда разли­чие невелико, так что допустимо пользоваться расчетом ошибки прогноза тренда на середину прогнозируемого периода (пер­вая составляющая), т.е. для t ,„, для которого при линейном *+-^-

тренде вычисляется и точечный прогноз уровня. Вторая состав­ляющая ошибки прогноза среднего уровня на т периодов, т.е. среднее квадратическое отклонение от тренда для т периодов,

согласно теории выборочного метода, уменьшается в ^[т раз. Итак, получаем общую формулу средней ошибки прогноза сред­него уровня для отрезка т единичных периодов после периода с номером ?д. от середины базы расчета тренда:

203

(10.9)

Если тренд S(f) и его прогноз не вычислялся или несуще­ствен, то имеем:

(10.10)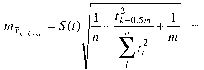

для однократного выравнивания и соответственно измененную формулу - для многократного расчета параметра линейного тренда, которую легко выведут внимательные читатели сами.

Для нелинейных трендов ошибку тренда для прогнозируе­мого отрезка в т периодов следует вычислять как среднюю арифметическую величину из всех индивидуальных ошибок прогнозов тренда для каждого из т периодов с номерами от

от середины базы расчета тренда. Затем к квадрату

ошибки тренда добавляете?

и вычисляется квадратный

корень из суммы подкоренных дробей.

Например, поданным за 1970-1990 гг. тренд i^i-ioisoro сбо­

ра пшеницы в России имел вид:

в 1980г.

Рассчитаем по этому тренду прогноз среднегодового вало­вого сбора на 1991-1995 гг. и его доверительные границы без учета тренда колеблемости при S(f) =7,18 млн т. За точечный берем прогноз тренда на 1993 г.:

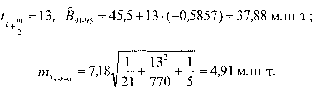
204

С вероятностью 0,95 доверительный интервал прогноза среднегодового валового сбора зерна пшеницы в России при условии сохранения до 1995 г. прежнего тренда составил: 37,88 + + 2,09 • 4,91, или от 27,62 до 48,14 млн т. Широкий интервал вызван значительной силой колеблемости и требованием вы­сокой надежности прогноза.

С учетом тенденции колебаний к их уменьшению ошибка прогноза была бы меньше, но для дальнейшего изложения это приведет к чрезмерному усложнению расчетов'.

Рассмотрим, как меняются прогноз и его ошибка при по­степенном получении фактических уровней прогнозируемого отрезка времени, т.е. после получения в нашем примере дан­ных за 1991 и 1992 гг. и т.д. Ясно, что при каждом поступле­нии взамен прогнозируемой величины фактического уровня должна уменьшаться и ошибка прогноза среднего уровня на пятилетие и при замене последнего прогноза на 1995 г. на фак­тический уровень ошибка становится нулем. Рассмотрим этот процесс подробно. Пришел 1991 г., и получен его валовой сбор 38,9 млн т. Теперь среднегодовой уровень на 1991-1995 гг. равен сумме 38,9 + четыре прогноза на 1992-1995 гг., делен­ной на пять. Если исходить из того, что уравнение тренда не будет ежегодно пересматриваться, имеем:

Средняя ошибка прогноза среднегодового сбора равна сум­ме нуля (для 1991 г.) и четырех ошибок для 1992-1995 гг., де­ленной на пять:

(О + 4,73 + 4,91 + 5,09 + 5,28) : 5 = 4,00.

Соответственно уменьшится ширина доверительного интер­вала прогноза. Прошел 1992 г., валовой сбор этого года равен 46,2 млн т. Теперь точечный прогноз среднегодового уровня 1991-1995 гг. составит: (38,9 + 46,2 + 37,9 + 37,3 + 36,7) : 5 = = 39,4 млн т. Средняя ошибка этого прогноза равна: щ = (0 + + 0 + 4,91 + 5,09 + 5,28): 5 = 3,06, доверительный интервал с вероятностью 0,95 равен: 39,4 ± 2,09 • 3,06, или от 33,0 до

' Такой расчет мог бы стать темой дипломного исследования по статистике.

205

45,8 млн т. После 1993 г., валовой сбор в котором равен факти­чески 43,5 млн т, имеем:

точечный прогноз

(38,9 + 46,2 + 43,5 + 37,3 + 36,7) : 5 = 40,52;

среднюю ошибку

(О + 0 + 0 + 5,09 + 5,28): 5 = 2,07;

доверительный интервал прогноза среднегодового валово­го сбора

40,52 ± 2,09 • 2,07, или от 36,19 до 44,85 млн т.

После 1994 г. с его фактическим валовым сбором 32,1 млн т имеем:

точечный прогноз

• (38,9 + 46,2 + 43,5 + 32,1 + 36,7): 5 = 39,48;

среднюю ошибку

(О+0+0+0+5,28): 5= 1,06;

доверительный интервал