10.3.2. Прогноз доверительного интервала для уровня отдельного периода (момента)

Неопределенность прогноза уровня отдельного периода складывается из двух элементов: ошибки линии тренда для про­гнозируемого периода и колебаний уровня около тренда. Пер­вый элемент рассмотрен в предыдущем разделе. Колеблемость отдельных уровней относительно линии тренда измеряется сред­ним квадратическим отклонением S(t). Однако необходимо от­ветить на вопрос: допустимо ли переносить значение этой величины, полученное за период-базу, на прогнозируемый пе­риод? Теоретически могут иметь место изменения величины ко­лебаний и в сторону их роста при тенденции роста уровней и постоянстве факторов колеблемости (постоянном коэффициен­те колеблемости), и в сторону сокращения абсолютной величи­ны колебаний при их сознательном подавлении, например колебаний урожайности при прогрессе агротехники, мелиора­ции земель.

Таким образом, в расчет ошибки прогноза и тренда, но осо­бенно ожидаемого отдельного уровня в прогнозируемом пери­оде, следует взять ожидаемое значение показателя колеблемости

для этого же прогнозируемого периода S(t\, расчет которого приведен в разд. 6.4. Читатель, склонный к математическому

199

образу мышления, тут же может заметить, что тренд колебле­мости и ее прогноз на будущее - опять же неабсолютная исти­на, трепд имеет свою ошибку, которую также нужно учесть,

используя в прогнозе уровня не S(t),,, а доверительный интер­вал 5(?)^ +t^ -m„ и т.д. На эти теоретически верные рассуж­дения следует ответить тем, что ограниченная точность и надежность исходных уровней временного ряда приводят к тому, что дальнейшие итеративные шаги по расчету ошибки ошибок прогноза и т.д. становятся всего лишь математическим упраж­нением, не улучшающим точность прогноза на практике. В свя­зи с этим при расчете средней ошибки прогноза уровней ряда мы рекомендуем использовать только точечный прогноз силы

Wk+tc. •'"§(,),

колебаний S(t)i^, если тренд колеблемости надежно установлен (см. разд. 7.3), или величину S(t) по базе прогноза, если измене­ние этого показателя со временем не установлено надежно.

Кроме этого необходимо быть осторожным с линейными трендами уменьшения колеблемости. Пока это сокращение не­значительно и значение S(t) далеко от нуля, использовать про­гноз по линейному тренду можно, но ведь при дальнейшем снижении по прямой показатель колеблемости когда-то ста­нет равным нулю, чего на самом деле быть не может. Колеб­лемость - такой же незыблемый закон природы, как и вариация признаков в пространстве: она не может быть уничтожена. Для прогнозов показателей колеблемости на более далекую перс­пективу при тенденции ее сокращения следует применять ги­перболическую форму тренда.

Определив величину показателя колеблемости для прогно­зируемого периода, подставляем этот показатель вместе с ошиб­кой прогноза тренда в единую формулу средней ошибки прогноза конкретного отдельного уровня опираясь на прави­ло сложения независимых дисперсий:

(10.5)

Эта формула является общей для любых типов линии трен­да. Для каждого типа различны первые слагаемые - ошибки

200

тренда на период ^. Для линейного тремда при однократном его расчете, используя формулы (10.1) и (10.3), имеем:

(10.6)

Эта формула должна применяться, если приведен расчет ве­личины S(l)^ на прогнозируемый период, так как в этом случае в первых двух дробях в числитель входит величина S(l) за пери­од-базу, а третье слагаемое подкоренного выражения - это про­гнозируемая величина колеблемости на прогнозный период. Таким образом, «вынести за знак корня величину» S(t) нельзя, так как они под корнем различные.

Если же на период прогноза принята та же величина показа­теля колеблемости, как и за период-базу расчета тренда, то эта величина выносится из-под корня, тогда имеем:

(10.7)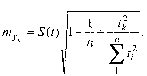

Именно данная формула приводится обычно в учебниках. Соответственно при многократном расчете среднегодового прироста Ь получаем формулу

(10.8)

Значения обозначений те же, что в формулах (10.1 и 10.3).

Для всех других типов тренда средняя ошибка отдельного уровня вычисляется по общей формуле.

По ранее рассмотренным примерам имеем.

1. Прогноз численности занятых в народном хозяйстве в РФ на 1998 г. без учета тренда колеблемости:

201

С вероятностью 0,95 численность занятых должна составить:

62,41 ± 2,8 • 0,408 =62,41 ± 1,14, или от 61,27 до 63,55 млн чел.

В этом случае ввиду слабой колеблемости и малого срока прогноза ошибка прогноза отдельного уровня лишь на 40% боль­ше ошибки положения тренда на 1998 г.

2. Прогноз урожайности зерновых культур во Франции на 2000 г. при многократном выравнивании с учетом тренда ко­леблемости, рассчитанного в разд. 6.4. Прогнозное значение среднего квадратического отклонения урожайности отдельных

лет от ее тренда на 2000 г. составляет: 5(г)^. =5(f)+&s(r) -h = = 3,54+(-0,1235)-17 =1,44. Подставляя его в расчет по формуле для многократного выравнивания, имеем:

Заметим, что из трех слагаемых подкоренного выражения наибольшим является последнее, т.е. S(t)²^, составляющее 57% суммы. Ошибка прогноза уровня урожайности в основном выз­вана колебаниями, возможными в 2000 г., а не ошибкой про­гноза тренда, существенно сниженной применением многократного выравнивания и длинной базой.

S(t)²,,

С вероятностью 0,95 доверительные границы прогноза уро­жайности зерновых культур во Франции, при условии сохране­ния до 2000 г. прежней скорости ее увеличения, составляют:

75,93 ± 2,08 • 1,906 = 75,93 ± 3.96 ц/га.