10.3. Прогноз с учетом случайной колеблемости

При таком прогнозе учитывается как вызванная колебле­мостью ошибка репрезентативности выборочной оценки трен-да, так и колебания уровней в отдельные периоды (моменты) относительно тренда. При этом следует строго различать три вида прогнозов:

• доверительного интервала для линии тренда;

• доверительного интервала для уровня отдельного периода (момента);

• доверительного интервала среднего уровня за ряд перио­дов (моментов).

10.3.1. Прогноз доверительного интервала для линии тренда

Напомним (подробнее см. гл. 7), что средняя ошибка сво­бодного члена линейного тренда составляет:

а, средняя ошибка среднегодового прироста:

(10.1)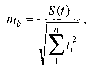

где и - число уровней базы тренда;

S(t) - среднее квадратическое отклонение уровней ряда от трен­да.

Объединяя эти ошибки как независимые по правилу для дис­персий независимых переменных и учитывая, что ошибка сред­негодового прироста за t ^ лет (или иных отрезков времени) возрастет в /^ раз, получаем формулу средней ошибки прогноза для линии тренда на период с удалением t^ от середины базы прогноза:

Вероятность того, что фактическая ошибка не превысит од ного среднего квадратического отклонения, т.е. т,„ равна npi нормальном распределении 0,68. Чтобы получить доверительны! интервал прогноза линии тренда с большей надежностью, напри мер с вероятностью 0,95, среднюю ошибку нужно умножить н< величину г-критерия Стьюдента для вероятности 0,95 и пяти сте пеней свободы вариации (7-2 параметра линейного тренда). По

Итак, с вероятностью 0,95 тренд численности занятых в па-родном хозяйстве РФ в 1998 г. проходит в границах: 62,41±0,81, или от 61,6 до 63,22 млн чел.

При линейном тренде и многократном выравнивании сред­няя ошибка прогноза для линии тренда на период с номером ^ от середины базы примет вид:

(10.3)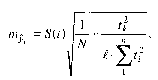

где f. - число сдвигов базы расчета среднегодового прироста Ь;

и- длина каждой базы расчета;

N - общая длина временного ряда.

Например, тренд урожайности зерновых культур во Фран­

ции, рассчитанный в гл. 5, имеет вид:

Средняя ошибка прогноза для линии тренда на 2000 г. с но­мером 17 составит:

Критерий Стыодента при 24 степенях свободы вариации для вероятности 0,95 составит 2,08. Таким образом, с вероятнос­тью 0,95 тренд при сохранении прежней скорости роста уро­жайности в 2000 г. проходит в интервале: 75,93 ± 2,08 • 1,25, или от 72,33 до 78,53 ц/га.

При тренде в форме параболы II порядка параметры а и с не являются не зависимыми друг от друга, и их совокупная ошиб­ка определяется сложнее. Независим от них параметр Ь, ошиб­ка которого аналогична таковой же для линейного тренда. После соединения ошибок всех параметров общая формула средней ошибки прогноза положения параболического тренда на период с номером t^ от середины базы расчета тренда при­обретает вид [18, с. 171]:

(10.4)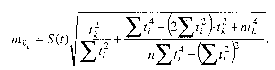

При использовании многократного скользящего выравни-

вания для расчета параметров параболы II порядка знаменате­ли обеих дробей подкоренного выражения умножаются на чис­ло сдвигов базы расчета С, а суммы, стоящие в формулах, исчисляются за одну базу. В числителе же последней дроби бу­дет N-f^.

Для экспоненциального тренда рассчитывается ошибка про­гноза логарифма линии тренда, как для прямой, а затем дове­рительный интервал логари4)ма линии тренда. Его границы потенцируются, получаем несимметрично удаленные от точеч­ного прогноза границы самого прогноза тренда. Для других форм тренда методика расчета средних ошибок и доверитель­ных границ развита недостаточно, многие вопросы остаются спорными и здесь рассматриваться не будут.