Глава 8. Методы изучения и измерения устойчивости уровней ряда и тренда

Устойчивость временного ряда - понятие многоплановое. Его следует рассматривать с двух позиций:

• устойчивости уровней временного ряда;

• устойчивости тенденции (тренда).

Вопрос определения понятия устойчивости невозможно решить без статистической теории динамического ряда, разра­ботанной известными статистиками A.M. Обуховым, Н.С. Чет­вериковым, Альб. Л. Вайнштейном, С.П. Бобровым, Б.С. Ястремским. Согласно этой теории статистический показатель содержит в себе элементы необходимого и случайного. Необ­ходимость проявляется в форме тенденции динамического ряда, случайность - в форме колебаний уровней относитель­но кривой, выражающей тенденцию. Тенденцией характери­зуется процесс эволюции. В явном виде невозможно видеть все причины, порождающие тенденцию (тренд). Полное раз­деление элементов случайного и необходимого существует только в виде научной абстракции.

Расчленение динамического ряда на составляющие элемен­ты - условный описательный прием. Тем не менее, несмотря на взаимозависимость тенденции и колеблемости, решающим фактором, обусловливающим тенденцию, является целенап­равленная деятельность человека, а главной причиной колеб­лемости - изменение условий жизнедеятельности. Исходя из вышеизложенного можно отметить следующее. Устойчивость не означает обязательное повторение одинакового уровня из года в год; такое понимание устойчивости приравнивало бы ее к застойному состоянию изучаемого явления. Слишком уз­ким и жестким было бы понятие устойчивости ряда - как пол­ное отсутствие в динамическом ряду всяких колебаний, так как полностью устранить влияние случайных факторов на по­казатель невозможно. Сокращение колебаний уровней ряда -одна из главных задач при повышении устойчивости, но этим она не исчерпывается, необходимо развитие явления. Отсюда и следует, что устойчивость временного ряда - понятие не про­стое, а многоплановое.

Устойчивость временного ряда - это наличие необходимой тенденции изучаемого статистического показателя с минималь­ным влиянием на него неблагоприятных условий.

Из этого вытекают основные требования устойчивости:

• минимизация колебаний уровней временного ряда;

• наличие определенной, необходимой для общества тен­денции изменения.

Устойчивость временного ряда можно оценивать на различ­ных явлениях. При этом в зависимости от явления будут ме­няться показатели, которые используются в качестве форм выражения существа исследуемого процесса, но содержание понятия устойчивость будет оставаться неизменным.

8.1. Методы измерения устойчивости уровней ряда

Наиболее простым, аналогичным размаху вариации при из­мерении устойчивости уровней временного ряда, является раз­мах колеблемости средних уровней за благоприятные и неблагоприятные, в отношении к изучаемому явлению, перио­ды времени:

(8.1)

Причем к благоприятным периодам времени относятся все периоды с уровнями выше тренда, к неблагоприятным - ниже тренда (однако, например, при изучении динамики производи­тельности труда если это трудоемкость, то все должно быть на­оборот).

Отношение средних уровней за благоприятные периоды вре­мени к средним уровням за неблагоприятные / также может служить показателем устойчивости уровней. Чем ближе отношение к единице, тем меньше колеблемость и соответствен­но выше устойчивость. Назовем это отношение индексом устой­чивости уровней динамических рядов и обозначим:

(8.2)

- отношение средней уровней выше тренда к средней уровней ниже тренда (при тенденции роста).

Например, по данным табл. 5.7 индекс устойчивости уров­ней валового сбора чая в Китае за 1978-1994 гг. составил 1,02.

При измерении колеблемости уровней исчисляются обобща­ющие показатели отклонений уровней от тренда за исследуе­мый период.

Основными абсолютными показателями являются среднее линейное и среднее квадратическое отклонения (см. гл. 6, фор­мулы 6.4; 6.5):

среднее линейное отклонение

(8.3)

среднее квадратическое отклонение

(8.4)

где - фактический уровень;

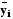- выровненный уровень;

п — число уровней;

р - число параметров тренда;

t - номера лет (знак отклонения от тренда).

Эти показатели выражаются в единицах измерения анали­зируемых уровней и не могут служить для сравнения колеба­ний различных динамических рядов. Сравнение средних линейных и квадратических отклонений по базам скольжения при многократном аналитическом выравнивании дает инфор­мацию о снижении или о повышении устойчивости уровней за период исследования. Аналитическое выравнивание a(t) и Sy(t) и расчет параметров уравнения их трендов позволяют опреде­лить количественные характеристики изменения абсолютной ко­леблемости во времени: среднегодовое изменение, темп изменения. Снижение колеблемости во времени будет равнознач­но повышению устойчивости уровней (см. разд. 6.4).

Для характеристики устойчивости (неустойчивости) Д. Бланфорд и С. Оффат рекомендуют следующие показатели [23]:

1. Процентный размах (Percentage Range) - PR:

(8.5)

PR оценивает разность между максимальным и минималь­ным относительными приростами в процентах.

2. Показатель скользящие средние (Moving Average) - МА, который оценивает величину среднего отклонения от уровня скользящих средних:

(8.6)

3. Среднее процентное изменение (Average Percentage Change) - АРС, которое оценивает среднее значение абсолют­ных величин относительных приростов и квадратов относитель­ных приростов:

(8.7)

Бланфорд и Оффат, анализируя вышеперечисленные коэф­фициенты, отмечают их хорошую согласованность относитель­но коэффициента Спирмена.

Относительные показатели колеблемости, чаще всего ис­пользуемые в статистике, вычисляются делением абсолютных показателей на средний уровень за весь изучаемый период (см. разд. 6.2.2):

коэффициент линейной колеблемости

(8.8) (8.9)

Эти показатели отражают величину колеблемости в сравне­нии со средним уровнем ряда. Они необходимы для сравнения колеблемости двух различных явлений и чаще всего выражают­ся в процентах. Если - коэффициент колеблемости, то величину

(8.10)

называют коэффициентом, устойчивости. Такое определение коэффициента устойчивости интерпретируется как обеспече­ние устойчивости уровней ряда относительно тренда лишь в (100 - 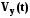) случаях. ЕслиКу составил 0,9, это означает, что среднее колебание составляет 10% среднего уровня. Однако ве­роятность того, что отдельное колебание (т.е. отклонение от тренда в отдельном периоде) не превзойдет средней величины колебаний Sy(t), составляет лишь 0,68, если распределение ко­лебаний по их величине близко к нормальному.

Например (см. гл. 6, разд. 6.2.2), коэффициент колеблемос­ти урожайности зерновых культур во Франции за 1970-1995 гг. составил 6,9%, следовательно, коэффициент устойчивости уров­ней равен 93,1%.