5.4.2. Логарифмическое уравнение тренда

Особенность этого типа тренда заключается в том, что ло­гарифмировать необходимо номера периодов (моментов) вре­мени: = a+b lnt.Следовательно, все номера должны быть по­ложительными числами. Однако это вовсе не означает, что нумерацию следует начинать с числа 1. Дело в том, что величи­на логарифма быстро возрастает при переходе от единицы к двум: натуральный логарифм единицы равен нулю, а логарифм двух равен 0,693, имеем рост на 0,693; в то же время логарифм четырех равен 1,386, а логарифм пяти равен 1,609, имеем при­рост лишь на 0,223 и т.д. Если и уровень изучаемого ряда вна­чале возрастает втрое быстрее, чем между четвертым и пятым периодом, тогда нумерация от единицы допустима. Если же уменьшение прироста уровней происходит значительно медлен­нее, нумерацию периодов (моментов) следует начинать не с еди­ницы, а с большего числа.

Покажем методику расчета логарифмического уравнения тренда на примере динамики валового сбора чая в Китае (см. рис. 4.5; табл. 5.7).

Временной ряд прежде всего нужно разделить на несколько частей, например на три части, и в каждой части вычислить сред­ний уровень, тыс. т:

1978-1983 гг.-331,7;

1984-1989 г. 482,7;

1990-1994 гг. - 566,0.

Эти усредненные уровни относятся соответственно к сере­дине между 1980 и 1981 гг., к середине между 1986 и 1987 гг. и к 1992 г. Если первую дату обозначить годом номер х,то вторая будет годом номерх + 6, а третья - годом номерх + 11,5. Исхо­дя из уравнения логарифмического тренда имеем уравнения:

Таблица 5.7

Расчет логарифмического тренда валового сбора чая в Китае

Год	тыс.т.		ln		-=
1978	268	4	1,386	221	47	2209	235
1979	277	5	1,609	272	5	25	-50
1980	304	6	1,792	314	-10	100	60
1981	343	7	1,946	349	-6	36	-102
1982	397	8	2,079	380	17	289	-102
1983	401	9	2,197	407	-6	36	102
1984	414	10	2,303	431	-17	289	357
1985	432	11	2,398	453	-21	441	252
1986	461	12	2,485	473	-12	144	-216
1987	509	13	2,565	491	18	324	648
1988	545	14	2,639	509	36	1296	396
1989	535	15	2,708	524	11	121	11
1990	540	16	2,773	539	1	1	-11
1991	542	17	2,833	553	-11	121	66
1992	560	18	2,890	566	-6	36	-132
1993	600	19	2,944	578	22	484	-44
1994	588	20	2,996	590	-2	4	-
Итого	7716	-	-	7650	k=6	652,6	1470

Делим второй результат на первый:

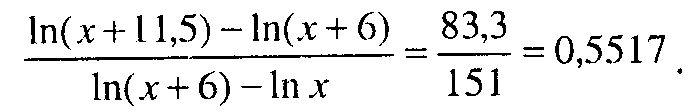
Это число говорит о степени замедления роста средних уров­ней между подпериодами ряда. Теперь необходимо подобрать такое значение х,при котором получаем наибольшее прибли­жение к рассчитанному показателю замедления роста уровней.

При х= 2 получим:, что слишком мало.

Увеличим хдо 6:

,- все еще ниже наблюдаемой величины. Примемх =8:- что уже больше наблюдаемого значения.

При х = 7 имеем:

- немного больше необходимого.

Можно, принимая дробные значения х, подойти еще ближе к фактическому значению, однако вряд ли целесообразно при­менять мелкодробные номера периодов времени, да и сам про­цесс усреднения уровней по подпериодам ряда включает субъективные моменты, поэтому лучше ограничиться прибли­жениемх6,5 лет, следовательно, середина между 1980 и 1981 гг. - это номер 6,5 от начала отсчета номеров лет, тогда 1978г. - это номерt= 4. Исходя из этого нумеруем все года в табл. 5.7, начиная сt= 4 доt= 20.

Зная величину x= 6,5, подставляем ее в уравнения (5.21) и (5.22), чтобы вычислить по ним величину параметраb.Из (5.21):

откуда b= 230,9.

Из уравнения (5.22):

откуда b =228,4.

Принимаем среднее из двух независимых оценок параметра b,равное 229,6.

Теперь, подставляя значения хиbв уравнения (5.18), (5.19) и (5.20), получим три независимые оценки параметра а:

Средняя оценка параметра аравна (-97,6). Итак, уравнение логарифмического тренда имеет вид:

где t=0 в 1974г.

По этому уравнению рассчитаны уровни тренда в табл. 5.7. Хотя суммы уровней немного разошлись, кривая, как видно на рис. 4.5, хорошо отражает тенденцию.