
К тесту по ВЫШКЕ / АД / 8__mypage.i-exam.ru_index
.pdf
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
Преподаватель: Тимошин М.И.
Специальность: 140604.65 - Электропривод и автоматика промышленных установок и технологических комплексов
Группа: Ад-31 Дисциплина: Математика
Идентификатор студента: ГИЛЬФАНОВ Р.Р.
Логин: 07ps122659
Начало тестирования: 2013-04-04 13:38:00 Завершение тестирования: 2013-04-04 14:58:20 Продолжительность тестирования: 80 мин. Заданий в тесте: 44 Кол-во правильно выполненных заданий: 22
Процент правильно выполненных заданий: 50 %
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 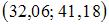 для оценки математического ожидания
для оценки математического ожидания
нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
36,62
36,52
9,12
73,24
Решение:
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Статистическое распределение выборки
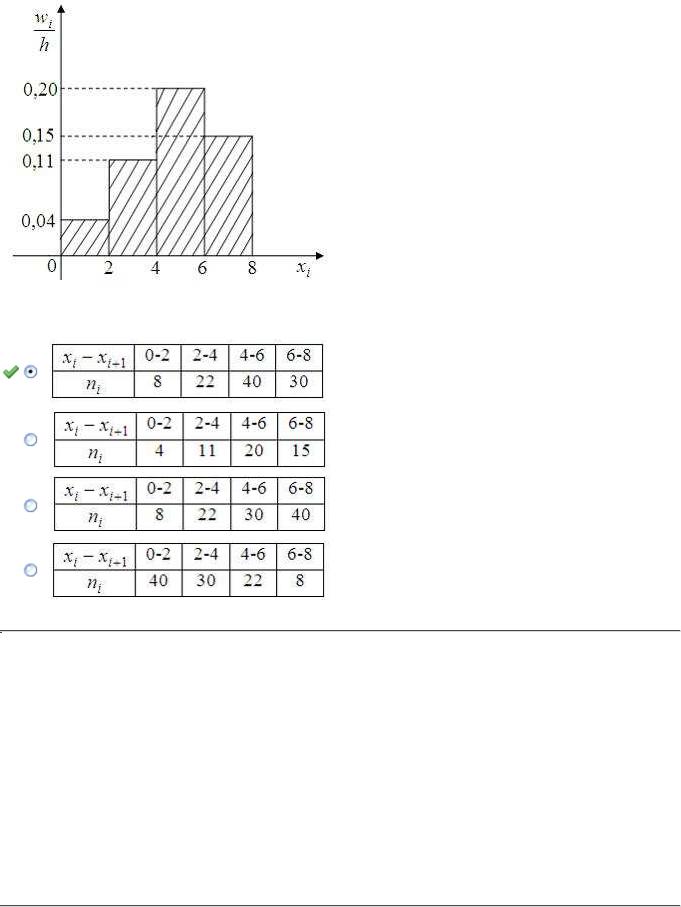
Из генеральной совокупности извлечена выборка объема  , гистограмма относительных частот которой имеет вид
, гистограмма относительных частот которой имеет вид
Стр. 1 из 20 |
12.04.2013 13:40 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
Тогда статистическое распределение выборки можно определить как …
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
Если все варианты 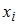 исходного вариационного ряда увеличить в четыре раза, то выборочное среднее
исходного вариационного ряда увеличить в четыре раза, то выборочное среднее 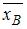 …
…

 увеличится в четыре раза
увеличится в четыре раза
 увеличится в два раза
увеличится в два раза
 не изменится
не изменится  увеличится на четыре единицы
увеличится на четыре единицы
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
При построении выборочного уравнения прямой линии регрессии Y на X вычислены выборочный коэффициент регрессии  и выборочные средние
и выборочные средние  и
и
Стр. 2 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
 Тогда уравнение регрессии примет вид …
Тогда уравнение регрессии примет вид …
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Прямая на плоскости |
|
|
Прямая отсекает на оси Oy отрезок |
и имеет угловой коэффициент |
Тогда ее |
уравнение имеет вид … |
|
|
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Поверхности второго порядка
Центр сферы  имеет координаты …
имеет координаты …
Решение:
Уравнение сферы радиуса R с центром в точке  имеет вид:
имеет вид:
Выделим в исходном уравнении полные квадраты:
или
Тогда центр сферы имеет координаты 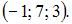
Стр. 3 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  имеет вид …
имеет вид …
Решение:
Уравнение плоскости, параллельной плоскости 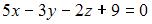 имеет вид:
имеет вид:
 Подставим координаты точки
Подставим координаты точки  в это уравнение:
в это уравнение:
 Тогда
Тогда 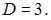
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Прямоугольные координаты на плоскости
Точки 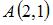 и
и  лежат на одной прямой, параллельной оси ординат. Расстояние между точками A и M равно 6. Тогда положительные координаты точки M равны …
лежат на одной прямой, параллельной оси ординат. Расстояние между точками A и M равно 6. Тогда положительные координаты точки M равны …
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Даны два вектора:  и
и  Тогда вектор
Тогда вектор  , перпендикулярный и вектору
, перпендикулярный и вектору  и вектору
и вектору  можно представить в виде …
можно представить в виде …
Стр. 4 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Градиент скалярного поля
Направление наибыстрейшего возрастания функции  задается вектором …
задается вектором …
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Норма вектора в евклидовом пространстве
Скалярное произведение векторов 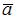 и
и 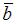 равно 8, угол между векторами равен
равно 8, угол между векторами равен
норма вектора  равна 4. Тогда норма вектора
равна 4. Тогда норма вектора  равна …
равна …
4
2
3
Решение:
Так как |
то |
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Численные методы решения дифференциальных уравнений и систем
На рисунке изображена интегральная кривая, являющаяся решением задачи Коши
Стр. 5 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
Выполнен один шаг метода Эйлера с шагом  Тогда точка
Тогда точка  …
…

 лежит ниже интегральной кривой
лежит ниже интегральной кривой
 лежит выше интегральной кривой
лежит выше интегральной кривой
 лежит на интегральной кривой
лежит на интегральной кривой  может лежать как ниже, так и выше интегральной кривой
может лежать как ниже, так и выше интегральной кривой
Решение:
По рисунку видим, что в некоторой окрестности точки x0, в которую попадает и x1, интегральная кривая выпукла вниз и находится над касательной, построенной в точке  Поэтому точка
Поэтому точка 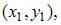 находящаяся на этой касательной, будет
находящаяся на этой касательной, будет
лежать ниже интегральной кривой.
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Функция представлена таблицей:
Тогда в интерполяционном полиноме Лагранжа 2-ой степени с узлами 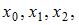 составленном по этой таблице для приближенного вычисления
составленном по этой таблице для приближенного вычисления  при условии
при условии  значение
значение  не может быть равно …
не может быть равно …
8
23
12
20
Решение:
Для получения интерполяционного полинома Лагранжа 2-ой степени требуются три
Стр. 6 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
узла 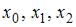 и значения данной функции в них:
и значения данной функции в них:  Это могут быть любые три точки
Это могут быть любые три точки  из таблицы, удовлетворяющие двум условиям:
из таблицы, удовлетворяющие двум условиям:
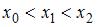 и
и  Следовательно, в качестве узла
Следовательно, в качестве узла  нельзя брать 0, 1, 3, 4. Следовательно,
нельзя брать 0, 1, 3, 4. Следовательно,  не может принимать значения 2, 3, 5 или 8.
не может принимать значения 2, 3, 5 или 8.
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Численное дифференцирование и интегрирование
Метод трапеций дает приближенное значение интеграла |
… |

 с избытком
с избытком
 с недостатком
с недостатком
 точно
точно  про которое ничего определенного сказать нельзя
про которое ничего определенного сказать нельзя
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
0,0081
0,081
0,06
0,0729
Решение:
Воспользуемся формулой Бернулли:
, где  ,
,  ,
,  ,
, 
Тогда
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
Стр. 7 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина X задана плотностью распределения вероятностей
Тогда математическое ожидание a и среднее квадратическое
отклонение  этой случайной величины равны …
этой случайной величины равны …
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
Решение:
Для вычисления события A (среди отобранных деталей нет годных) воспользуемся
Стр. 8 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
формулой |
где n – общее число возможных элементарных исходов |
испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть 
А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три бракованные детали из пяти, то есть  Следовательно,
Следовательно,
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Числовые последовательности
Общий член числовой последовательности |
имеет вид … |
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Область сходимости степенного ряда
Область сходимости степенного ряда |
имеет вид … |
[– 2; 2) (– 2; 2) (– 2 2] [– 2; 2]
 ЗАДАНИЕ N 21 отправить сообщение разработчикам
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Сходимость числовых рядов
Стр. 9 из 20 |
12.04.2013 13:40 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122659
Сумма числового ряда |
равна … |
 ЗАДАНИЕ N 22 отправить сообщение разработчикам
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Однородные дифференциальные уравнения
Дифференциальное уравнение 
будет однородным дифференциальным уравнением первого порядка при  равном …
равном …
24
0
18
3
Решение: |
|
|
Запишем уравнение в виде |
Это уравнение будет однородным, |
|
если функция |
|
будет однородной относительно и |
нулевого порядка, то есть при |
|
|
Тогда |
и |
|
 ЗАДАНИЕ N 23 отправить сообщение разработчикам
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

 уравнением с разделяющимися переменными
уравнением с разделяющимися переменными  линейным дифференциальным уравнением 1-го порядка
линейным дифференциальным уравнением 1-го порядка
Стр. 10 из 20 |
12.04.2013 13:40 |
