К тесту по ВЫШКЕ / АД / 6__mypage.i-exam.ru_index
.pdf
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
Преподаватель: Тимошин М.И.
Специальность: 140604.65 - Электропривод и автоматика промышленных установок и технологических комплексов
Группа: Ад-31 Дисциплина: Математика
Идентификатор студента: ЩЕГОЛЕВ Н.В.
Логин: 07ps122681
Начало тестирования: 2013-04-04 13:37:50 Завершение тестирования: 2013-04-04 14:57:58 Продолжительность тестирования: 80 мин. Заданий в тесте: 44 Кол-во правильно выполненных заданий: 19
Процент правильно выполненных заданий: 43 %
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Прямая на плоскости
В треугольнике с вершинами 
уравнение высоты,
проведенной из вершины C, имеет вид …
Решение:
Воспользуемся уравнением прямой, проходящей через точку 
перпендикулярно нормальному вектору |
В |
|
качестве нормального вектора возьмем вектор |
а в качестве заданной |
|
точки возьмем точку |
Тогда |
или |
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Поверхности второго порядка
Уравнение поверхности второго порядка
определяет …
эллипсоид
параболоид
конус 
однополостный гиперболоид
Стр. 1 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
Решение:
Выделим в уравнении 
полные квадраты:
или
Разделив обе части последнего уравнения на 6, получим уравнение которое определяет эллипсоид.
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Прямоугольные координаты на плоскости
Даны три вершины параллелограмма: 
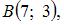
Тогда четвертая вершина 
противолежащая вершине B, имеет координаты …
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Угол между плоскостями 
и 
равен …
0
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …
Стр. 2 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
Решение:
Интервальная оценка математического ожидания нормально распределенного количественного признака симметрична относительно его точечной оценки. Таким свойством обладает интервал 
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии Y на X имеет вид 
Тогда выборочный коэффициент корреляции может быть равен …
0,82
–0,82
1,2
–1,2
Решение:
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку 
а во-вторых, его знак совпадает со знаком выборочного
коэффициента регрессии. Этим условиям удовлетворяет значение 
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 
полигон частот которой имеет вид:
Стр. 3 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
Тогда статистическое распределение выборки можно определить как …
Решение:
Вычислим предварительно частоту варианты 
как 
Так как относительные частоты 
вычисляются по
формулам |
, где |
– частота варианты , а |
– объем выборки, то |
статистическое распределение данной выборки может иметь вид:
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …
Стр. 4 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
0,13
0,065
3,9
0,7
Решение:
Несмещенная оценка дисперсии вычисляется по формуле:
где |
Вычислив предварительно |
получаем
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Периодические функции
Период функции 
равен …
Решение: |
|
|
|
|
Период функции cos 5x равен |
период функции |
равен |
||
Наименьшее число T, при делении которого на |
и |
|
||
на получаются целые числа, есть число |
которое и будет периодом исходной |
|||
функции. |
|
|
|
|
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Гармонические колебания
Стр. 5 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
Угловая частота гармонических колебаний равна |
начальная фаза |
рад, а |
смещение колеблющейся точки от нулевого положения через 2 секунды равно 0,1. Тогда амплитуда гармонических колебаний составляет …
0,2
0,1
0,02
Решение:
Уравнение гармонических колебаний имеет вид: |
Следовательно, |
или
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Элементы гармонического анализа
Функцией, ортогональной к функции 
на
не является …
Решение: |
|
|
|
|
Функции |
и |
называются ортогональными на |
|
|
если |
|
|
|
|
Любые две функции системы: |
|
|
||
ортогональны в промежутке длины |
поэтому функция |
на |
||
|
не ортогональна функции |
так как |
|
|
Стр. 6 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент a0 в разложении 
-периодической функции
равен …
0,5
Решение:
Так как функция 
не является ни четной, ни нечетной, то вычислим ее
коэффициент Фурье по формуле:
Тогда
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции |
равно … |
1
4
3
2
Решение:
Точку 
называют точкой разрыва функции 
если она не является
непрерывной в этой точке. В частности, точками разрыва данной функции могут являться точки, в которых знаменатель равен нулю, то есть 
Однако область определения функции 
определяется как 
то есть имеет вид 
Тогда 
имеет одну точку разрыва:
Стр. 7 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
удовлетворяющую условию
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции |
имеет вид … |
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
равна …
Решение:
Стр. 8 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
Площадь данной фигуры можно вычислить по формуле |
где |
||
|
a – « левая», b – « правая» точки пересечения |
|
|
параболы |
и прямой |
Определим значения a и b, решив |
|
уравнение |
Получаем |
Тогда |
|
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка |
функции |
имеет вид … |
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Числовые последовательности
Общий член числовой последовательности |
имеет вид … |
Стр. 9 из 22 |
12.04.2013 13:38 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122681
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Сходимость числовых рядов
Сходящимся является числовой ряд …
Решение:
Из представленных числовых рядов сходящимся является ряд
Действительно, так как при применении теоремы сравнения со сходящимся
обобщенным гармоническим рядом получаем:
А это означает, что ряд |
сходится. |
|
Для рядов |
и |
не выполняется необходимое условие |
сходимости, а расходимость ряда |
устанавливается сравнением с |
|
гармоническим рядом. |
|
|
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Область сходимости степенного ряда
Стр. 10 из 22 |
12.04.2013 13:38 |