К тесту по ВЫШКЕ / АД / 12__mypage.i-exam.ru_index
.pdf
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
Преподаватель: Тимошин М.И.
Специальность: 140604.65 - Электропривод и автоматика промышленных установок и технологических комплексов
Группа: Ад-31 Дисциплина: Математика
Идентификатор студента: ЕКИМОВА О.С.
Логин: 07ps122661
Начало тестирования: 2013-04-04 13:40:09 Завершение тестирования: 2013-04-04 15:00:13 Продолжительность тестирования: 80 мин. Заданий в тесте: 44 Кол-во правильно выполненных заданий: 28
Процент правильно выполненных заданий: 63 %
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка |
функции |
имеет вид … |
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции |
равно … |
4
2
1
3
Решение:
Стр. 1 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
Точку 
называют точкой разрыва функции 
если она не является непрерывной в этой точке. В частности, точками разрыва данной функции являются точки, в которых знаменатели равны нулю. То есть 
и
Тогда
Следовательно, получили четыре точки разрыва функции.
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
равна …
Решение:
Площадь данной фигуры можно вычислить по формуле |
где |
a – « левая», b – « правая» точки пересечения параболы 
и прямой 
Определим значения a и b, решив
Стр. 2 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
уравнение |
Получаем |
Тогда |
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции |
имеет вид … |
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Умножение матриц
Матрица |
где |
и |
Тогда элемент |
равен …
10
4
– 3 0
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Стр. 3 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
Система |
совместна, если не равно … |
2
– 2
– 1 1
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель |
равен … |
0
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
За базис трехмерного векторного пространства можно принять совокупность векторов …
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …
0,57
Стр. 4 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
0,43
0,55
0,53
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Для дискретной случайной величины X:
функция распределения вероятностей имеет вид:
Тогда значение параметра p может быть равно … |
|
|
|
0,655 |
|
|
|
1 |
|
|
|
0,25 |
|
|
|
0,45 |
|
|
|
Решение: |
|
|
|
По определению |
Следовательно, |
и |
Этим |
условиям удовлетворяет, например, значение 
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Определение вероятности
Внутрь круга радиуса 5 наудачу брошена точка. Тогда вероятность того, что точка окажется внутри вписанного в круг равностороннего треугольника, равна …
Стр. 5 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Числовые характеристики случайных величин
Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание M(X) и дисперсия D(X) дискретной случайной величины X – числа появлений события A в 
проведенных испытаниях равны …
, 
, 
, 
, 
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 
, гистограмма относительных частот которой имеет вид
Тогда значение a равно …
0,11
0,12
0,09
0,14
Стр. 6 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
Решение:
Так как площадь гистограммы относительных частот равна 1, то 
Тогда 
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал (16,64; 18,92) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …
(17,18; 18,38)
(16,15; 19,41)
(17,18; 18,92)
(16,15; 18,38)
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 
где точечная оценка математического
ожидания 
а точность оценки 
В случае увеличения объема выборки точность оценки улучшается, то есть значение 
будет меньше 1,14.
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
Если все варианты 
исходного вариационного ряда увеличить в четыре раза, то выборочное среднее 
…
увеличится в четыре раза
увеличится в два раза
не изменится 
увеличится на четыре единицы
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии Y на X имеет вид 
Тогда выборочный коэффициент корреляции может быть равен …
0,82
Стр. 7 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
–0,82
1,2
–1,2
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Площадь параллелограмма, построенного на векторах 
и 
равна …
3
6
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Норма вектора в евклидовом пространстве
Если 
и 
– ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что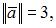 
то норма вектора 
равна …
5
25
1
– 1
Решение: |
|
|
Так как |
то |
и |
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Градиент скалярного поля
Модуль градиента скалярного поля 
в точке 
равен 5 при 
равном …
Стр. 8 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
2
4
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Плоскости 
и 
перпендикулярны при значении m,
равном …
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Поверхности второго порядка |
|
|
Плоскость |
касается поверхности |
в точке с |
координатами … |
|
|
Решение:
Координаты точки касания найдем из решения системы |
. |
Подставляя в первое уравнение |
получим |
или, |
выделив полный квадрат, 
Тогда 
То есть точка касания имеет координаты 
Стр. 9 из 20 |
12.04.2013 13:43 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122661
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Прямая на плоскости
В треугольнике с вершинами 
уравнение высоты,
проведенной из вершины C, имеет вид …
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Прямоугольные координаты на плоскости
В треугольнике с вершинами 
и 
проведена биссектриса AM.
Тогда координаты точки M равны …
ЗАДАНИЕ N 24 отправить сообщение разработчикам
Тема: Метрические пространства
Расстояние между точками |
и |
в метрике |
, где 
и 
, равно …
4
2
0
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Отображение множеств
Отображение |
действует по правилу: |
Тогда f ([0, 2]) |
Стр. 10 из 20 |
12.04.2013 13:43 |