
К тесту по ВЫШКЕ / АД / __mypage.i-exam.ru_index.php_menu
.pdf
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655
уравнений |
или |
Решая эту систему, находим значения постоянных величин  Поэтому решение задачи Коши имеет вид:
Поэтому решение задачи Коши имеет вид: 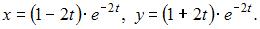
 ЗАДАНИЕ N 35 отправить сообщение разработчикам
ЗАДАНИЕ N 35 отправить сообщение разработчикам
Тема: Однородные дифференциальные уравнения
Интегральные кривые уравнения  имеют вид …
имеют вид …
Решение:
Данное уравнение является однородным дифференциальным уравнением первого
порядка. Сделаем замену |
тогда |
и |
Уравнение запишется |
|
в виде: |
|
Сократив на и разделив переменные, |
||
получим: |
Проинтегрируем обе части: |
или |
||
где |
|
. Сделаем обратную замену: |
|
|
 ЗАДАНИЕ N 36 отправить сообщение разработчикам
ЗАДАНИЕ N 36 отправить сообщение разработчикам
Тема: Типы дифференциальных уравнений
Уравнение 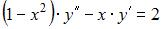 является …
является …
дифференциальным уравнением второго порядка, допускающим понижение порядка линейным неоднородным дифференциальным уравнением второго порядка с
постоянными коэффициентами линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами  уравнением Эйлера
уравнением Эйлера
Стр. 21 из 26 |
11.04.2013 18:33 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655
 ЗАДАНИЕ N 37 отправить сообщение разработчикам
ЗАДАНИЕ N 37 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Вектор  является линейной комбинацией векторов
является линейной комбинацией векторов  и
и 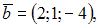 если
если  то
то  равно …
равно …
3
2
– 2
– 3
Решение:
 ЗАДАНИЕ N 38 отправить сообщение разработчикам
ЗАДАНИЕ N 38 отправить сообщение разработчикам
Тема: Умножение матриц
Даны матрицы |
и |
Тогда матрица |
имеет вид … |
Решение:
Произведением 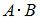 матрицы A размера
матрицы A размера 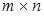 на матрицу B размера
на матрицу B размера 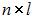 называется матрица C размера
называется матрица C размера  , элемент которой
, элемент которой  равен сумме
равен сумме
произведений соответственных элементов i-й строки матрицы A и j-го столбца матрицы B. Тогда
Стр. 22 из 26 |
11.04.2013 18:33 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655
 ЗАДАНИЕ N 39 отправить сообщение разработчикам
ЗАДАНИЕ N 39 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Методом Крамера не может быть решена система линейных уравнений …
Решение:
Систему линейных алгебраических уравнений можно решить методом Крамера, если ее определитель не равен нулю.
1. Из системы |
получим |
|
следовательно, система может быть |
решена методом Крамера. |
|
2. Из системы |
, получим |
следовательно, система может быть решена методом Крамера. |
|
3. Из системы |
получим |
|
следовательно, система может быть |
решена методом Крамера. |
|
4. Из системы |
получим |
следовательно, система не может быть решена методом Крамера.
 ЗАДАНИЕ N 40 отправить сообщение разработчикам
ЗАДАНИЕ N 40 отправить сообщение разработчикам
Тема: Вычисление определителей
Стр. 23 из 26 |
11.04.2013 18:33 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655
Корень уравнения |
равен … |
– 1
– 5 1 5
Решение:
Определитель второго порядка вычисляется по формуле:
. Тогда
По условию задачи определитель должен равняться  то есть
то есть 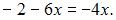 Следовательно,
Следовательно, 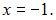
 ЗАДАНИЕ N 41 отправить сообщение разработчикам
ЗАДАНИЕ N 41 отправить сообщение разработчикам
Тема: Метрические пространства
Функция
заданная на множестве целых чисел …

 удовлетворяет всем трем аксиомам метрического пространства
удовлетворяет всем трем аксиомам метрического пространства
 не удовлетворяет аксиоме тождества
не удовлетворяет аксиоме тождества
 не удовлетворяет аксиоме симметрии
не удовлетворяет аксиоме симметрии  не удовлетворяет аксиоме треугольника
не удовлетворяет аксиоме треугольника
 ЗАДАНИЕ N 42 отправить сообщение разработчикам
ЗАДАНИЕ N 42 отправить сообщение разработчикам
Тема: Элементы теории множеств
Даны три множества:
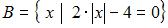 и
и 
Тогда число элементов множества  равно …
равно …
4 |
Решение:
Сначала определим множества 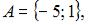
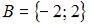 и
и 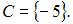
Так как множество D строится как объединение трех множеств, то результатом будет такое множество чисел, которому принадлежит и множество A и множество B
Стр. 24 из 26 |
11.04.2013 18:33 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655
и множество C. Тогда множество  содержит четыре элемента.
содержит четыре элемента.
 ЗАДАНИЕ N 43 отправить сообщение разработчикам
ЗАДАНИЕ N 43 отправить сообщение разработчикам
Тема: Отображение множеств
Прообразом множества 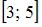 при отображении
при отображении  является …
является …
Решение:
Прообразом множества 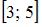 при отображении
при отображении 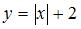 являются те точки
являются те точки  которые при данном отображении попадают в
которые при данном отображении попадают в  В нашем случае это множество
В нашем случае это множество
 ЗАДАНИЕ N 44 отправить сообщение разработчикам
ЗАДАНИЕ N 44 отправить сообщение разработчикам
Тема: Мера плоского множества
Мера плоского множества, изображенного на рисунке,
равна …
0
Решение:
Мера плоского множества равна площади соответствующей фигуры, то есть для ее
Стр. 25 из 26 |
11.04.2013 18:33 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655
определения из площади квадрата со стороной 4 нужно вычесть площадь четвертой части круга радиуса 4. Следовательно, мера этого множества равна 
Стр. 26 из 26 |
11.04.2013 18:33 |
