К тесту по ВЫШКЕ / АД / __mypage.i-exam.ru_index.php_menu

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

Преподаватель: Тимошин М.И.

Специальность: 140604.65 - Электропривод и автоматика промышленных установок и технологических комплексов

Группа: Ад-31 Дисциплина: Математика

Идентификатор студента: АКСАМЕНТОВА Л.А.

Логин: 07ps122655

Начало тестирования: 2013-04-04 13:38:13 Завершение тестирования: 2013-04-04 14:13:36 Продолжительность тестирования: 35 мин. Заданий в тесте: 44 Кол-во правильно выполненных заданий: 14

Процент правильно выполненных заданий: 31 %

ЗАДАНИЕ N 1 отправить сообщение разработчикам

Тема: Точечные оценки параметров распределения

Если все варианты 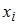исходного вариационного ряда уменьшить в два раза, то выборочное среднее квадратическое отклонение …

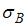уменьшится в два раза

увеличится в два раза

не изменится уменьшится в четыре раза

Решение:

Для исходного вариационного ряда выборочное среднее квадратическое отклонение можем вычислить по формуле где выборочная дисперсия вычисляется

как

Тогда для нового вариационного ряда

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

ЗАДАНИЕ N 2 отправить сообщение разработчикам

Тема: Интервальные оценки параметров распределения

Построен доверительный интервал для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при уменьшении объема выборки в два раза значение точности этой оценки …

увеличится в раз

уменьшится в два раза

увеличится в два раза уменьшится в 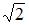раз

Решение:

Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде

значение аргумента функции Лапласа 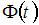, при котором , –

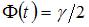надежность оценки.

Тогда в случае уменьшения объема выборки в два раза значение точности оценки увеличится в 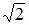раз.

ЗАДАНИЕ N 3 отправить сообщение разработчикам

Тема: Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема n = 100:

Тогда относительная частота варианты равна …

0,25

0,75

0,24

0,04

ЗАДАНИЕ N 4 отправить сообщение разработчикам

Тема: Элементы корреляционного анализа

При построении выборочного уравнения прямой линии регрессии Y на X вычислены

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

выборочный коэффициент регрессии и выборочные средние и Тогда уравнение регрессии примет вид …

Решение:

Выборочное уравнение прямой линии регрессии Y на X имеет вид

Тогда или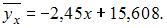

ЗАДАНИЕ N 5 отправить сообщение разработчикам

Тема: Числовые последовательности

значение a5 равно …

Решение:

Подставим в формулу общего члена значение n=5. Тогда

ЗАДАНИЕ N 6 отправить сообщение разработчикам

Тема: Сходимость числовых рядов

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

5

1

Решение:

Представим общий член этого ряда в виде суммы

геометрические прогрессии. Следовательно, эти ряды сходятся, причем:

Таким образом, сумма данного числового ряда равна:

ЗАДАНИЕ N 7 отправить сообщение разработчикам

Тема: Область сходимости степенного ряда

[– 2; 2) (– 2; 2) (– 2 2] [– 2; 2]

Решение:

Вычислим предварительно радиус сходимости этого ряда по формуле

то есть:

1)вычислим предел

2)для любого натурального 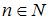справедливо

Следовательно, ряд сходится.

Таким образом, область сходимости примет вид

ЗАДАНИЕ N 8 отправить сообщение разработчикам

Тема: Основные методы интегрирования

Решение:

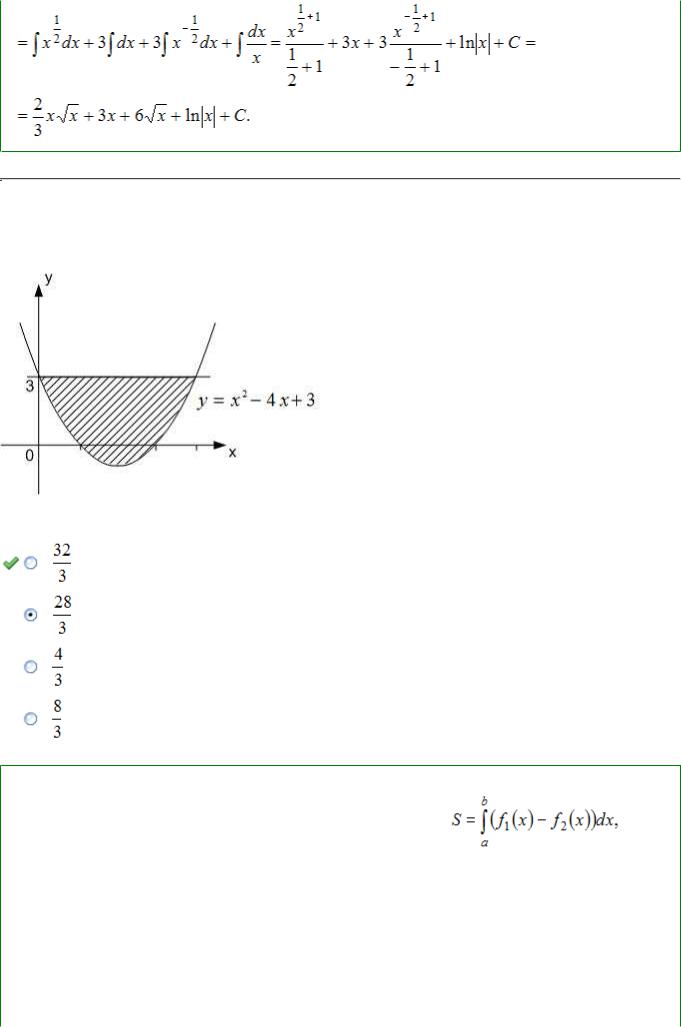
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

ЗАДАНИЕ N 9 отправить сообщение разработчикам

Тема: Приложения определенного интеграла

Площадь фигуры, изображенной на рисунке

равна …

Решение:

b – « правая» точка пересечения параболы

и прямой Определим значение b, решив уравнение Получаем: Тогда

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

ЗАДАНИЕ N 10 отправить сообщение разработчикам

Тема: Непрерывность функции, точки разрыва

1

2

0

Решение:

Данная функция определена и непрерывна на каждом из интервалов и меняет свое аналитическое выражение в точках и

Поэтому функция может иметь разрыв только в этих точках. Исследуем их на

непрерывность.

Для точки вычислим односторонние пределы и значение функции в этой точке:

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

и

первого рода.

ЗАДАНИЕ N 11 отправить сообщение разработчикам

Тема: Дифференциальное исчисление ФНП

2

– 2 1

ЗАДАНИЕ N 12 отправить сообщение разработчикам

Тема: Численное дифференцирование и интегрирование

Значение дифференцируемой функции y = f (x) в точке 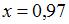можно приближенно найти как …

ЗАДАНИЕ N 13 отправить сообщение разработчикам

Тема: Численные методы решения дифференциальных уравнений и систем

На рисунке изображена интегральная кривая, являющаяся решением задачи Коши

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

Выполнен один шаг метода Эйлера с шагом Тогда точка …

лежит ниже интегральной кривой

лежит выше интегральной кривой

лежит на интегральной кривой может лежать как ниже, так и выше интегральной кривой

Решение:

По рисунку видим, что в некоторой окрестности точки x0, в которую попадает и x1, интегральная кривая выпукла вниз и находится над касательной, построенной в точке Поэтому точка находящаяся на этой касательной, будет

лежать ниже интегральной кривой.

ЗАДАНИЕ N 14 отправить сообщение разработчикам

Тема: Интерполирование функций: интерполяционные полиномы Лагранжа

Функция представлена таблицей:

Тогда график многочлена, интерполирующего эту функцию, пересекает ось в точке с абсциссой …

5,5

11

6

0

Решение:

Через две точки проходит единственный полином 1-ой степени, графиком которого является прямая. Для получения интерполяционного полинома Лагранжа 1-ой степени требуются два узла и значения данной функции в них :

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122655

Подставим в эту формулу

Чтобы получить абсциссу точки пересечения этой прямой с осью абсцисс, приравняем 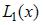к нулю: то есть

ЗАДАНИЕ N 15 отправить сообщение разработчикам

Тема: Системы линейных уравнений с комплексными коэффициентами

Если и являются решением системы линейных уравнений

, то равно …

2

32

0

Решение:

Решим систему методом Крамера. Для этого вычислим определитель системы:

и вспомогательные определители:

и

Тогда

по формулам Крамера получим:

и

Следовательно,

ЗАДАНИЕ N 16 отправить сообщение разработчикам

Тема: Комплексные числа и их представление

Изображение комплексного числа z на комплексной плоскости представлено на рисунке.