
К тесту по ВЫШКЕ / АД / 7__mypage.i-exam.ru_index
.pdf
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
Преподаватель: Тимошин М.И.
Специальность: 140604.65 - Электропривод и автоматика промышленных установок и технологических комплексов
Группа: Ад-31 Дисциплина: Математика
Идентификатор студента: УСТЮГОВ А.К.
Логин: 07ps122673
Начало тестирования: 2013-04-04 13:48:03 Завершение тестирования: 2013-04-04 15:00:37 Продолжительность тестирования: 72 мин. Заданий в тесте: 44 Кол-во правильно выполненных заданий: 21
Процент правильно выполненных заданий: 47 %
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид …
имеет вид …
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле 
Тогда
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
Не является непрерывной на отрезке  функция …
функция …
Стр. 1 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
равна …
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Частная производная |
функции |
имеет вид … |
Стр. 2 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Мера плоского множества
Мера плоского множества  равна …
равна …
4
1
2
0
Решение:
Мера плоского множества  равна площади
равна площади
соответствующей фигуры, то есть квадрата со стороной 2. Следовательно, мера этого множества равна 4.
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Отображение множеств
Из представленных отображений  не является инъективным …
не является инъективным …
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Метрические пространства
Расстояние между функциями 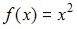 и
и  пространства всех непрерывных действительных функций, определенных на отрезке
пространства всех непрерывных действительных функций, определенных на отрезке  с метрикой
с метрикой
равно …
Стр. 3 из 23 |
12.04.2013 13:39 |
http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
2
1
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Элементы теории множеств
Даны множества: 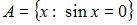 и
и  Тогда число элементов,
Тогда число элементов,
принадлежащих их пересечению равно …
3
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …
Решение:
Для вычисления события A (среди отобранных деталей нет бракованных)
воспользуемся формулой |
где n – общее число возможных элементарных |
исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть  А общее число благоприятствующих исходов равно числу способов,
А общее число благоприятствующих исходов равно числу способов,
которыми можно извлечь три небракованные детали из семи, то есть 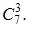
Стр. 4 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
Следовательно,
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:
И вероятность  Тогда значения a, b и c могут быть равны …
Тогда значения a, b и c могут быть равны …
a = 0,05, b = 0,30, с = 0,25
a = 0,05, b = 0,30 с = 0,35
a = 0,05, b = 0,20 с = 0,35
a = 0,15, b = 0,30 с = 0,25
Решение:
Так как сумма вероятностей возможных значений X равна 1, то  А так как
А так как  то
то
 Следовательно,
Следовательно,  , и, например,
, и, например, 

 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Числовые характеристики случайных величин
Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание M(X) и дисперсия D(X) дискретной случайной величины X – числа появлений события A в 
проведенных испытаниях равны …
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
Банк выдает 35% всех кредитов юридическим лицам, а 65% – физическим лицам.
Стр. 5 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,1. Тогда вероятность непогашения в срок очередного кредита равна …
0,1175
0,125
0,8825
0,1275
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Дано трехмерное векторное пространства с базисом  Если векторы
Если векторы  и
и  то вектор
то вектор  может иметь вид …
может иметь вид …
Решение:
Три вектора образуют базис, если определитель, составленный из координат этих векторов, не равен нулю. Так как и то
Тогда  Этому условию удовлетворяет, например, вектор
Этому условию удовлетворяет, например, вектор  то есть Остальные векторы, представленные среди ответов, не удовлетворяют
то есть Остальные векторы, представленные среди ответов, не удовлетворяют
данному условию.
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Вычисление определителей
Корень уравнения |
равен … |
– 4 i
Стр. 6 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
– 4
4
16i
Решение:
Определитель третьего порядка можно вычислить, например, разложением по элементам первой строки:
По условию задачи определитель должен равняться 4x, то есть  Следовательно,
Следовательно, 
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Умножение матриц |
|
|
|
Даны матрицы |
и |
Если матрица |
вырожденная, то |
значение a равно …
– 6
5
– 5
0
Решение:
Произведением  матрицы A размера
матрицы A размера  на матрицу B размера
на матрицу B размера  называется матрица C размера
называется матрица C размера  , элемент которой
, элемент которой  равен сумме
равен сумме
произведений соответственных элементов i-ой строки матрицы A и j-го столбца матрицы B. Тогда
Матрица называется вырожденной, если ее определитель равен нулю. Тогда
Стр. 7 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Система |
совместна, если не равно … |
2
– 2
– 1 1
Решение:
Система линейных уравнений совместна, если ранг основной матрицы системы равен рангу расширенной матрицы.
Расширенная матрица системы имеет вид Вычислим, например, минор
третьего порядка этой матрицы не содержащий элемент :
 Ранг расширенной матрицы равен трем. Тогда ранг
Ранг расширенной матрицы равен трем. Тогда ранг
матрицы системы должен быть равен трем (определитель матрицы системы не равен нулю). Из этого условия находим :
Значит 
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Комплексные числа и их представление
Комплексное число задано в показательной форме  Тогда его алгебраическая форма записи имеет вид …
Тогда его алгебраическая форма записи имеет вид …
Стр. 8 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
Решение:
Показательная форма комплексного числа имеет вид:
аалгебраическая –  Так как
Так как
аглавное значение аргумента  определяется из системы уравнений
определяется из системы уравнений
то для нахождения параметров  и
и  получим систему:
получим систему:
В нашем случае:
Следовательно, 
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Дифференцирование функции комплексного переменного |
|
|
Значение производной функции |
в точке |
равно … |
Решение: |
|
Производная функции |
имеет вид |
Стр. 9 из 23 |
12.04.2013 13:39 |

http://mypage.i-exam.ru/index.php?menu=show_test&login=07ps122673
Тогда
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Системы линейных уравнений с комплексными коэффициентами
Решение системы уравнений |
имеет вид … |
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Градиент скалярного поля
Направление наибыстрейшего возрастания функции  задается вектором …
задается вектором …
 ЗАДАНИЕ N 21 отправить сообщение разработчикам
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Площадь параллелограмма, построенного на векторах  и
и  равна …
равна …
3
6
Стр. 10 из 23 |
12.04.2013 13:39 |
