РЕШЕНИЯ / Теория с Формулами

В данном цикле процессы 2 → 3 и 4 → 1 адиабатические, следовательно, совершаются без теплообмена с окружающей средой. Тепло от нагревателя газ получает только в процессе 1 → 2.

Процесс 1 → 2 изобарический, поэтому

Q1 = νСр(T2 − T1 ).

Газ отдает тепло в изобарическом процессе 4 → 1, поэтому

Q2 = νСр(T3 − T4 ).

Рассмотрим подробнее полученное выражение. Процессы 1 → 2 и 3 → 4 изобарические, для них справедливы равенства:

Для адиабатических процессов 2 → 3 и 4 → 1 справедливы соотношения

Сравнивая равенства (1) и (4), видим, что Т3 = T2 , следовательно, выра-

Т4 T1

жение для КПД принимает вид

51

η = 1 − Т4 .

Т1

Преобразуем это выражение. Запишем соотношение между давлением и температурой в состояниях 1 и 4, используя уравнение адиабаты р1−γТγ = const

Тогда выражение для КПД цикла можно записать с использованием одной из его характеристик – степени повышения давления

З а д а ч а 16

Найти изменение ∆S энтропии при переходе m = 8 г кислорода от объема

Изменение энтропии (функции состояния системы) не зависит от способа перехода системы из состояния 1 в состояние 2.

По первому началу термодинамики для идеального газа

δQ = δA +dU = pdV + 2i νRdT.

52

Подставим данные задачи и произведем вычисления:

Ответ: изменение энтропии при переходе кислорода из состояния 1 в состоя-

ние 2 ∆S = 5,4 Дж/К.

53

Домашнее задание

Номер варианта указывается преподавателем, номера задач приведены в табл. 6.

Таблица 6

1. Взяв исходной общую для всех графиков точку, изобразить для идеального газа примерные графики изохорического, изобарического, изотермического и адиабатического процессов на диаграммах:

а) р–V, U–V;

б) V–T, U–T; в) p–T, U–p; г) V–T, U–p; д) р–Т, U–V.

2.При изобарическом сжатии азота была совершена работа, равная 12 кДж. Определить количество полученного газом тепла и изменение его внутренней энергии.

3.Азот нагревался при постоянном давлении, причем ему было сообщено количество теплоты 21 кДж. Определить работу, которую совершил газ, и изменение его внутренней энергии.

4.Водород массой 10 г нагрели на 200 К, причем газу было передано количество теплоты 40 кДж. Найти изменение внутренней энергии водорода и совершенную им работу.

5.В закрытом сосуде объемом 10 л находится воздух под давлением 105 Па. Какое количество тепла надо сообщить воздуху, чтобы повысить давление в сосуде в 5 раз?

6.В баллоне объемом 1,0 10–3 м3 находится кислород при температуре 300 К. Газу было сообщено 8,4 кДж теплоты. Определить температуру и давление газа после нагревания.

54

7.Один моль кислорода, находившегося при температуре 320 К, адиабатически сжали так, что его давление возросло в 10 раз. Найти: 1) температуру газа после сжатия; 2) работу, совершаемую над газом.

8.Некоторое количество идеального газа с трехатомными жесткими молекулами перешло адиабатически из состояния с температурой 280 К в состояние с

температурой 320 К, с давлением 2 105 Па и объемом 50 л. Определить первоначальный объем газа и совершенную газом работу.

9.Идеальный газ с показателем адиабаты 1,4, находившийся при температуре 160 К, адиабатически сжали так, что объем уменьшился в 10 раз. Определить:

1)температуру газа после сжатия; 2) работу, совершаемую над газом.

10.321 г гелия (температура 293 К, давление 105 Па) сжимают адиабатически до давления 107 Па. Определить: 1) температуру газа в конце сжатия; 2) работу, совершаемую газом.

11.Сероводород H2S массой 6 кг, занимающий объем 3 м3 при температуре 270С, сжали адиабатически так, что давление его увеличилось в 2 раза. Определить конечный объем и изменение внутренней энергии газа.

12.Изобразить график процессов, описанных в подпунктах а – е, на диа-

грамме р–V и определить: приращение внутренней энергии газа; работу, совершаемую газом; количество полученного или отданного газом тепла:

а) ν молей идеального двухатомного газа, имевшего первоначально давление

р1 и объем V1, адиабатически сжимают до объема V2, а затем изотермически расширяют до прежнего объема;

б) ν молей идеального одноатомного газа, имевшего первоначально давление р1 и температуру Т1, изотермически сжимают до давления р2, а затем адиабатически расширяют до прежнего объема;

в) ν молей идеального двухатомного газа, имевшего первоначально давление

р1 и объем V1, адиабатически расширяют до давления р2, а затем изотермически сжимают до первоначального давления;

г) ν молей идеального газа с показателем адиабаты γ, имевшего первоначально температуру Т1 и объем V1, адиабатически расширяют до температуры Т2, а затем изотермически сжимают до прежнего объема;

д) ν молей идеального газа с показателем адиабаты γ, имевшего первона-

чально давление р1 и температуру Т1, изотермически расширяют до давления р2, а затем адиабатически сжимают до первоначального давления;

е) ν молей идеального газа с показателем адиабаты γ, имевшего первоначально температуру Т1 и объем V1, изотермически расширяют до объема V2, а затем адиабатически сжимают до прежнего объема.

13. Найти молярные теплоемкости сV и ср смесей:

а) одноатомного и двухатомного газов (количество вещества одноатомного газа 0,4 моля, а двухатомного – 0,2 моля);

б) кислорода массой 6 г и азота массой 3 г;

55

в) одноатомного и трехатомного газов (количество вещества одноатомного газа 2 моля, а трехатомного – 3 моля);

г) гелия массой 5 г и водорода массой 2 г; д) азота массой 7 г и аргона массой 20 г.

14. Для описанных в подпунктах а – д политропических процессов, происходящих в компрессорах, определить: показатель политропы; молярную теплоемкость газа; работу, совершенную газом; приращение внутренней энергии газа; количество полученного газом тепла. Показать примерный ход процесса на диа-

грамме р–V и сравнить его с адиабатой и изотермой, проведенными из одного и того же начального состояния до одинакового конечного объема:

а) идеальный газ с показателем адиабаты 1,4 сжимается от объема 10 л до объема 5 л. Давление при этом возрастает от 1 105 до 5 105 Па;

б) один моль идеального одноатомного газа расширяется по закону р = аV, где а = 0,5 107 Па/м3, от объема 0,02 м3 до объема 0,05 м3;

в) два моля идеального одноатомного газа расширяется по закону V = ар, где а = 5 10–7 м3/Па. Давление при этом возрастает от 1 105 до 3 105 Па;

г) 1 кг воздуха нагревают от температуры 3 102 К до температуры 6,4 102 К. Первоначальное давление 1 105 Па, конечное – 7,3 105 Па;

д) один моль идеального двухатомного газа сжимается по закону V = a/T, где а = 0,3 м3/К. Температура при этом возрастает от 225 до 400 К.

21.Двухатомный газ совершает цикл Карно. Определить КПД цикла, если

известно, что на каждый киломоль этого газа при его адиабатическом сжатии затрачивается работа 2 МДж. Температура нагревателя 1270 С.

22.Двухатомный газ совершает цикл Карно, причем при изотермическом расширении его объем увеличивается в 2 раза, а при последующем адиабатическом расширении он производит работу 300 Дж. Определить работу, совершаемую газом за один цикл.

23.Двухатомный газ совершает цикл Карно, причем при изотермическом расширении его объем увеличивается в 2 раза. Работа, совершаемая газом за цикл,

А= 7,2 кДж. Определить работу адиабатического сжатия.

24.Двухатомный газ совершает цикл Карно, причем объем газа при адиабатическом расширении меняется от 12 до 16 л. Определите КПД цикла.

25.Двухатомный газ совершает цикл Карно, КПД которого 20%. Определите, во сколько раз увеличивается объем газа при адиабатическом расширении.

26.Один киломоль двухатомного газа совершает цикл Карно, КПД которого 30%. Температура нагревателя 400 К. Какова работа адиабатического сжатия газа?

27.Один киломоль кислорода О2 совершает цикл Карно в интервале температур от 27 до 3270 С. Наивысшее давление при этом 20 105 Па. Вычислить КПД цикла и количество тепла, полученного от нагревателя.

56

28.1 кг воздуха совершает цикл Карно в интервале температур от 27 до 6270С. При этом минимальный объем газа 43 л, а максимальный 86 л. Определите термический КПД цикла и количество подведенного тепла.

29.1 кг воздуха совершает цикл Карно в интервале температур от 30 до 2500С. Наивысшее давление 20.105 Па, наименьшее 1,2.105 Па. Определите термический КПД цикла и работу, совершенную газом за цикл.

30.1 кг воздуха совершает цикл Карно в интервале температур от 27 до 6270С, причем наивысшее давление 60.105 Па, а совершенная за цикл работа 42,1 кДж. Определить термический КПД цикла и максимальный и минимальный объемы газа.

31.Для описанных ниже циклов, совершаемых одним молем двухатомного идеального газа определите: 1) параметры характерных точек циклов; 2) количество подведенного и отведенного тепла; 3) работу, совершенную газом за цикл;

4)термический КПД цикла. Сравните полученное значение КПД с КПД цикла Карно, изотермы которого соответствуют наибольшей и наименьшей температурам рассматриваемого цикла:

а) цикл поршневого двигателя внутреннего сгорания с подводом тепла при постоянном объеме состоит из двух адиабатических и двух изохорических (рис.

28 а) процессов. Известно, что V1/V2 = 6; р1 = 105 Па; T1 = 300 К и р3/р2 = 1,6; б) цикл поршневого двигателя внутреннего сгорания с подводом тепла при

постоянном давлении состоит из двух адиабатических, одного изобарического и одного изохорического (рис. 28 б) процессов. Известно, что р1 = 105 Па; T1 =

= 300 K; V1/V2 = 12,5; V3 = 2V2;

в) цикл газотурбинной установки с подводом тепла при постоянном давлении состоит из двух адиабатических и двух изобарических (рис. 28 в) процессов. Из-

вестно, что р1 = 105 Па; T1 = 290 K; T3 = 600 K; р2 = 8р1;

г) цикл состоит из двух изотермических и двух изохорических (рис. 28 г)

процессов. Известно, что р1 = 1,5.105 Па; T1 = 290 K; р3 = 10р1; T1 = 290 K; р3 =

= 10р1; T3 = 480 K;

д) рабочий цикл идеальной паровой машины (рис. 28 д). Известно, что V0 =

= 0,5 л; V1 = 1,5 л; V2 = 3 л; р0 = 1 атм; р1 = 12 атм. Процесс 3–4 адиабатический с показателем адиабаты 1,33 (газ в этом случае считать многоатомным);

е) цикл Ленуара состоит из изохорического, адиабатического и изобарического (рис. 28 е) процессов. Известно, что р1 = 0,1 МПа; р2 = 0,2 МПа; T1 = 300 K.

32. Для цикла поршневого двигателя внутреннего сгорания с подводом тепла при постоянном объеме (цикл Отто), состоящего из двух адиабат и двух изохор

(рис. 28 а), известна степень адиабатического сжатия ε = V1/V2. Найти КПД цик-

ла, если показатель степени адиабаты равен γ.

33. Цикл поршневого двигателя внутреннего сгорания с подводом тепла при постоянном давлении (цикл Дизеля) состоит из двух адиабат, одной изобары и

одной изохоры (рис. 28 б). Отношение ε=V1/V2 называется степенью адиабатиче-

57

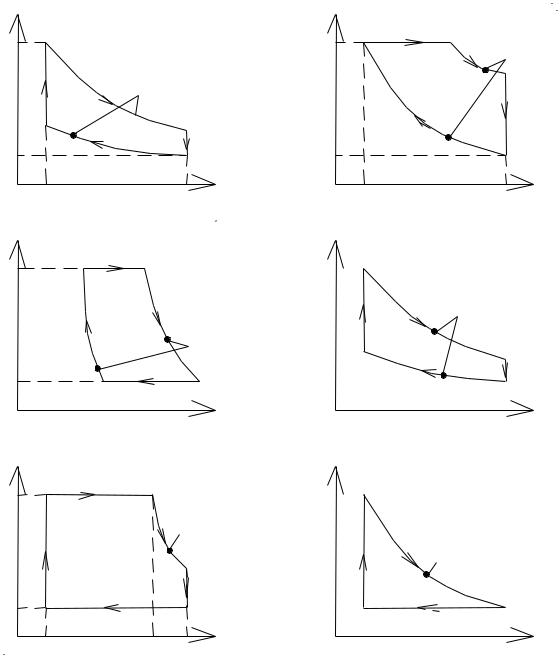
ского сжатия, отношение ρ = V3/V2 – степенью предварительного расширения. Найти КПД цикла, если показатель степени адиабаты равен γ.

34. Для цикла Ленуара (рис. 28 а), состоящего из изохоры, адиабаты и изобары, найдите КПД цикла, если известна степень повышения давления р2/р1 и показатель адиабаты γ.

58

Контрольная работа

Ва р и а н т 1

1.28 г азота, находящегося при температуре 400С и давлении 750 мм рт.ст., сжимают адиабатически до объема 13 л. Найти температуру и давление азота после сжатия, работу сжатия.

2.1 моль идеального двухатомного газа совершает цикл, состоящий из двух

изохор и двух изобар. Наименьший объем Vмин = 10 л, наименьшее давление

рмин = 246 кПа, наибольшее рмах = 410 кПа. Начертить график цикла. Определить: 1) температуру газа для характерных точек цикла, 2) теплоту Q1, получен-

ную газом от нагревателя, 3) теплоту Q2, переданную газом охладителю, 4) термический КПД цикла.

Ва р и а н т 2

1.Одноатомный газ, занимающий объем 20 л под давлением 10 атм, был изобарически нагрет от 50 до 2000 С. Найти работу расширения газа, количество тепла, переданное газу.

2.14 г азота N2 адиабатически расширяются так, что давление уменьшается в 5 раз, затем изотермически сжимаются до первоначального давления и изобари-

чески переводятся в первоначальное состояние. Начальная температура азота 4200С, начальное давление 1 МПа. Определить: 1) параметры характерных точек цикла; 2) работу, совершенную газом за цикл; 3) термический КПД цикла.

Ва р и а н т 3

1.При адиабатическом сжатии 2 г азота, имеющего температуру 270 С, объем газа уменьшился в 10 раз. Определить конечную температуру газа и работу сжатия.

2.Один моль идеального двухатомного газа, находящийся под давлением

р1 = 0,1 МПа при температуре Т1 = 300 К, нагревают при постоянном объеме до давления 0,2 МПа. После этого газ изотермически расширился до начального давления р1, а затем изобарически был сжат до начального объема V1. Начертите график цикла. Определите: 1) температуру газа для характерных точек цикла; 2) теплоту Q1, полученную газом от нагревателя; 3) теплоту Q2, переданную газом охладителю; 4) работу, совершаемую газом за весь цикл; 5) термический КПД цикла.

59

Ва р и а н т 4

1.В закрытом сосуде находится 16 г кислорода при давлении 1 атм и температуре 270 С. После нагревания давление в сосуде повысилось до 5 атм. Найти: до какой температуры нагрелся газ, каков объем сосуда, какое количество теплоты сообщено газу?

2.Одноатомный газ в количестве ν = 0,1 кмоль, имевший при давлении

р1 = 100 кПа объем V1 = 5 м3, сжимался изобарически до объема V2 = 1 м3, затем сжимался адиабатически и, наконец, расширялся при постоянной температуре до начального объема и давления. Найти: 1) температуру, объем и давление, соответ-

ствующие характерным точкам цикла, 2) теплоту Q1, полученную газом от нагревателя, 3) теплоту Q2, переданную газом охладителю, 4) работу, совершенную газом за весь цикл, 5) термический КПД цикла.

Ва р и а н т 5

1.Один киломоль азота, находящегося при нормальных условиях, адиабатически расширяется, увеличивая объем в 5 раз. Найти: работу, совершенную при расширении, изменение внутренней энергии газа.

2.Окись углерода массой 5 кг расширяется при постоянном давлении, совершая работу в 105 Дж, а затем охлаждается до прежней температуры при постоянном объеме, после чего сжимается изотермически до первоначального объема.

Изобразите цикл на диаграмме р–V и определите: 1) температуру в конце изобарического расширения; 2) количество теплоты, полученной системой при изобарическом процессе; 3) термический КПД цикла. Начальная температура газа

T1 = 373 K.

60