АРХИТЕКТУРЫ
ВЫЧИСЛИТЕЛЬНЫХ
СИСТЕМ
ЦИФРОВОЙ ЛОГИЧЕСКИЙ УРОВЕНЬ:
ВЕНТИЛИ И БУЛЕВА АЛГЕБРА
ВЕНТИЛИ
Цифровая схема – это схема, в которой есть только два логических значения
Обычно сигнал от 0 до 1В представляет одно значение (например, 0), а сигнал от 2 до 5В – другое значение (например, 1)
Крошечные электронные устройства, которые называются вентилями, могут вычислять различные функции от этих двузначных сигналов
Вся современная цифровая логика
основывается на том, что транзистор может
работать как очень быстрый переключатель |
2 |
|
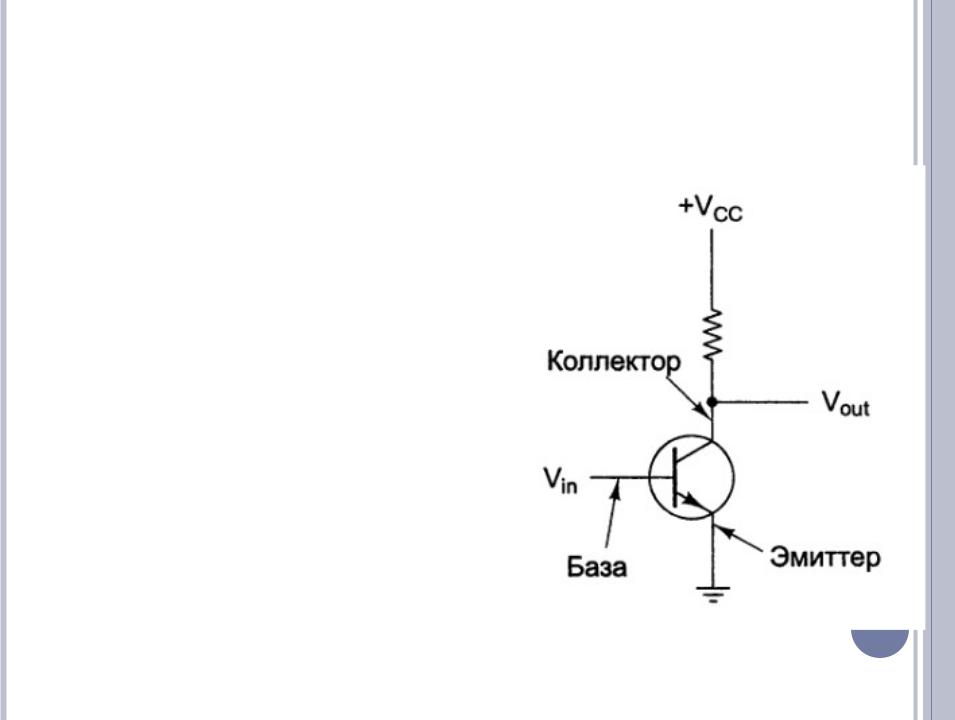
ТРАНЗИСТОРНЫЙ ИНВЕРТОР
Транзистор |
|
имеет |
три |
соединения: коллектор, базу и |
|||
эмиттер. |
Если |
входное |
|
напряжение Vin ниже порогового, |
|||
то транзистор |
действует как |
||
очень большое |
сопротивление. |
||
Следствие – Vout=+Vcc.
Если входное напряжение Vin выше порогового, то транзистор действует как проводник. Следствие – Vout=0В.
Вывод: логический 0 переходит в логическую 1, логическая 1
переходит в логический 0. |
3 |
|
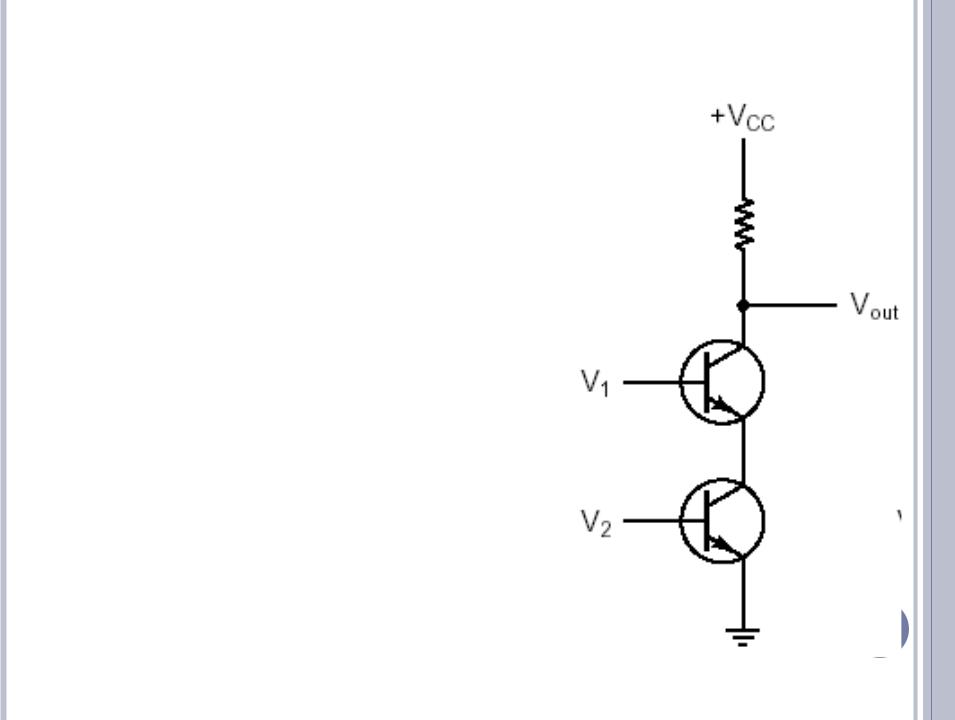
ВЕНТИЛЬ НЕИ
Два транзистора соединены последовательно. Если на входе V1 и V2 высокие, то Vout = 0В.
Если одно из входных
напряжений низкое, Vout высокое.
Вывод: логические 1 и 1 переходят в логический 0, все остальные комбинации переходят в логическую 1.
4
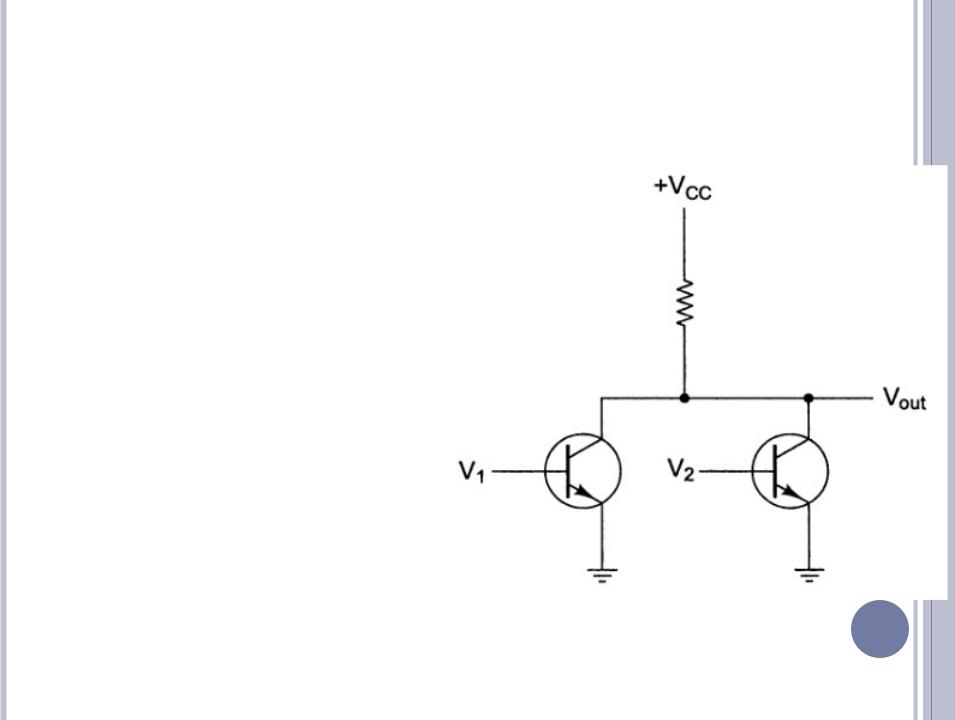
ВЕНТИЛЬ НЕИЛИ
Два транзистора соединены параллельно. Если на входе один из сигналов высокий,
то Vout=0В.
Если оба входных сигнала низкие, Vout высокое.
Вывод: логические 0 и 0 переходят в логическую 1, все остальные комбинации переходят в логический 0.
5
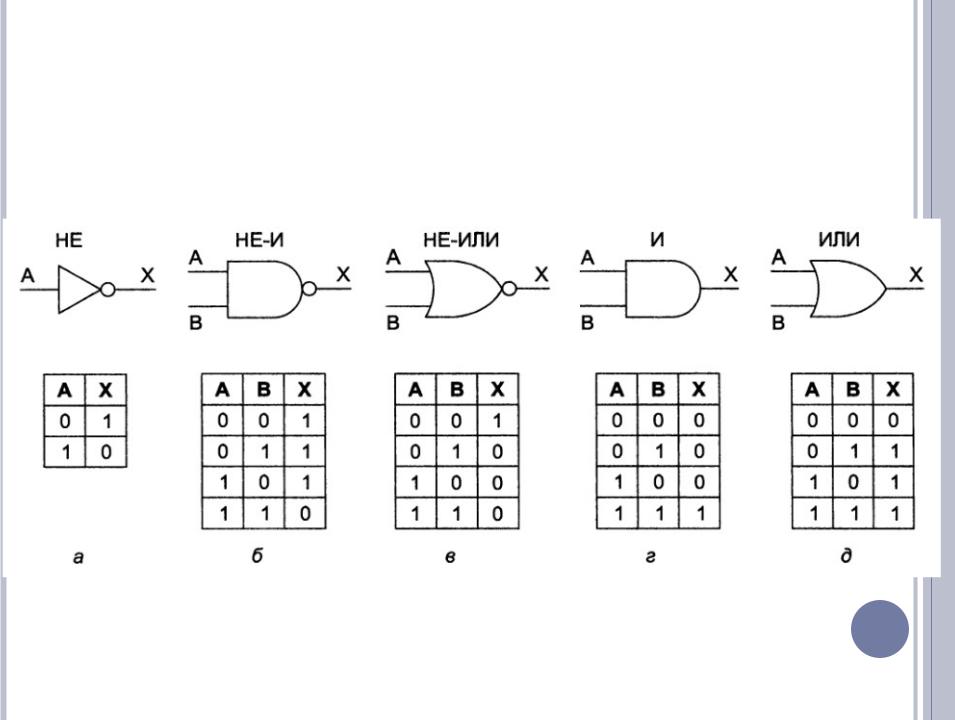
ИЗОБРАЖЕНИЯ 5 ОСНОВНЫХ ВЕНТИЛЕЙ
6
БУЛЕВА АЛГЕБРА
Требуется использование особой алгебры, в которой все переменные и функции могут принимать только два значения: 0 или 1.
Булева алгебра названа в честь английского математика Джорджа Буля (18151864).
Булева функция имеет только 2^n возможных комбинаций в зависимости от n переменных.
Все значения вполне можно уместить в таблице, которую принято называть таблицей истинности.
Если договориться аргумент записывать по возрастанию, то функцию можно записать
строкой. Например, НЕИ – 1110, НЕИЛИ – 1000, |
|
И – 0001 и т.д. |
7 |
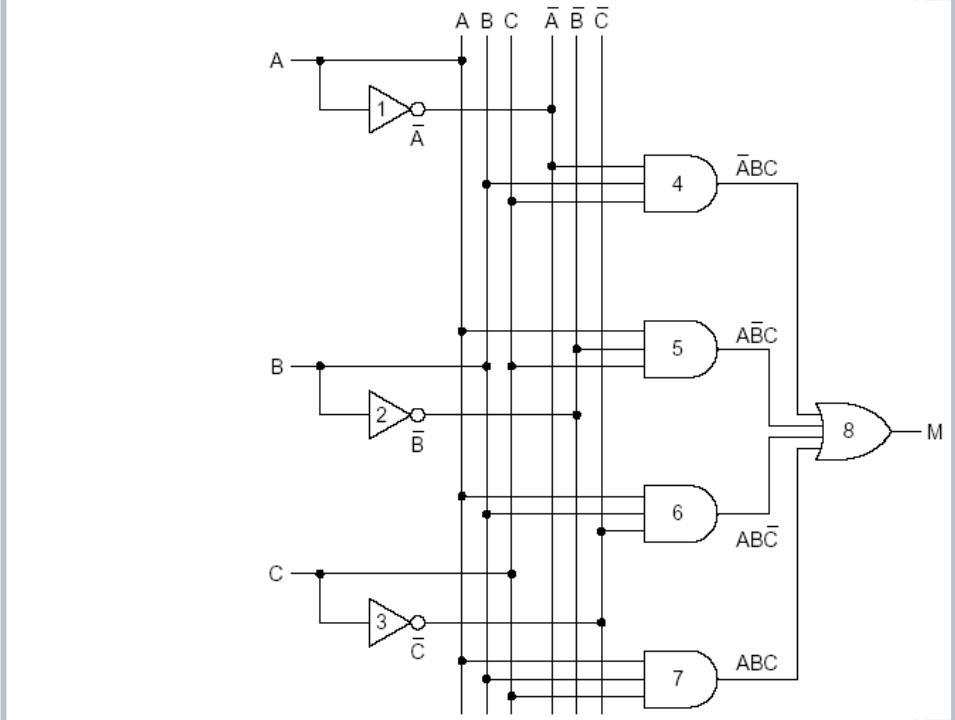
ФУНКЦИЯ
БОЛЬШИНС ТВА ОТ ТРЕХ ПЕРЕМЕНН
ЫХ
M=F(A,B,C |
8 |
|
|
) |
|
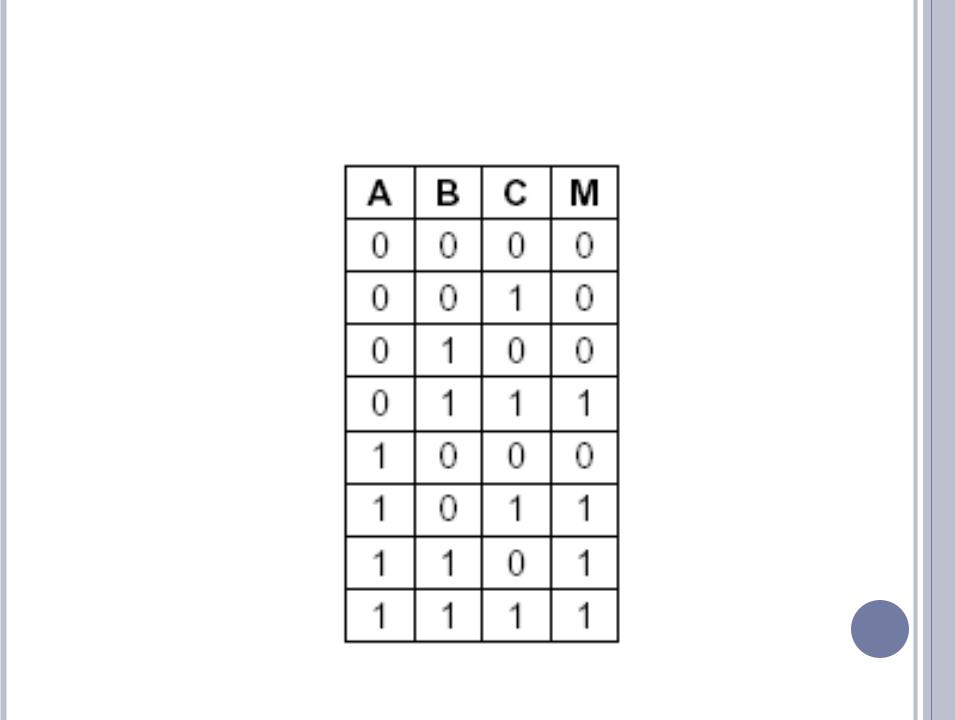
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ФУНКЦИИ БОЛЬШИНСТВА
9
АЛЬТЕРНАТИВНЫЙ ВИД ЗАПИСИ
Любую булеву функцию можно определить, указав, какие комбинации значений дают значение функции 1.
Для обозначения инвертирования переменной будем рисовать над ней черту. Кроме этого, для обозначения булевой функции И будем использовать знак умножения, для ИЛИ – знак сложения.
Например,
_
АВС принимает значение 1, только если А=1, В=0, С=1
__
АВ+ВС принимает значение 1, только если (А=1 и В=0) или
(В=1 и С=0)
Для функции большинства от трех переменных:
_ _ _
М=АВС+АВС+АВС+АВС
10