мат.анализ / 3.4. Формы контроля (текущего, промежуточного, рубежного, итогового) Э МА

3.4. Формы текущего, промежуточного, рубежного и итогового контроля

Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов проводится в следующих формах: итоговый контроль (экзамены 1, 2 семестры) оцениваются по системе: неудовлетворительно, удовлетворительно, хорошо, отлично; зачет (1 семестр) оценивается по системе: зачет, незачет; на практических занятиях контроль осуществляется при ответе у доски, при проверке домашних заданий, выполнении контрольных и индивидуальных работ.

Оценочные средства для текущего контроля успеваемости студентов заочной формы обучения, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов проводится в следующих формах: итоговый контроль (экзамен 2 семестр) оцениваются по системе: неудовлетворительно, удовлетворительно, хорошо, отлично; зачет (1 семестр) оценивается по системе: зачет, незачет; контрольные работы проводятся в аудитории и оцениваются по системе неудовлетворительно, удовлетворительно, хорошо, отлично.

Для получения результирующей оценки итогового контроля используются следующие баллы:

• за контрольные работы – максимально-20 баллов;

• за домашние работы – максимально-10 баллов;

• за текущую работу на семинарских занятиях – максимально-10 баллов;

• за зачет – максимально-20 баллов;

• за экзамен – максимально-40 баллов.

Итоговый контроль (экзамены) оцениваются по системе:

- неудовлетворительно - в сумме набрано 0-30 баллов;

- удовлетворительно - в сумме набрано 31-49 баллов;

- хорошо - в сумме набрано 50-75 баллов;

- отлично - в сумме набрано 76-100 баллов

Примерные вопросы к экзамену (1 семестр)

1. Теорема о гранях.

2. Теоремы о пределе последовательности.

3. Теорема об ограниченной последовательности.

4. Теорема о трех пределах.

5. Теорема о сходимости монотонной последовательности.

6. Число е.

7. Теорема о разности монотонно возрастающей и монотонно убывающей последовательностях.

8. Лемма о вложенных отрезках.

9. Условие Коши сходимости последовательности (док. необходимость).

10. Свойства сходящихся рядов.

11. Необходимый признак сходимости рядов.( liman=0)

12. Признаки сравнения рядов.

13. Признак Даламбера.

14. Признак Коши.

15. Признак Лейбница.

16. 1-й и 2-й замечательные пределы.

17. Свойства пределов.

18. Классификация бесконечно малых.

19. Шкала, эквивалентность, главная часть бесконечно малых.

20. Непрерывность функции. Разрывы.

21. Первая теорема Больцано-Коши.

22. Вторая теорема Больцано-Коши.

23. Формула для приращения функции.

24. Производная сложной функции.

25. Правила вычисления производных.

26. Производная обратной функции.

27. Дифференциал. Связь между дифференцируемостью и существованием производной.

28. Правила дифференцирования. Дифференциал n-го порядка.

29. Инвариантность формы первого дифференциала.

30. Лемма о возрастании и убывании функции.

31. Теорема Ферма.

32. Теорема Ролля.

33. Теорема Лагранжа.

34. Теорема Коши.

35. Формула Тейлора.

36. Правило Лопиталя.

37. Исследование функций (экстремум, выпуклость, точки перегиба, асимптоты).

38. Функция нескольких переменных. Предел, непрерывность.

39. Производные, полное приращение, полный дифференциал функции нескольких переменных.

40. Производная сложной функции нескольких переменных.

41. Инвариантность формы первого дифференциала функции нескольких переменных.

42. Второй дифференциал функции нескольких переменных.

43. Формула Тейлора функции нескольких переменных.

44. Производные неявных функций.

45. Экстремум функции нескольких переменных. Необходимые условия экстремума.

46. Достаточные условия экстремума функции нескольких переменных.

47. Условный экстремум. Метод множителей Лагранжа.

48. Теорема о первообразной.

49. Свойства неопределенных интегралов. Правила интегрирования.

50. Рекуррентная формула для неопределенных интегралов .

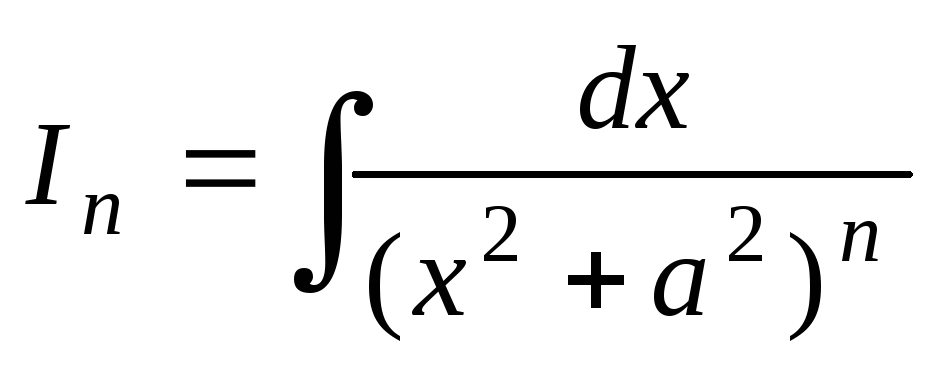51. Интегрирование правильных дробей.

52. Подстановки Эйлера.

53. Определенный интеграл. Свойства сумм Дарбу.

54. Свойства определенных интегралов.

55. Теорема о среднем значении.

56. Непрерывность функции .

57. Основная формула интегрального исчисления.

58. Несобственный интеграл первого рода. Теоремы о сходимости.

59. Несобственный интеграл второго рода. Теоремы о сходимости.

60. Комплексные числа. Тригонометрическая и показательная формы комплексного числа.

61. Обыкновенные дифференциальные уравнения. Задача Коши. Уравнение Бернулли.

62. Дифференциальные уравнения второго порядка с постоянными коэффициентами (однородные и неоднородные)

Примерное зачетное задание 1 семестр

№п/п	Задание	Ответ
1	Установите соответствие между пределами и их значениями: 1. 2. 3.	А) 0 Б) В) 2
2	Расположите функции по возрастанию их точек разрыва	А) Б) В) Г)
3	Значение производной функции в точке равно…
4	Точка перегиба графика функции имеет координаты…	а) (-3;56) б) (-3;-56) в) (3; 110) г) (0; 2)
5	Частную производную имеют три следующие функции	а) б) в) г)
6	Последовательность задана формулой общего члена , расположите члены последовательности в порядке возрастания их порядкового номера	А) 1,5 Б) В) -4 Г) -
7	Множество всех первообразных имеет вид…	а) в) б) г)
8	Площадь фигуры изображенной на рисунке определяется интегралом	А) Б) В) Г)
9	Несобственным интегралом является интеграл…	а) б) в)
10	Повторный интеграл сводится к определенному интегралу	А) Б) В)
11	Разделение переменных в дифференциальном уравнении приведет его к виду…	А) б) В) г)
12	Общее решение линейного дифференциального уравнения полученного методом Бернулли имеет вид…	А) Б) В) Г)
13	Общее решение дифференциального уравнения имеет вид	А) Б) В) Г)
14	Установить соответствие между дифференциальным уравнением и названием: 1. 2. 3.	А) линейное дифференциальное уравнение Б) однородное дифференциальное уравнение В) уравнение с разделяющимися переменными
15	Четвертый член числового ряда равен…	А) Б) В) Г) -
16	Используя признак Даламбера исследовать на сходимость ряды: А) В)	1) ряд А сходится, В расходится 2) ряды А и В расходятся 3) ряды А и В сходятся 4) ряд А расходится, В сходится
17	Интервал сходимости ряда равен…	1) 2) 3) (-3;3) 4)
18	Третий член разложение функции в ряд Маклорена равен	А) Б) В) Г) 6

В зачетном задании должно быть отражено полное решение предложенных задач со всеми промежуточными выкладками и пояснениями (для выявления правильности понимания студентом материала). Если студент дает только ответ без решений, то задача считается не выполненной.

Зачетная работа должна быть оформлена аккуратно с ясным изложением решения. Объем работы не регламентируется.

По окончании написания зачетной работы и устранения студентом всех замечаний преподавателя предполагается ее защита в форме устного опроса.

! Студент, не выполнивший и не защитивший зачетную работу и не выполнивший программу дисциплины не получает зачет.